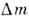 между ними определяет энергию связи системы:
между ними определяет энергию связи системы:
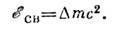
Связанное состояние - состояние системы частиц, при к-ром относит. движение частиц происходит в ограниченной области пространства (является финитным) в течение длит. времени по сравнению с характерными для данной системы периодами. Природа изобилует связанными состояниями: от звёздных скоплений и макроскопич. тел до микрообъектов - молекул, атомов, атомных ядер. Связанные состояния являются и многие из т. н. элементарных частиц (см. Кварки).
Для образования связанных состояний необходимо наличие сил притяжения по крайней мере
между нек-рыми частицами системы на нек-рых расстояниях между ними. Для
связанных состояний масса системы меньше суммы масс составляющих её частиц; разность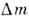 между ними определяет энергию связи системы:
между ними определяет энергию связи системы:
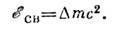
В классической механике связанными состояниями описываются финитными решениями ур-ний движения системы, траектории всех частиц системы сосредоточены в ограниченной области пространства. Примером может служить задача Кеплера о движении частицы (или планеты) в поле тяготения. В классич. механике система из двух притягивающихся частиц всегда может образовать связанные состояния. Если область расстояний, на к-рых частицы притягиваются, отделена энергетич. барьером (потенциальным барьером) от области, в к-рой они отталкиваются, то частицы также могут образовывать стабильные связанные состояния.
В квантовой механике, в отличие от классической, для образования связанных состояний
частиц необходимо, чтобы потенциальная энергия притяжения и радиус действия
сил были достаточно велики (см. Потенциальная яма, Нулевая энергия). Кроме того, в потенциальной яме типа изображённой на рис. из-за возможности
вылета частиц из области притяжения вследствие туннельного эффекта
не образуется стабильных связанных состояний, если энергия частицы больше потенциала на
бесконечности. Однако, если вероятность туннельного перехода мала (в классич.
пределе она равна нулю), то частица в такой потенциальной яме может находиться
достаточно длительное время (по сравнению с периодами движения в яме).
Поэтому наряду со стабильными связанными состояниями существуют нестабильные (метастабильные,
или квазистабильные) связанные состояния, к-рые с течением времени распадаются. Напр.,
нестабильными связанными состояниями по отношению к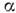 -распаду или (и) делению являются ядра нек-рых тяжёлых элементов.
-распаду или (и) делению являются ядра нек-рых тяжёлых элементов.
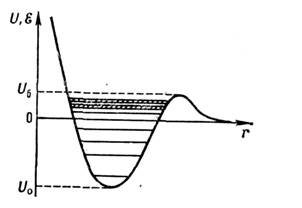
Зависимость потенциальной энергии U от расстояния r между частицами.
Стабильные связанные состояния лежат в области энергий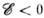 , им соответствуют дискретные уровни энергии системы. При
, им соответствуют дискретные уровни энергии системы. При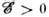 стабильные связанные состояния не существуют, однако в области
стабильные связанные состояния не существуют, однако в области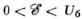 ,
где Uб - высота потенциального барьера, при некоторых
,
где Uб - высота потенциального барьера, при некоторых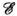 могут существовать квазистабильные связанные состояния, время жизни которых
определяется вероятностью туннельного перехода через потенциальный барьер
и может быть (особенно для частиц большой массы) весьма велико. Для макроскопических
тел связанные состояния могут иметь любую энергию в области
могут существовать квазистабильные связанные состояния, время жизни которых
определяется вероятностью туннельного перехода через потенциальный барьер
и может быть (особенно для частиц большой массы) весьма велико. Для макроскопических
тел связанные состояния могут иметь любую энергию в области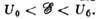
В крайне релятивистском случае, когда энергия связи системы сравнима с энергией покоя частиц системы, решение задачи связанных состояний требует привлечения квантовой теории поля (КТП). Точного решения такой задачи в совр. КТП не существует; нек-рые из развиваемых приближённых методов позволяют одинаковым образом рассматривать как стабильные «элементарные» частицы, так и нестабильные, включая резонансы.

В. Я. Файнберг
|
|