Плавных возмущений метод (метод Рытова) - приближённый метод решения волнового уравнения или Леонтовича
параболического уравнения, описывающего распространение волн с учётом
дифракции в среде с крупномасштабными (по сравнению с длиной волны)
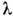неоднородностями показателя преломления; одна из разновидностей метода
возмущений. Предложен С. М. Рытовым в 1937 для решения задачи о дифракции
света на УЗ-волне. В дальнейшем П. в. м. применялся в разл. статистич.
задачах распространения волн в статистически неоднородных средах (напр.,
распространение радиоволн, света и звука в турбулентной атмосфере). Суть
П. в. м. состоит в том, что теория возмущений строится не для комплексной
амплитуды волны, а для комплексной фазы волны, что соответствует частичному
суммированию рядов теории возмущений, т. е. определённому учёту многократного
рассеяния волн.
Ур-ние П. в. м. для комплексной фазы Ф,
получаемое из параболич. ур-ния, имеет вид
Решение ищут в виде ряда Ф = Ф1
+ Ф2 + ..., представляющего собой разложение по степеням
В результате получается система ур-ний последоват. приближений:
Граничные условия для Фl
имеют один и тот же вид:
Решение любого из ур-ний можно представить
в виде
где К - Грина функция линейного
дифференциального оператора
описывающего дифракцию волн во френелевском приближении. На практике удаётся
вычислить лишь неск. первых членов Фl, обычно используют
только Ф1. Условие применимости П. в. м. требует достаточной
плавности изменения Ф1, отсюда и происходит название.
Литература по
Татарский В. И., Распространение волн в турбулентной атмосфере, М., 1967; Введение в статистическую радиофизику,
ч. 2 - Рытов С. М., Кравцов Ю. А., Татарский В. И., Случайные поля, М.,
1978; Исимару А., Распространение и рассеяние волн в случайно-неоднородных
средах, пер. с англ., т. 2, М., 1981.
Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.
)
неоднородностями показателя преломления; одна из разновидностей метода
возмущений. Предложен С. М. Рытовым в 1937 для решения задачи о дифракции
света на УЗ-волне. В дальнейшем П. в. м. применялся в разл. статистич.
задачах распространения волн в статистически неоднородных средах (напр.,
распространение радиоволн, света и звука в турбулентной атмосфере). Суть
П. в. м. состоит в том, что теория возмущений строится не для комплексной
амплитуды волны, а для комплексной фазы волны, что соответствует частичному
суммированию рядов теории возмущений, т. е. определённому учёту многократного
рассеяния волн.
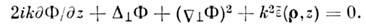
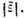В результате получается система ур-ний последоват. приближений:
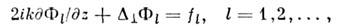
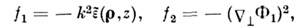
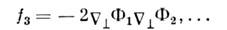
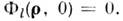
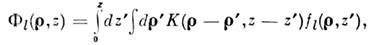
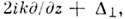описывающего 
