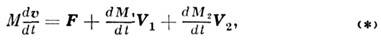
Механика тел переменной массы - раздел теоретич. механики, изучающий движение материальных
тел, масса к-рых изменяется во время движения. Осн. исследования по
механике тел переменной массы принадлежат И. В. Мещерскому и К. Э. Циолковскому. Задачи M. т. п. м. возникли
в связи с развитием авиационной и ракетной техники, а также теоретич. механики
и астрономии. Частной задачей механики тел переменной массы является движение тел с пост, массой,
но перем. моментом инерции. Изменение массы тела (точки) во время движения может
обусловливаться отделением (отбрасыванием) частиц или их присоединением (налипанием).
При полёте совр. реактивных самолётов с воздушно-реактивными двигателями происходят
одноврем. процессы как присоединения, так и отделения частиц. Масса таких самолетов
увеличивается за счёт воздуха, засасываемого в двигатель, и уменьшается в результате
отбрасывания продуктов горения топлива. Осн. векторное дифференц. ур-ние движения
точки перем. массы для случая присоединения и отделения частиц, полученное в
1904 Мещерским, имеет вид
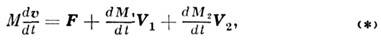
где M - масса точки, 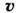 -
её скорость, t - время,
-
её скорость, t - время, 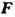 - равнодействующая приложенных сил,
- равнодействующая приложенных сил,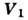 -
относит, скорость отделяющихся частиц,
-
относит, скорость отделяющихся частиц, -
секундный расход массы,
-
секундный расход массы,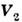 -
относит, скорость присоединяющихся частиц,
-
относит, скорость присоединяющихся частиц,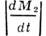 -
секундный приход массы. Произведение
-
секундный приход массы. Произведение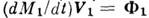 -
реактивная тяга, а
-
реактивная тяга, а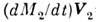 =
= - тормозящая сила, обусловленная присоединением частиц. Для совр. ракет ур-ние
движения получается из (*) при условии, что
- тормозящая сила, обусловленная присоединением частиц. Для совр. ракет ур-ние
движения получается из (*) при условии, что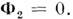
В механике тел переменной массы рассматриваются два класса задач:
определение траектории центра масс и определение движения тела перем. массы
около центра масс. В ряде случаев можно найти траекторные характеристики движения
центра масс, исходя из ур-ний динамики точки перем. массы. Изучение движения
тел перем. массы около центра масс важно для исследования динамич. устойчивости
реальных объектов (ракет, самолётов), их управляемости и манёвренности. К задачам
механике тел переменной массы относится также отыскание оптим. режимов движения, т. е. определение
таких законов изменения массы тела или точки, при к-рых кинематич. или динамич.
характеристики их движения становятся наилучшими. Наиб, эфф. методы решения
таких задач - методы вариационного исчисления.
Важной задачей механики тел переменной массы с твёрдой оболочкой
является изучение движения этих тел при нек-рых дополнит, условиях, налагаемых
на скорость центра масс. Такие задачи возникают, напр., при изучении движения
телеуправляемых ракет и беспилотных самолётов, наводимых на цель автоматически
или по радиокомандам с Земли, или по командам, вырабатываемым головками самонаведения.
Для зенитных управляемых ракет и ракет класса "воздух - воздух"
(предназначенных для стрельбы с самолёта по самолёту) процесс изменения массы
происходит, как правило, на всей траектории полёта.
Большое число работ по механике тел переменной массы относится к изучению движения небесных тел. Допуская, что увеличение массы небесного тела происходит за счёт налипания космич. пыли, приходят к дополнит, условию о равенстве нулю абс. скорости налипающих частиц. Ур-ние движения точки перем. массы в этом случае принимает вид
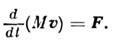
Интерполируя реальные законы изменения массы
небесных тел простыми алгебраич. функциями времени ("законы Мещерского"),
можно аналитически исследовать движение точки перем. массы в поле центральной
силы. Мещерскому принадлежит постановка обратных задач
механике тел переменной массы, в к-рых определяется закон изменения массы точки по нек-рым заданным
свойствам наблюдаемого движения в известном поле сил.
Для нек-рых задач небесной механики Мещерский указал такие преобразования переменных (координат и времени), при помощи которых уравнения точки переменной массы переходят в уравнения точки пост, массы (в новом пространстве-времени). Механика тел переменной массы находит приложение при исследованиях и в др. областях, напр, в текстильной промышленности и радиолокации.

А. А. Космодемьянский
Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.
В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.
|
|