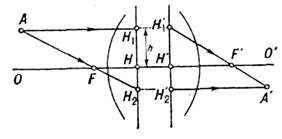
Кардинальные точки оптической системы - точки на оси ОО' (рис.) центрированной оптич. системы, позволяющие строить изображение произвольной точки пространства объектов в параксиальной области (вблизи оптич. оси).

В общем случае (за исключением телескопич. систем) за К. т. о. с. принимают след. 4 точки: передний F и задний F' фокусы, переднюю Н и заднюю Н' гл. точки. Задний фокус является изображением бесконечно удалённой точки, расположенной на оптич. оси в пространстве объектов, а передний фокус - изображением в пространстве объектов бесконечно удалённой точки пространства изображений. Главные точки яиляются точками пересечения с оптич. осью гл. плоскостей - сопряжённых плоскостей, для которых линейное увеличение равно 1, т. е. всякая точка H1 расположенная в гл. плоскости Н1Н2 на расстоянии h от оси, изображается в другой гл. плоскости H'1H'2 в точке Н'1 на том же расстоянии h от оси, что и точка Н1. Расстояние от точки Н до точки F наз. передним фокусным расстоянием (отрицательным на рис.), а расстояние от точки Н' до точки F' - задним фокусным расстоянием (положительным на рис.). С помощью перечисленных четырёх точек F, H, F' и Н' изображение произвольной точки А, создаваемое оптич. системой, можно построить след. образом: из точки А проводят 2 луча AH1 и AFH2. Первый луч, идущий параллельно оптич. оси и пересекающий заднюю гл. плоскость на расстоянии Н'H'1 от оси (Н-Н'1=НН1), проходит через задний фокус F'. Второй луч, проходящий через передний фокус F и переднюю гл. плоскость H1H2 в точке Н2, выходит из системы параллельно оси на расстоянии Н-Н'2 от оси (Н-Н'2=НН2). Точка пересечения А' этих двух лучей является изображением точки А, даваемым рассматриваемой оптпч. системой. Любой параксиальный луч, исходящий из точки А, по выходе из системы проходит через точку А'. Число К. т. о. с. в общем случае равно четырём. В нек-рых частных случаях их число уменьшается; напр., в бесконечно тонкой линзе или в системе из бесконечно тонких линз, разделённых бесконечно малыми воздушными промежутками, обе гл. плоскости сливаются в одну. Оптич. системы, содержащие одну отражающую поверхность, обладают только одной гл. плоскостью и одним фокусом, т. к. лучи, падающие на систему, могут распространяться только в одном направлении (навстречу отражающей поверхности). У телескопич. системы К. т. о. с. находятся на бесконечности, и поэтому построение изображения с их помощью невозможно. В этом случае можно разбить телескопич. систему на 2 части любым способом (напр., на объектив и окуляр) и построить изображение любой точки пространства объектов в отдельности для каждой части. В качестве К. т. о. с. не обязательно пользоваться фокусами и гл. точками, иногда последние заменяют узловыми точками, обладающими тем свойством, что луч, проходящий через переднюю узловую точку и образующий с осью угол a, после преломления проходит через заднюю узловую точку и образует с осью тот же угол а. Если значения показателей преломления первой и последней сред одинаковы, то узловые точки совпадают с главными. Иногда в качестве К. т. о. с. пользуются гл. точками и "антиглавными" точками - под последними понимают пару сопряжённых точек, для к-рых поперечное увеличение (см. Увеличение оптическое)равно -1. Можно также пользоваться узловыми и "антиузловыми" точками - парой сопряжённых точек, для к-рых угл. увеличение равно - 1. Построение изображения по перечисленным К. т. о. с. не представляет затруднений. Вообще говоря, в качестве К. т. о. с. можно принять 2 произвольно выбранные пары сопряжённых точек при условии, что известно линейное или угл. увеличение, соответствующее этим парам. Однако применение таких К. т. о. с. малоудобно и не получило распространения на практике.

Г. Г. Слюсарев
|
|