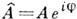 , где А
и j - вещественная амплитуда и фаза волны. Согласно принципу
суперпозиции, комплексная амплитуда результирующего поля просто равна
сумме таковых у отд. слагаемых (
, где А
и j - вещественная амплитуда и фаза волны. Согласно принципу
суперпозиции, комплексная амплитуда результирующего поля просто равна
сумме таковых у отд. слагаемых (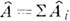 ), а для интенсивности волны А2 в случае двух волн с амплитудами
), а для интенсивности волны А2 в случае двух волн с амплитудами 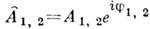 имеем
A2=A21+A22+2A1A2соsDj, (1)
где Dj=j2-j1. Величины А1,2, j1,2
в (1) в общем случае являются нек-рыми функциями координат и времени, вид
к-рых определяется конкретной структурой интерферирующих воли (напр.,
они зависят от расстоянии до соответствующих источников и их фаз). В
результате в тех точках, где Dj=m.2p, где m=0, b1, b2, . . ., А=А1+А2, а интенсивность А2 принимает макс, значение, превышающее сумму интенсивностей налагаемых волн. В точках же, где Dj=(m+1/2)2p, имеет место интерференц. минимум: А=|А1- A2|. В частном случае А1=А2
в этих точках суммарная амплитуда равна нулю, иными словами,
интерферирующие волны полностью "гасят" друг друга.
В трёхмерном пространстве геом. места точек максимумов и минимумов,
соответствующих определ. "порядкам" m, представляют собой нек-рые
поверхности, пересечение к-рых с произвольной плоскостью наблюдения
(экрана) даёт т. н. интерференц. полосы. Напр., в случае двух плоских
волн с фазами j1=-k1r+j01, j2=-k2r+j02 (где k1,2 - волновые векторы, j01, j02 - нач. фазы, определяемые фазами колебаний источников, k1=k2=2p/l) имеем: Dj=-Dkr+j02-j01. где Dk=k2-k1
и поверхности максимумов и минимумов будут представлять собой
плоскости, перпендикулярные вектору Dk; при этом расстояние между
соседними максимумами равно l[2sin(a/2)]-1, где l - длина волны, a=|Dk|/k - угол между векторами k1 и k2. Предельный случай a=p и А1=А2 соответствует стоячей волне, он может быть реализован, напр., при полном отражении бегущей плоской волны от нек-рой плоскости, перпендикулярной направлению её распространения.
имеем
A2=A21+A22+2A1A2соsDj, (1)
где Dj=j2-j1. Величины А1,2, j1,2
в (1) в общем случае являются нек-рыми функциями координат и времени, вид
к-рых определяется конкретной структурой интерферирующих воли (напр.,
они зависят от расстоянии до соответствующих источников и их фаз). В
результате в тех точках, где Dj=m.2p, где m=0, b1, b2, . . ., А=А1+А2, а интенсивность А2 принимает макс, значение, превышающее сумму интенсивностей налагаемых волн. В точках же, где Dj=(m+1/2)2p, имеет место интерференц. минимум: А=|А1- A2|. В частном случае А1=А2
в этих точках суммарная амплитуда равна нулю, иными словами,
интерферирующие волны полностью "гасят" друг друга.
В трёхмерном пространстве геом. места точек максимумов и минимумов,
соответствующих определ. "порядкам" m, представляют собой нек-рые
поверхности, пересечение к-рых с произвольной плоскостью наблюдения
(экрана) даёт т. н. интерференц. полосы. Напр., в случае двух плоских
волн с фазами j1=-k1r+j01, j2=-k2r+j02 (где k1,2 - волновые векторы, j01, j02 - нач. фазы, определяемые фазами колебаний источников, k1=k2=2p/l) имеем: Dj=-Dkr+j02-j01. где Dk=k2-k1
и поверхности максимумов и минимумов будут представлять собой
плоскости, перпендикулярные вектору Dk; при этом расстояние между
соседними максимумами равно l[2sin(a/2)]-1, где l - длина волны, a=|Dk|/k - угол между векторами k1 и k2. Предельный случай a=p и А1=А2 соответствует стоячей волне, он может быть реализован, напр., при полном отражении бегущей плоской волны от нек-рой плоскости, перпендикулярной направлению её распространения.
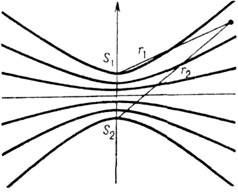
Рис. 1. Интерференция волн от двух точечных источников. Др. характерный пример - интерференция двух сферич. волн, исходящих из соответствующих центров S1 и S2 (рис. 1), разнесённых на нек-рое расстояние d=S1S2. В этом случае Dj=-kD+j02-j01 (где D=r2-r1 - разность хода, r1,2 - расстояния от источников до точки наблюдения) и максимумы так же, как и минимумы между ними, располагаются на гиперболоидах вращения вокруг оси S1S2, а в плоскости, параллельной этой оси, интерференц. полосы имеют вид гипербол. Общее число максимумов здесь определяется из условия |m|[d/l,. Аналогичным образом можно рассмотреть и др. случаи-интерференцию цилиндрич. волн, интерференцию от неск. источников (рис. 2 и 3) и др. С точки зрения энергетич. соотношений образование интерференц. максимумов и минимумов означает перераспределение потока энергии в пространстве - если, напр., отд. источники изотропны (равномерно излучают во все стороны), то неск. таких источников дают уже более сложную "изрезанную" диаграмму направленности А2=А21+А22+2А1А2соsDj, (1) Особым является случай малого расстояния между источниками (d[l/2); здесь при заданных значениях "парциальных" амплитуд волн A1,2 в зависимости от разности j02-j01 изменяется и суммарная мощность излучения, иными словами, источники волн непосредственно влияют друг на друга. В реальной ситуации при

Рис. 2. Вид интерференционных полос в случае двух сферических волн. этом сами амплитуды Al,2 зависят от способа возбуждения источников, напр, для двух близко расположенных электрич. диполей значения амплитуд излучаемых волн и полной мощности излучения оказываются различными в зависимости от того, что считать заданным - токи или напряжения. В случае векторных волн выражение (1) остаётся в силе, если в интерференц. члене под А1А2 понимать

Рис. 3. Интерференционные полосы в случае сферической и плоской волн. скалярное произведение соответствующих векторов. Для существования интерференц. эффекта здесь необходимо, чтобы векторы А1,2 (напр., напряжённости электрич. поля в эл--магн. волне) не были ортогональны друг к другу. Поверхности максимумов и минимумов (и соответствующие им интерференц. полосы на экране) неподвижны, если разность фаз Dj и, строго говоря, также амплитуды A1,2 в (1) неизменны во времени. В случае независимых источников, напр., небольшая расстройка между их частотами Dw=w2-w1 эквивалентна монотонному уходу разности фаз: Dj=Dwt, при этом координаты максимумов и минимумов будут перемещаться в пространстве, а в заданной точке амплитуда будет испытывать биения с разностной частотой Dw: от А1+А2 до |А1- A2|. Такие же биения, но нерегулярные во времени, возникают из-за фазовых нестабильностей источников, если случайные уходы разности фаз порядка или больше p. Возможность наблюдения интерференц. максимумов и минимумов при этом зависит от степени инерционности регистрирующей аппаратуры - любой прибор, строго говоря, проводит усреднения по нек-рому времени t0. Если t0 мало по сравнению с характерным периодом биений результирующего поля ("времени когерентности" t, к-рое порядка обратной ширины спектра волны), то обусловленные интерференц. членом в (1) максимумы и минимумы будут зарегистрированы и в случае независимых источников. По мере роста отношения t0/t, вследствие случайных изменений cosDj(t), происходит постепенное сглаживание ("размывание") интерференц. максимумов и минимумов, а при t0дt И. в. не наблюдается - измеряемая интенсивность А2 результирующего поля будет равна сумме ннтенсивностей составляющих волн. В случае типичных генераторов радиоволн, напр., легко достигается не только условие t0Ъt, но и более сильное неравенство t0Ъ2p/w, поэтому наблюдение И. в. от независимых источников не представляет трудностей. В оптике же для "естеств." источников квазимонохроматич. света (даже отд. спектральных линий теплового излучения газов) ситуация существенно иная - здесь при нормальных условиях значение t~10-9-10-10 с, тогда как для человеческого глаза t0~10-1 с, для скоростных фотокинокамер t0/10-7 с. Поэтому долгое время интерференцию в оптике удавалось наблюдать лишь в случае когерентных волн (см. Когерентность ),получаемых путём разделения излучения от к--л. одного источника. При этом для небольших разностей хода между интерферирующими лучами случайные уходы фаз j1(t) и j2(t) оказываются одинаковыми и разность фаз Dj от времени почти не зависит (о конкретных схемах разделения см. Интерференция света ).Благодаря появлению источников высококогерентного света - лазеров стало возможным наблюдать интерференцию от независимых источников и в оптич. диапазоне, поскольку время их когерентности может достигать 10-2 с и более, а также в результате разработки малоинерц. фотоэлектронных устройств с t0[10-9с. Принцип суперпозиции перестаёт выполняться при распространении волн достаточно большой интенсивности в нелинейных средах; при этом имеют место качественные особенности (см. Волны, Нелинейная оптика, Нелинейная, акустика). Явление И. в. находит разнообразное применение. Для её осуществления разработаны разл. схемы интерферометров (как двух-, так и многолучевых). Тот факт, что расположение интерференц. полос зависит от длины волны и разности хода лучей, позволяет по виду интерференц. картины (или их смещению) проводить точные измерения расстояний при известной длине волны или, наоборот, определять спектр интерферирующих волн. Кроме того, по интерференц. картине можно выявлять и измерять неоднородности среды (в т. ч. фазовые), в к-рой распространяются волны в одном из плеч интерферометра, или отклонения формы поверхности от заданной. Явление И. в., рассеянных от нек-рого объекта (или прошедших через него), с "опорной" волной лежит в основе голографии (в т. ч. оптич., акустич. или СВЧ-голографии). И. в. от отд. "элементарных" излучателей используется при создании сложных излучающих систем (антенн)для эл--магн. и акустич. волн.

