Анизотропия твёрдых тел (от греч.
anisos - неравный и tropos - направление) - зависимость равновесных физ. свойств
твёрдого тела от направления (см. Анизотропная среда ).Величины, описывающие
макроскопич. свойства вещества, делятся на скаляры, псевдоскаляры, векторы и
тензоры разл. рангов. Скалярная характеристика (напр., ср. плотность вещества,
темп-pa, теплоёмкость, энтропия) задаётся одним числовым значением, к-рое не
связано с понятием направления в пространстве и не изменяется при вращении.
Подобная характеристика однородного тела в состоянии равновесия не может обладать
А. Псевдоскалярные характеристики, напр. уд. вращение плоскости поляризации,
также изотропны, т. к. их численное значение сохраняется при поворотах тела
или системы координат (но они меняют знак при отражении). Для задания векторной
величины (напр., ср. намагниченности кристалла) требуется указать 3 компонента
вектора в нек-рой системе координат. Эти компоненты являются проекциями вектора
на оси координат, они изменяются при вращении системы координат.
Примером физ. свойств, описываемых симметричными
тензорами 2-го ранга, могут служить электропроводность и теплопроводность, а
также диэлектрич. и магн. проницаемости твёрдых тел. В общем случае в нек-рой
системе координат тензор 2-го ранга имеет 9 компонент. Если тензор симметричен,
то независимыми являются лишь 6 из них - три диагональных и три недиагональных
элемента матрицы. При повороте системы координат матрица тензора преобразуется
по определ. закону. Всякий симметричный тензор 2-го ранга может быть приведён
к гл. осям, т. е. существует такая система координат, в к-рой матрица этого
тензора диагональна; соответствующие 3 диагональных элемента наз. гл. значениями
тензора. Если гл. значения не совпадают, имеет место А., а направления гл. осей
определены однозначно.

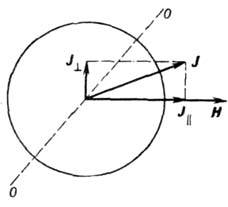
Исследуемый образец (диск) в магнитном
поле.
Так, для кристаллов (кроме кубических)
направление электрич. тока обычно не совпадает с направлением приложенного электрич.
поля. Если, однако, поле приложено вдоль одной из гл. осей кристалла, возникающий
ток будет параллельным полю и, измеряя значения проводимости вдоль трёх гл.
осей, можно определить гл. значения тензора электропроводности кристалла. Аналогично
могут быть определены гл. значения тензоров теплопроводности, диэлектрич. и
магн. проницаемостей. Если для тензора два гл. значения совпадают, говорят,
что в отношении данной тензорной характеристики вещество является одноосным;
вещество с несовпадающими тремя гл. значениями наз. двухосным. Если все три
гл. значения симметричного тензора 2-го ранга одинаковы, матрица тензора диаго-нальна
во всякой системе координат и не изменяется при вращениях системы координат.
В этом важном частном случае для задания тензорной характеристики достаточно
указать всего одну величину. Это означает, что в отношении данной характеристики
вещество изотропно.
Вещество может обладать и более сложными
тензорными характеристиками. Так, коэф. пьезоэлектрич. эффекта (см. Пьезоэлектричество)образуют тензор 3-го ранга, а характеристики упругих свойств вещества образуют
тензор упругих модулей 4-го ранга, для задания к-рого в произвольной системе
координат необходимо указать значения 34=81 его элементов. Учёт симметрии
позволяет, однако, значительно понизить число независимо задаваемых компонент.
А. кристаллов связана с симметрией их
кристаллич. структуры (см. Кюри, принцип, Неймана принцип, Симметрия кристаллов). Чтобы вещество обладало векторной характеристикой (напр., спонтанной поляризацией
в случае сегнетоэлектриков), его кристаллич. решётка не должна быть симметричной
относительно преобразования инверсии, т. е. не должна обладать центром симметрии.
Все кубич. кристаллы изотропны в отношении характеристик, описываемых симметричными
тензорами 2-го ранга (напр., электропроводности или
диэлектрич. проницаемости). Менее симметричные кристаллы
обладают А. в отношении этих свойств.
Тензорный характер диэлектрич. проницаемости
проявляется в , в частности,
в эффекте двойного лучепреломления для
некубич. прозрачных кристаллов. В табл.
приведено число независимых упругих постоянных
(число независимых элементов матрицы тензора упругих модулей) для кристаллов
разл. сингоний.
|
Кристаллическая сингония |
Число упругих постоянных |
|
Триклинная |
21 |
|
Моноклинная |
13 |
|
Ромбическая |
9 |
|
Тетрагональная |
7 или 6 |
|
Тригональная (ромбоэдрич ) |
6 |
|
Гексагональная |
5 |
|
Кубическая |
3 |
А. может быть искусственно вызвана внеш.
воздействием. Поликристаллич. материалы, состоящие из огромного числа случайно
ориентированных мелких монокристаллов, могут приобрести А. в результате механич.
обработки, напр. прокатки (см. Текстура ).Искусственная оптич. А. может
быть создана в кристаллах и изотропных средах под действием внеш. электрич.
(см. Керра эффект)или магн. (см. Коттона-Мутона эффект)поля
либо путём механич. воздействия (см. Фотоупругость).

|
|