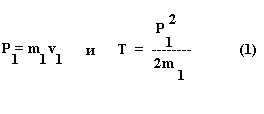
Наши многочисленные лабораторные опыты показали, что у времени помимо пассивного свойства длительности существуют еще и активные свойства: направленность хода и плотность, определяющая степень его активности. В результате время не только открывает возмож ности для развития процессов, но как некоторая физическая реальность может воздействовать на них и на состояние вещества. При этом происходит взаимодействие, ведущее к тому, что и сама плотность времени будет изменяться под воздействием происходящих вбли зи процессов. Через это изменение свойств времени может осуществляться связь между процессами. Время непрерывным потоком входит в наш Мир, и если оно обладает активными физическими свойствами, то будет единственным явлением природы, идущим против хода вс ех событий. Действительно, к настоящему все приходит от прошлого, и только время входит от будущего в настоящее. Обычный ход процессов ведет к возрастанию энтропии системы. Поэтому обратное действие активных свойств времени должно вносить в Мир жизненное начало, противодействующее обычной тенденции разрушения и смерти. Опыт показывает, что вблизи процессов, повышающих плотность времени, действительно возрастает организованность вещества. Но для такой перестройки требуются механические действия. Поэтому должно наблюдаться не только физическое, но и механическое изменение в веществе как в сложном ансамбле, подчиняющемся закономерностям статистической механики, когда под действием некоторой причины в нем происходят необратимые процессы возрастания энтропии. Чтобы выяснить сущность этих механических изменений, рассмотрим простейшую схему с необратимыми явлениями, которые должны возникнуть при абсолютно неупругом соударении тел. Допустим, что соударяются два тела с массами m_1 и m_2, которые движутся со скоростями v_1 и v_2. Будем пользоваться инерциальной системой координат, относительно которой одно из этих тел неподвижно. Пусть это будет второе тело, и, значит, v_2 = 0. Тогда до удара общий импульс системы Р и ее кинетическая энеггия T будут определяться их значениями для первого тела:
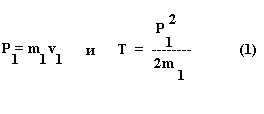
После неупругого удара тела приобретают общую скорость. Согласно закону сохранения импульса по-прежнем
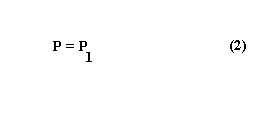
Кинетическая же энергия объединенных тел Т будет иной. Обозначим через М их общую массу. Тогда
Отсюда согласно (1) и (2) находим
значит, Т<Т_1, и, следовательно, неупругий удар возможен только в том случае, когда происходит процесс перестройки структуры тел, поглощающий их механическую энергию. В этом явлении, сочетающем механику с термодинамикой, увеличивается энтропия системы. Процесс же перестройки внутренней структуры тел должен развиваться не только во времени, но и при активном его участии. При этом будет оставаться в силе закон сохранения импульса, так как он основан на самых общих свойствах причинности, из которых следуе т, что при любых изменениях причинных связей должно соблюдаться равенство действия и противодействия, а значит, и компенсация всех внутренних сил системы. Иными словами, время не несет импульса и не может нарушать полного импульса системы. Поэтому, каков а бы ни была роль времени, кинетическая энергия после удара будет определяться тем же выражением (4), как и в классическом случае обычного, не активного времени, поскольку его вывод основан только на законе сохранения импульса. Активность времени препятствует диссипации энергии и посту энтропии. Поэтому механическая, т. е. кинетическая, энергия системы должна оказаться больше того значения, которое следует из формулы (4) при М="(m_1" + m_2). Но, как следует из этой формулы, увели чение Т возможно только в том случае, если в процессе объединения тел происходит уменьшение их общей массы:
Этот вывод с неизбежностью вытекает из активных свойств времени и закона сохранения импульса. Если он будет подтвержден опытом, то окажется вторым после астрономических наблюдений мгновенности воздействий, решающим и особенно наглядным доказательством су ществования у времени активных свойств. Разумеется, уменьшение массы происходит не за счет уменьшения количества вещества, а из-за уменьшения инертной массы, т. е. коэффициента при ускорении во втором законе Ньютона. Время входит в этот закон, и поэтому величина коэффициента может зависеть от его свойств. Сейчас важно отметить только эту принципиальную возможность, и если опыты ее подтвердят, то на их основе можно будет исследовать и механизм явления. Согласно принципу эквивалентности Эйнштейна гравитационная и инертная массы должны быть тождественны друг другу. Поэтому при упругом ударе должно происходить и уменьшение веса Q в соответствии с выражением Q=Mg. Это заключение позволяет осуществить простую экспериментальную проверку сравнением веса тела до и после удара. Следует еще отметить, что из-за уменьшения веса тела, т. е. действия Земли на него, не нарушается сохранение импульса, поскольку при этом на ту же величину уменьшается действие тела на Землю. Уже первые опыты показали, что при ударе тел с необратимой деформацией действительно происходит уменьшение их веса. На аналитических весах с ценой деления 1,4 мг производилось взвешивание тел весом до 200 г - предела нормальной работы этих весов. Для контроля и взвешивания тяжелых тел до 1 кг применялись еще и технические весы первого класса с ценой деления, равной 10 мг. При этих опытах оказалось, что уменьшение веса не исчезает сразу по окончании процесса соударения, а остается, убывая постепенно со временем релаксации порядка 15-20 мин. Это чрезвычайно важное обстоятельство существенно упрощает опыты: остается достаточно времени для тщательного взвешивания, и получается возможность наблюдать постепенное восстановление веса. В дальнейших опытах взвешивалось жесткое упругое тело (шарикоподшипник) после удара о неупругую плиту (свинец) и, наоборот, взвешивался свинец после удара о жесткое основание (каменный пол). Затем были проведены опыты взвешивания деформируемой коробки по сле многих резких сотрясений находившихся в ней жестких тел и, наоборот, взвешивание свинцовой дроби после ударов в жесткой коробке. Определялся вес коробки со всем, что в ней было, а также раздельно: вес коробки и вес ее содержимого. Эти опыты показали, что облегчается только то тело, в котором происходит процесс необратимой деформации. Такой результат и следовало ожидать из общих теоретических соображений, согласно которым лишь в необратимых процессах обнаруживается отличие причин от следствий и, значит, течение времени с его активными свойствами. На рис. 1 в качестве типичного примера показан график облегчения веса жестяной коробки весом 108 г после многократных сотрясений находившихся в ней небольших стальных шариков.
Рис. 1. Уменьшение веса тела в результате неупругого удара и его постепенное восстановление. Технические весы с демпфером. Уменьшение веса дано на оси ординат в миллиграммах. а по оси абсцисс отложено время взвешивания, отсчитанное от момента, когда происходило воздействие на коробку.
Восстановление веса, правда не совсем полное, происходило здесь и в других опытах за время порядка двадцати минут. Остающееся же небольшое отличие от первичного веса исчезает лишь по прошествии десятка часов. Полное восстановление показаний весов дает контроль чистоты эксперимента и показывает реальность наблюдавшейся потери веса. Задержка облегченного состояния тела вызвана, вероятно, тем, что увеличение веса и инертной массы должно приводить к возрастандовательно, для возвращения веса к норме требуется затрата дополнительной энергии. Благодаря дисперсии скоростей медленные части цы могут черпать эту энергию взаимодействием с частицами больших скоростей и таким путем восстанавливать свою массу. Происходящая от этого потеря общей тепловой энергии тела приведет к притоку тепла из окружающей обстановки и к постепенному восстановлени ю массы всех частиц тела. Необходимое для этого время должно быть несколько больше, хотя и сравнимо с временем тепловых релаксаций в теле, что и наблюдалось в действительности. Другая особенность восстановления веса заключается в асимптотическом приближе нии веса не к своему первоначальному, а к несколько уменьшенному значению, которое сохраняется значительно дольше времени ретаксации. Таким образом, кроме обычного состояния тела возможно еще и другое, почти устойчивое, с меньшей массой и весом. В принципе такая устойчивость возможна, если возвращение к большой массе само представляет собой процесс, который ведет к ее уменьшению. При соударении облегчение испытывает тело, в котором произошла необратимая деформация, и оно должно быть связано с физикой самой этой деформации. Поэтому эффект облегчения должен наблюдаться при любой необратимой деформации независимо от ее причины. Это заключение полностью подтверждает опыт. На рис. 2 представлена запись колебаний стрелки аналитических весов после того, как на их чашку был сразу же положен сильно смятый тонкий медный лист весом 40,2 г. Как видно из рисунка, начальный эффект облегчения листа достиг 6-7 мг с постепенным возвращением минут за 15 к его обычному весу, показанному нижней линией записи.
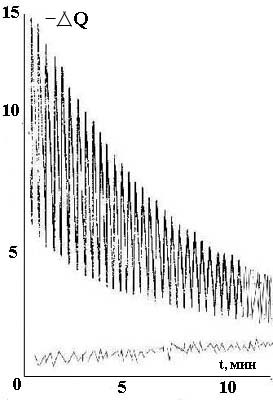
Рис. 2. Уменьшение веса в результате неупругой деформации тела и его восстановление. Весы аналитические.
В случае же обратимой деформации изменение веса тела не наблюдается. Так, сжатая резина или сжатая стальная пружина показывают свой обычный вес. Этот результат и следовало ожидать, поскольку при обратимых процессах (как при упругом ударе) не меняется энтропия системы. Поэтому уменьшение веса тел надо искать при процессах в них с большим возрастанием энтропии. Оказалось, что разогрев тел действительно приводит к очень значительному уменьшению их веса. Изучение этого явления принесло большой материал, позволяющий глубже проникнуть в понимание того, каким образом активные свойства времени вызывают уменьшение массы и веса тела.
|
|
 |
