
И.В.Черных
|
Назначение:
Выполняет вычисление абсолютного значения величины сигнала.
Параметры:
Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.
Пример использования блока Abs, вычисляющего модуль текущего значения синусоидального сигнала, показан на рис. 9.6.1.

Рис. 9.6.1. Пример использования блока Abs
Блок Abs может использоваться также для вычисления модуля сигнала комплексного типа. На рис. 9.6.2 показан пример вычисления модуля комплексного сигнала вида:
![]() .
.
Модуль этого сигнала (как и следовало ожидать) равен 1 для любого момента времени.
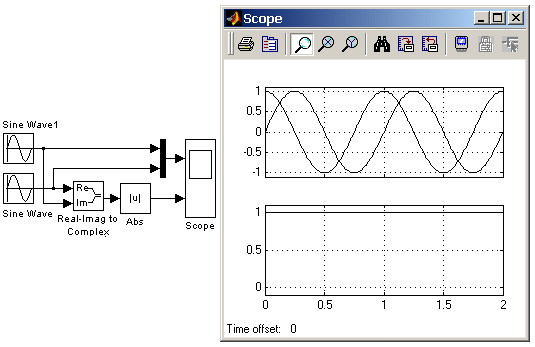
Рис. 9.6.2. Пример использования блока Abs для вычисления модуля комплексного сигнала
9.6.2. Блок вычисления суммы Sum
Назначение:
Выполняет вычисление суммы текущих значений сигналов.
Параметры:
Icon shape – Форма блока. Выбирается из списка.
- round – окружность,
- rectangular – прямоугольник.
List of sign – Список знаков. В списке можно использовать следующие знаки:
+ (плюс), - (минус) и | (разделитель знаков).
Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.
Количество входов и операция (сложение или вычитание) определяется списком знаков параметра List of sign, при этом метки входов обозначаются соответствующими знаками. В параметре List of sign можно также указать число входов блока. В этом случае все входы будут суммирующими.
Если количество входов блока превышает 3, то удобнее использовать блок Sum прямоугольной формы.
Блок может использоваться для суммирования скалярных, векторных или матричных сигналов. Типы суммируемых сигналов должны совпадать. Нельзя, например, подать на один и тот же суммирующий блок сигналы целого и действительного типов.
Если количество входов блока больше, чем один, то блок выполняет поэлементные операции над векторными и матричными сигналами. При этом количество элементов в матрице или векторе должно быть одинаковым.
Если в качестве списка знаков указать цифру 1 (один вход), то блок можно использовать для определения суммы элементов вектора.
Примеры использования блока Sum показаны на 9.6.3.
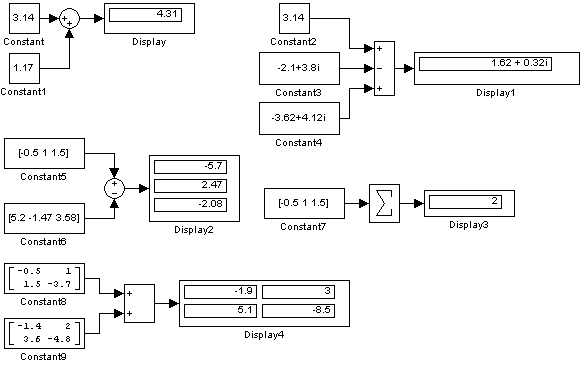
Рис. 9.6.3. Примеры использования блока Sum
9.6.3. Блок умножения Product
Назначение:
Выполняет вычисление произведения текущих значений сигналов.
Параметры:
Number of inputs – Количество входов. Может задаваться как число или как список знаков. В списке знаков можно использовать знаки * (умножить) и / (разделить).
Multiplication – Способ выполнения операции. Может принимать значения (из списка):
- Element-wise – Поэлементный.
- Matrix – Матричный.
Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.
Если параметр Number of inputs задан списком, включающим кроме знаков умножения также знаки деления, то метки входов будут обозначены символами соответствующих операций.
Блок может использоваться для операций умножения или деления скалярных векторных или матричных сигналов. Типы входных сигналов блока должны совпадать. Если в качестве количества входов указать цифру 1 (один вход), то блок можно использовать для определения произведения элементов вектора.
Примеры использования блока Product при выполнении скалярных и поэлементных операций показаны на 9.6.4.

Рис. 9.6.4. Примеры использования блока Product при выполнении скалярных и поэлементных операций
При выполнении матричных операций необходимо соблюдать правила их выполнения. Например, при умножении двух матриц необходимо, чтобы количество строк первой матрицы равнялось количеству столбцов второй матрицы. Примеры использования блока Product при выполнении матричных операций показаны на рис. 9.6.5. В примере показаны операции формирования обратной матрицы, деление матриц, а также умножение матриц.
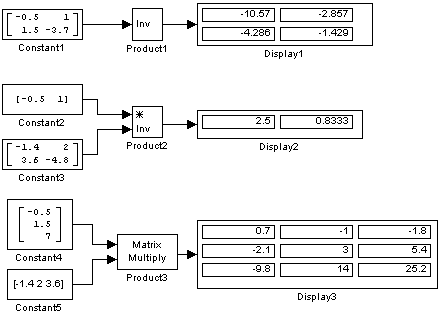
Рис. 9.6.5. Примеры использования блока Product при выполнении матричных операций
9.6.4. Блок определения знака сигнала Sign
Назначение:
Определяет знак входного сигнала.
Параметры:
Нет.
Блок работает в соответствии со следующим алгоритмом:
Если входной сигнал блока положителен, то выходной сигнал равен 1.
Если входной сигнал блока отрицателен, то выходной сигнал равен -1.
Если входной сигнал блока равен 0, то выходной сигнал также равен 0.
Рис. 9.6.6. иллюстрирует работу блока Sign.
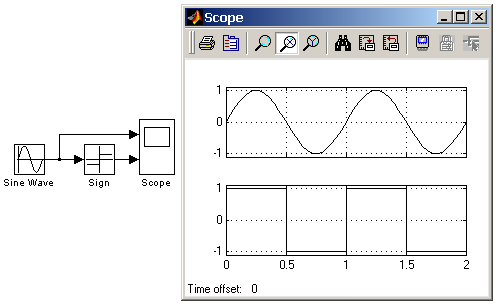
Рис. 9.6.6. Пример использования блока Sign
9.6.5. Усилители Gain и Matrix Gain
Назначение:
Выполняют умножение входного сигнала на постоянный коэффициент.
Параметры:
Gain – Коэффициент усиления.
Multiplication – Способ выполнения операции. Может принимать значения (из списка):
- Element-wise K*u– Поэлементный.
- Matrix K*u – Матричный. Коэффициент усиления является левосторонним операндом.
- Matrix u*K – Матричный. Коэффициент усиления является правосторонним операндом.
Saturate on integer overflow (флажок) – Подавлять переполнение целого. При установленном флажке ограничение сигналов целого типа выполняется корректно.
Блоки усилителей Gain и Matrix Gain есть один и тот же блок, но с разными начальными установками параметра Multiplication.
Параметр блока Gain может быть положительным или отрицательным числом, как больше, так и меньше 1. Коэффициент усиления можно задавать в виде скаляра, матрицы или вектора, а также в виде вычисляемого выражения.
В том случае если парметр Multiplication задан как Element-wise K*u, то блок выполняет операцию умножения на заданный коэффициент скалярного сигнала или каждого элемента векторного сигнала. В противном случае блок выполняет операцию матричного умножения сигнала на коэффициент заданный матрицей.
По умолчанию коэффициент усиления является действительным числом типа double.
Для операции поэлементного усиления входной сигнал может быть скалярным, векторным или матричным любого типа, за исключением логического (boolean). Элементы вектора должны иметь одинаковый тип сигнала. Выходной сигнал блока будет иметь тот же самый тип, что и входной сигнал. Параметр блока Gain может быть скаляром, вектором или матрицей либого типа, за исключением логического (boolean).
При вычислении выходного сигнала блок Gain использует следующие правила:
Если входной сигнал действительного типа, а коэффициент усиления комплексный, то выходной сигнал будет комплексным.
Если тип входного сигнала отличается от типа коэффициента усиления, то Simulink пытается выполнить приведение типа коэффициента усиления к типу входного сигнала. В том случае, если такое приведение невозможно, то расчет будет остановлен с выводом сообщения об ошибке. Такая ситуация может возникнуть, например, если входной сигнал есть беззнаковое целое (uint8), а параметр Gain задан отрицательным числом.
Примеры использования блока Gain при выполнении скалярных и поэлементных операций показаны на 9.6.7.
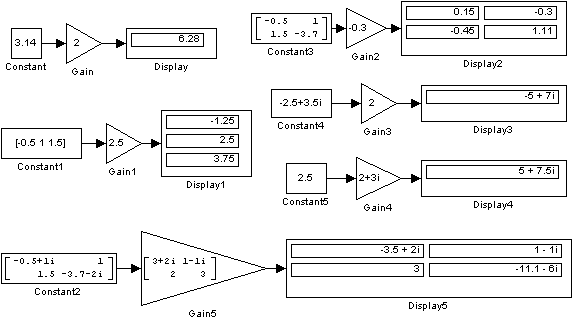
Рис. 9.6.7. Примеры использования блока Gain.
Для операций матричного усиления (матричного умножения входного сигнала на заданный коэффициент) входной сигнал и коэффициент усиления должны быть скалярными, векторными или матричными значениями комплексного или действительного типа single или double.
Примеры использования блока Matrix Gain при выполнении матричных операций показаны на рис. 9.6.8.
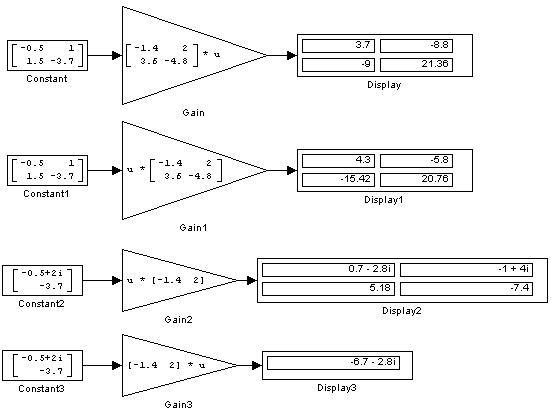
Рис. 9.6.8. Примеры использования блока Matrix Gain
9.6.6. Ползунковый регулятор Slider Gain
Назначение:
Обеспечивает изменение коэффициента усиления в процессе расчета.
Параметры:
Low – Нижний предел коэффициента усиления.
High – Верхний предел коэффициента усиления.
Для изменения коэффициента усиления блока Slider Gain необходимо передвинуть ползунок регулятора. Перемещение ползунка вправо приведет к увеличению коэффициента усиления, перемещение влево – к уменьшению. Изменение коэффициента усиления будет выполняться в пределах диапазона заданного параметрами Low и High.
Если щелкнуть с помощью мыши на левой или правой стрелках шкалы регулятора, то коэффициент усиления изменится на 1% от установленного диапазона. Если щелкнуть с помощью мыши на самой шкале регулятора слева или справа от ползунка, то коэффициент усиления изменится на 10% от установленного диапазона. Можно также просто задать требуемое значение коэффициента в среднем окне блока.
Блок может выполнять поэлементное усиление векторного или матричного сигнала. Входной сигнал может быть комплексным.
Примеры использования блока Slider Gain показаны на рис. 9.6.9.

Рис. 9.6.9. Примеры использования блока Slider Gain
9.6.7. Блок скалярного умножения Dot Product
Назначение:
Выполняет вычисление скалярного произведения (свертку) двух векторов.
Параметры:
Нет.
Блок выполняет вычисление выходного сигнала в соответствии с выражением: ![]() ,
,
где u1 и u2 – входные векторы,
conj – операция вычисления комплексно-сопряженного числа,
sum – операция вычисления суммы.
Если оба входных вектора являются действительными, то выходной сигнал также будет действительным. Если хотя бы один из входных векторов содержит комплексный сигнал, то выходной сигнал будет комплексным.
Примеры, иллюстрирующие работу блока Dot Product, показаны на рис. 9.6.10.
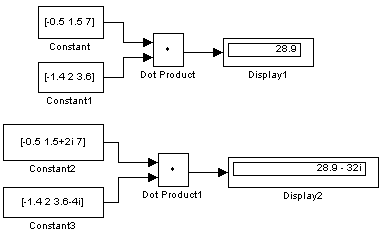
Рис. 9.6.10. Примеры использования блока Dot Product
9.6.8. Блок вычисления математических функций Math Function
Назначение:
Выполняет вычисление математической функции.
Параметры:
Function – Вид вычисляемой функции (выбирается из списка):
exp – Экспоненциальная функция
log – Функция натурального логарифма
10^u – Вычисление степени 10
log10 – Функции логарифма
magnitude^2 – Вычисление квадрата модуля входного сигнала
square – Вычисление квадрата входного сигнала
sqrt – Квадратный корень
pow – Возведение в степень
conj – Вычисление комплексно-сопряженного числа
reciprocal – Вычисление частного от деления входного сигнала на 1
hypot –Вычисление корня квадратного из суммы квадратов входных сигналов (гипотенузы прямоугольного треугольника по значениям катетов)
rem – Функция, вычисляющая остаток от деления первого входного сигнала на второй
mod – Функция, вычисляющая остаток от деления с учетом знака
transpose – Транспонирование матрицы
hermitian – Вычисление эрмитовой матрицы.
Output signal type – Тип выходного сигнала (выбирается из списка):
auto – Автоматическое определение типа
real –Действительный сигнал
complex- Комплексный сигнал.
Тип выходного сигнала в зависимости от типа входного сигнала, вычисляемой функции и параметра блока Output signal type приведен в таблице 9.6.1.
Таблица 9.6.1.
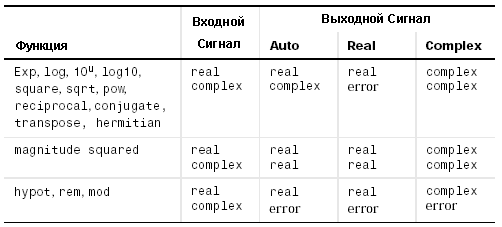
Примеры использования блока Math Function показаны на рис. 9.6.11.

Рис. 9.6.11. Примеры использования блока Math Function
9.6.9. Блок вычисления тригонометрических функций Trigonometric Function
Назначение:
Выполняет вычисление тригонометрической функции.
Параметры:
Function – Вид вычисляемой функции (выбирается из списка): sin, cos, tan, asin, acos, atan, atan2, sinh, cosh и tanh.
Output signal type – Тип выходного сигнала (выбирается из списка):
- auto – Автоматическое определение типа.
- real –Действительный сигнал.
- complex- Комплексный сигнал.
При векторном или матричном входном сигнале блок выполняет поэлементное вычисление заданной функции.
Примеры использования блока Trigonometric Function показаны на рис. 9.6.12.
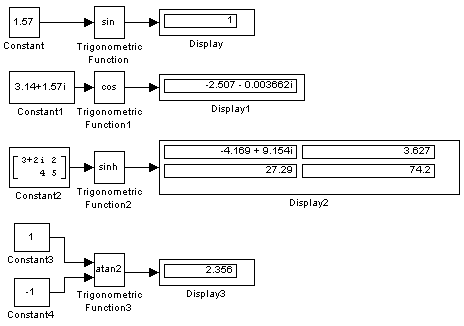
Рис. 9.6.12. Примеры использования блока Trigonometric Function
9.6.10. Блок вычисления действительной и (или) мнимой части комплексного числа Complex to Real-Imag
Назначение:
Вычисляет действительную и (или) мнимую часть комплексного числа.
Параметры:
Output – Выходной сигнал (выбирается из списка):
Real – Действительная часть
Image – Мнимая часть
RealAndImage – Действительная и мнимая часть.
Входной сигнал блока может быть скалярным, векторным или матричным сигналом.
Примеры использования блока Complex to Real-Imag показаны на рис. 9.6.13.
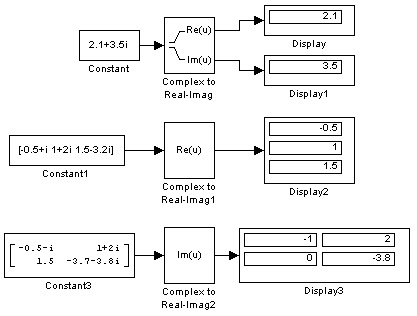
Рис. 9.6.13. Примеры использования блока Complex to Real-Imag
9.6.11. Блок вычисления модуля и (или) аргумена комплексного числа Complex to Magnitude-Angle
Назначение:
Вычисляет модуль и (или) аргумент комплексного числа.
Параметры:
Output – Выходной сигнал (выбирается из списка):
Magnitude – Модуль.
Angle – Аргумент.
MagnitudeAndAngle – Модуль и аргумент.
Входной сигнал блока может быть скалярным, векторным или матричным сигналом.
Примеры использования блока Complex to Magnitude-Angle показаны на рис. 9.6.14.
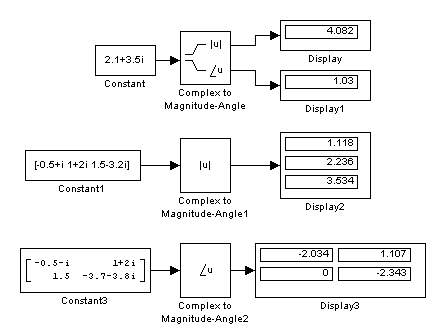
Рис. 9.6.14. Примеры использования блока Complex to Magnitude-Angle
9.6.12. Блок вычисления комплексного числа по его действительной и мнимой части Real-Imag to Complex
Назначение:
Вычисляет комплексное число по его действительной и мнимой части.
Параметры:
Input – Входной сигнал (выбирается из списка):
Real – Действительная часть.
Image – Мнимая часть.
RealAndImage – Действительная и мнимая часть.
Image part – Мнимая часть. Параметр доступен, если параметр Input объявлен как Real.
Real part – Действительная часть. Параметр доступен, если параметр Input объявлен как Image.
Входные сигналы блока могут быть скалярными, векторными или матричными. Параметры Image part и Real part должны задаваться как векторы или матрицы, если входной сигнал является вектором или матрицей.
Примеры использования блока Real-Imag to Complex показаны на рис. 9.6.15.

Рис. 9.6.15. Примеры использования блока Real-Imag to Complex
9.6.13. Блок вычисления комплексного числа по его модулю и аргументу Magnitude-Angle to Complex
Назначение:
Вычисляет комплексное число по его модулю и аргументу.
Параметры:
Input – Входной сигнал (выбирается из списка):
- Magnitude – Модуль.
- Angle – Аргумент.
- MagnitudeAndAngle – Модуль и аргумент.
Angle – Аргумент. Параметр доступен, если параметр Input объявлен как Magnitude.
Magnitude – Модуль. Параметр доступен, если параметр Input объявлен как Angle.
Входные сигналы блока могут быть скалярными, векторными или матричными.
Параметры Angle и Magnitude должны задаваться как векторы или матрицы, если входной сигнал является вектором или матрицей.
Примеры использования блока Magnitude-Angle to Complex показаны на рис. 9.6.16.

Рис. 9.6.16. Примеры использования блока Magnitude-Angle to Complex
9.6.14. Блок определения минимального или максимального значения MinMax
Назначение:
Определяет максимальное или минимальное значение из всех сигналов, поступающих на его входы.
Параметры:
Function - Выходной параметр. Выбирается из списка:
- min – Минимальное значение.
- max – Максимальное значение.
Number of input ports – Количество входных портов.
Входные сигналы блока могут быть скалярными или векторными. Блок определяет максимальное или минимальное значение из всех скалярных сигналов, поступающих на его входы. Если входные сигналы являются векторными, то блок выполняет поэлементную операцию поиска минимального или максимального значения. В этом случае размерности векторов должны совпадать. Если количество входных портов блока задано равным 1, то блок может использоваться для нахождения минимального или максимального значения во входном векторе.
Примеры использования блока MinMax показаны на рис. 9.6.17.
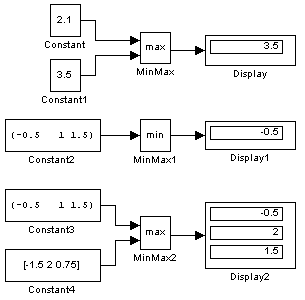
Рис. 9.6.17. Примеры использования блока MinMax
9.6.15. Блок округления числового значения Rounding Function
Назначение:
Выполняет операцию округления числового значения.
Параметры:
Function – Способ округления (выбирается из списка):
floor – Округление до ближайшего меньшего целого.
ceil – Округление до ближайшего большего целого.
round – Округление до ближайшего целого.
fix – Округление отбрасыванием дробной части.
Входные сигналы блока могут быть скалярными, векторными или матричными действительного и комплексного типа. При векторном или матричном входном сигнале блок выполняет поэлементные операции.
Выходной сигнал блока будет иметь тип double или single.
Примеры использования блока Rounding Function показаны на рис. 9.6.18.
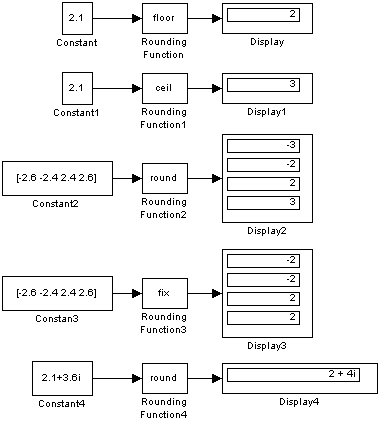
Рис. 9.6.18. Примеры использования блока Rounding Function
9.6.16. Блок вычисления операции отношения Relational Operator
Назначение:
Блок сравнивает текущие значения входных сигналов.
Параметры:
Relational Operator – Тип операции отношения (выбирается из списка):
= = - Тождественно равно.
~ = - Не равно.
< - Меньше.
< = - Меньше или равно.
> = - Больше или равно.
> - Больше.
В операции отношения первым операндом является сигнал, подаваемый на первый (верхний) вход блока, а вторым операндом – сигнал, подаваемый на второй (нижний) вход. Выходным сигналом блока является 1, если результат вычисления операции отношения есть “ИСТИНА” и 0, если результат – “ЛОЖЬ”.
Входные сигналы блока могут быть скалярными, векторными или матричными. Если оба входных сигнала – векторы или матрицы, то блок выполняет поэлементную операцию сравнения, при этом размерность входных сигналов должна совпадать. Если один из входных сигналов – вектор или матрица, а другой входной сигнал – скаляр, то блок выполняет сравнение скалярного входного сигнала с каждым элементом массива. Размерность выходного сигнала, в этом случае, будет определяться размерностью векторного или матричного сигнала, подаваемого на один из входов.
Для операций = = (тождественно равно) и ~ = (не равно) допускается использовать комплексные входные сигналы.
Входные сигналы также могут быть логического типа (boolean).
Примеры использования блока Relational Operator показаны на рис. 9.6.19.
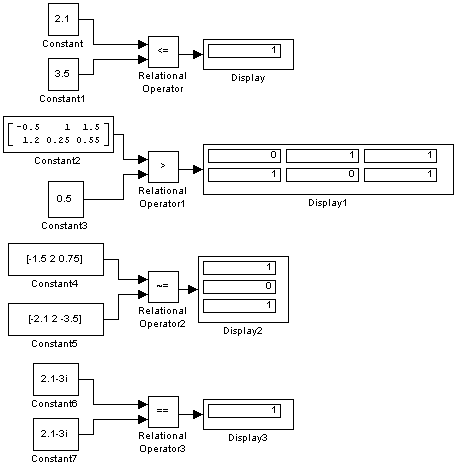
Рис. 9.6.19. Примеры использования блока Relational Operator
9.6.17. Блок логических операций Logical Operation
Назначение:
Реализует одну из базовых логических операций.
Параметры:
Operator – Вид реализуемой логической операции (выбирается из списка):
AND – Логическое умножение (операция И).
OR – Логическое сложение (операция ИЛИ).
NAND – Операция И-НЕ.
NOR – Операция ИЛИ-НЕ.
XOR – Исключающее ИЛИ (операция сложения по модулю 2).
NOT – Логическое отрицание (НЕ).
Number of input ports – Количество входных портов.
Выходным сигналом блока является 1, если результат вычисления логической операции есть “ИСТИНА” и 0, если результат – “ЛОЖЬ”.
Входные сигналы блока могут быть скалярными, векторными или матричными. Если входные сигналы – векторы или матрицы, то блок выполняет поэлементную логическую операцию, при этом размерность входных сигналов должна совпадать. Если часть входных сигналов – векторы или матрицы, а другая часть входных сигналов – скаляры, то блок выполняет логическую операцию для скалярных входных сигналов и каждого элемента векторных или матричных сигналов. Размерность выходного сигнала, в этом случае, будет определяться размерностью векторных или матричных входных сигналов.
При выполнении логической операции отрицания блок будет иметь лишь один входной порт.
Входные сигналы могут быть как действительного, так и логического типа (boolean).
Примеры использования блока Logical Operation показаны на рис. 9.6.20.
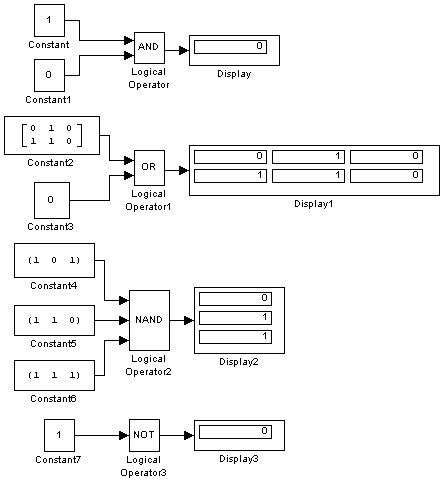
Рис. 9.6.20. Примеры использования блока Logical Operation
9.6.18. Блок побитовых логических операций Birwise Logical Operator
Назначение:
Реализует одну из базовых логических операций по отношению к целому числу в двоичном представлении.
Параметры:
Bitwise operator – Вид реализуемой логической операции (выбирается из списка):
AND – Логическое умножение (операция И).
OR – Логическое сложение (операция ИЛИ).
XOR – Исключающее ИЛИ (операция сложения по модулю 2).
NOT – Логическое отрицание (НЕ).
SHIFT_LEFT – Поразрядный сдвиг влево.
SHIFT_RIGHT – Поразрядный сдвиг вправо.
Second operand – Второй операнд. Задается шестнадцатеричным числом в символьном виде.
Одним из операндов блока Birwise Logical Operator является сигнал, подаваемый на вход блока, а вторым – параметр блока Second operand.
Входными сигналами блока должны быть беззнаковые переменные типа uint8, uint16 или uint32.
Входной сигнал блока может быть скалярным, векторным или матричным. Если входной сигнал – вектор или матрица и второй операнд также вектор или матрица, то блок выполняет поэлементную логическую операцию, при этом размерность операндов должна совпадать. Если один из операндов – вектор или матрица, а другой операнд – скаляр, то блок выполняет логическую операцию для скалярного операнда и каждого элемента векторного или матричного операнда. Размерность выходного сигнала, в этом случае, будет определяться размерностью векторного или матричного операнда.
При выполнении логической операции отрицания блок будет иметь лишь один операнд (входной сигнал).
Примеры использования блока Birwise Logical Operator показаны на рис. 9.6.21.

Рис. 9.6.21. Примеры использования блока Birwise Logical Operator
9.6.19. Блок комбинаторной логики Gombinatorical Logic
Назначение:
Преобразует входные сигналы в соответствии с таблицей истинности.
Параметры:
Truth table – Таблица истинности.
Блок Combinatorical Logic обеспечивает преобразование входного сигнала в соответствии с правилами, определяемыми таблицей истинности. Таблица истинности представляет собой список возможных выходных значений блока. Такое описание работы устройств принято в теории конечных автоматов. Число строк в таблице истинности определяется соотношением:
![]() ,
,
где
number of inрuts – число входных сигналов,
number of rows – число строк таблицы истинности.
Входные сигналы при составлении таблицы истинности считаются заданными. Они определяют индекс (номер) строки, в которой записываются выходные значения блока. Индекс каждой строки определяется выражением:
![]() ,
,
где
row index – индекс строки,
m – количество входных сигналов (элементов во входном векторе),
u(1) – первый входной сигнал (первый элемент входного вектора),
u(m) – последний входной сигнал (последний элемент входного вектора).
Например, в случае операции логического И (AND) для двух операндов выражение, определяющее индекс строки будет выглядеть следующим образом:
![]() .
.
Ниже приведен пример формирования таблицы истинности операции логического И (AND) для двух операндов:
Таблица 9.6.2
|
Вход 2 |
Вход 1 |
Выражение для |
Значение |
Таблица истинности |
|
0 |
0 |
|
1 |
0 |
|
1 |
0 |
|
2 |
0 |
|
0 |
1 |
|
3 |
0 |
|
1 |
1 |
|
4 |
1 |
На рис. 9.6.22 показан пример реализации операции логического И с помощью блока Combinatorical Logic. Параметр блока Truth table задан выражением [0;0;0;1].
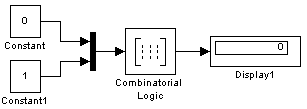
Рис. 9.6.22. Пример использования блока Combinatorical Logic
9.6.20. Блок алгебраического контура Algebraic Constraint
Назначение:
Выполняет поиск корней алгебраических уравнений.
Параметры:
Initial guess – Начальное значение выходного сигнала.
Блок находит такое значение выходного сигнала, при котором значение входного сигнала становится равным нулю. При этом входной сигнал должен быть прямо или опосредованно связан с входным сигналом.
На рис. 9.6.23 показан пример решения системы нелинейных уравнений вида:
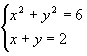 .
.
Поскольку данная система уравнений имеет два решения, то начальные значения блоков Algebraic Constraint заданы в виде векторов. Для первого (верхнего) блока начальное значение задано вектором [1 -1], а для второго (нижнего) блока – вектором [-1 1].
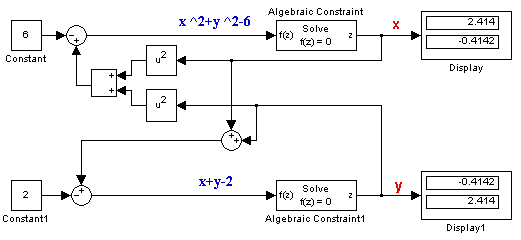
Рис. 9.6.23. Пример использования блока Algebraic Constraint
Блок Algebraic Constraint может использоваться также и для решения нелинейных матричных уравнений. На рис. 9.6.24 показан пример решения нелинейного матричного уравнения вида:
 .
.
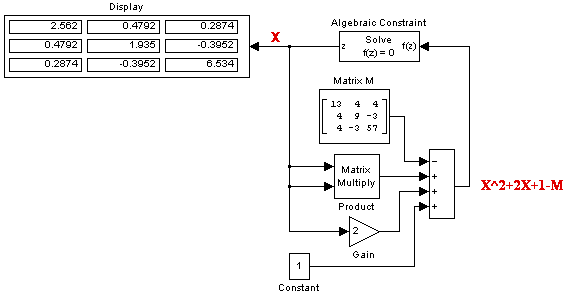
Рис. 9.6.23. Пример использования блока Algebraic Constraint для решения нелинейного матричного уравнения.
|
|