НЕКООПЕРИРОВАННАЯ ЦЕНОВАЯ ОЛИГОПОЛИЯ. МОДЕЛЬ ЭДЖУОРТА

Согласившись с критикой модели Курно Бертраном, Ф. Эджуорт предложил модель ценовой дуополии с ограничением на величину производственной мощности дуополистов.¹¹ На рис. 11.9 это ограничение представлено абсциссой вертикально восходящего сегмента кривой МС (затраты на производство дополнительной - сверх ограниченного масштаба мощности - единицы продукции бесконечно велики) q^k. Как видно из рис. 11.9, мощности каждого дуопо-листа ограничены половиной рыночного спроса при цене, равной предельным затратам, q^k = Q(P º MC)/2 . Поэтому, если каждый из них установит начальную цену равной предельным затратам (P₁ = P₂ = МС), их совместный выпуск как раз и покроет совокупный рыночный спрос, Q(P = МС).

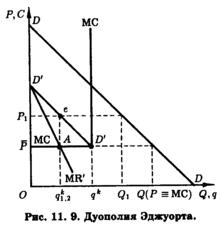
Если теперь дуополист 1 несколько повысит свою цену, тогда как дуополист 2 сохранит цену P₂ = МС, все покупатели захотят перейти к нему вследствие более низкой цены. Однако - и в этом отличие модели Эджуорта от модели Бертрана - он Не сможет покрыть более половины рыночного спроса, поскольку именно такова его производственная мощность. Разочарованные неспособностью дуополиста 2 удовлетворить их спрос по относительно более низким ценам покупатели вынуждены будут обратиться к дуополисту 1. Столкнувшись с остаточным спросом (Q(P º МС) - q^k), последний сможет максимизировать свою прибыль, действуя как монополист в отношении этого остаточного спроса. Его предельные затраты уравниваются с предельной выручкой в точке А, что предполагает установлением им прибылемаксимизирующей цены PJ , при которой выпуск составит q₁ - Q(P = MC)/4.

В ответ на это дуополист 2 повысит свою цену до уровня чуть ниже P₁, цены дуополиста 1, с тем чтобы привлечь к себе его покупателей. Однако из-за ограниченности своей производственной мощности дуополист 2 сможет покрыть спрос лишь в объеме Q₁ - q₁ = 2/3Q₁ = Q₁(P = МС)/2. Продавая по чуть более низкой, чем у дуополиста 1, цене вдвое больше продукции, дуополист 2 получит, вероятно, и вдвое большую прибыль. Тогда дуополист 1 в свою очередь снизит цену до уровня чуть ниже, чем цена дуополиста 2. Словом, они попытаются опередить друг друга в снижении цен. Попытки заработать на снижении цены будут продолжаться, пока она не достигнет уровня

Дуополисты будут рассуждать примерно так. Если я снижу свою цену до Р, что чуть ниже цены соперника, я смогу продать максимально возможный для меня объем выпуска, q^k. С другой стороны, если я увеличу свою цену до P₁, я смогу продать лишь q₁ единиц продукции. При какой цене Р моя прибыль окажется точно такой же, как и при цене P₁? Ответ на этот вопрос можно получить, решив относительно Р уравнение

Но как только цена действительно упадет до Р, выгодным для любого дуополиста вновь становится повышение цены до P₁, и весь ценовой цикл повторится. Таким образом, модель Эджуорта не предрекает никакого статичного равновесия. Скорее это некая "ценовая ловушка", попав в которую дуополисты втягиваются в нескончаемую ценовую войну, в которой падения цен чередуются с их всплесками.

КОЛИЧЕСТВЕННАЯ ИЛИ ЦЕНОВАЯ ОЛИГОПОЛИЯ?

Интуитивно можно предположить, что модель ценовой конкуренции более реалистично представляет поведение олигополистов, чем модель количественной олигополии. Причиной тому может быть большая легкость манипулирования ценами, чем объемами выпуска. Для того чтобы варьировать объемы выпуска, могут понадобиться и дополнительные инвестиции в производственные мощности, и время. Варьировать ценами проще и "дешевле", хотя и здесь существуют известные ограничения (уже заключенные договора на поставку продукции и покупку сырья и материалов, расходы на переиздание каталогов и прейскурантов и т. п.). Так что на деле модели количественной и ценовой олигополии не противостоят, а скорее дополняют друг друга, образуя достаточно широкий (и не ограниченный, как мы увидим ниже, лишь ими) инструментарий для анализа олигопольных рынков.¹²

Более того, если соперники выпускают не строго однородный (совершенно взаимозаменяемый), а хотя бы слабо дифференцированный продукт, поставщик которого может быть легко идентифицирован покупателем (по фирменному знаку, товарной марке), то небольшое снижение цены одним олигополистом, скорее всего, не приведет к массовому перетоку к нему покупателей, ранее потреблявших продукты соперников. Некоторые из них, безусловно, сохранят верность ставшему относительно более дорогим продукту другого олигополиста (англ. brand loyalty) - привычной марке сигарет, кофе, чая и т. п. В таком случае и дуополист Бертрана сможет (как и дуополист Курно) сохранить свою цену на уровне, превышающем его предельные затраты. Так что в случае не однородной, а дифференцированной олигополии цены не столь резко различаются, как в случае однородной.

Наконец, взаимодействие реальных олигополистов не статично, оно может быть достаточно продолжительным. И совсем не предопределено, что это взаимодействие всегда будет проходить по одному и тому же сценарию. Д. Крепе и Дж. Шейнкман показали, использовав двухпериодную теоретико-игровую модель дуополии с ограничениями на мощности, что исход Курно может быть достигнут и в том случае, если в первом периоде дуополисты определяют выпуски (накапливают мощности), а во втором назначают цены.¹³ Обсуждение этой модели выходит за пределы нашего курса. Суть же ее состоит в том, что количественный выбор в первом периоде и ценовой во втором приводят к исходу Курно, как если бы в случае однократного взаимодействия дуополисты следовали бы сценарию модели Курно.

Все без исключения рассмотренные нами модели поведения олигополистов базируются, как мы помним, на предположительных вариациях, или, иначе, на определенных предположениях соперников-олигополистов о поведении друг друга.

Произвольный характер этих предположений всегда был предметом критики так называемых классических моделей дуополии или олигополии (Курно, Штакельберга, Бертрана, Эджуорта). Одним из наиболее последовательных и авторитетных критиков основанных на концепции предположительных вариаций моделей олигополии был Дж. Стиглер.

В опубликованной в 1964 г. и ставшей знаменитой статье¹⁴ он прямо провозгласил: "Приемлемая теория олигополии не может начинаться с предположений о том, как представляет каждая фирма свою зависимость от других фирм".¹⁵ Суть поведения дуополистов, по мнению Стиглера, сводится к стремлению их к сговору с целью максимизации всей совокупной прибыли группы олигополистов, а "общая прибыль всей группы фирм в отрасли максимизируется, когда они действуют совместно, как один монополист".¹⁶ Следующий раздел и будет посвящен моделям сговора, или, как иногда говорят, кооперированной олигополии.

ПРИМЕЧАНИЯ

¹¹ Edgeivorth F. Papers Relating to Political Economy. London, 1925. Vol. 1. P. 111-142. См. также: Nichol A. Edgeworth's Theory of Duopoly Price // Econ. Journ, 1935. Vol. 45. March. P. 51-66; Schubic M., Levitan R. Market Structure and Behaviour. P. 64-65. Обсуждение модели Эджуорта см.: Чемберлин Э. Теория монополистической конкуренции. С. 70 - 81.

Фрэнсис Исядоро Эджуорт (1845-1926) - британский экономист и статистик, профессор политической экономии в Королевском колледже (1881-1891) и Оксфордском университете (1891-1922), президент Королевского статистического общества (1912-1914), член Британской академии наук (с 1903 г.). Одним из первых ввел в экономическую теорию кривые безразличия. С его именем также связаны такие понятия экономической теории, как "коробка Эджуорта" и "контрактная кривая" (см. главу 16).

¹² Интересный сравнительный обзор классических моделей дуополии Кур-но, Штакельберга и Бертрана представлен в книге: Kreps D. A Course in Micro-economic Theory. New York et al., 1990. P. 443-449.

¹³ Кreps D., Schetnkman J. Quantity Precommitment and Berrand Competition Yield Cournot Outcomes // Bell Jour. Econ. 1983, Vol. 14. P. 326-337.

¹⁴ Стиглер Дж. Теория олигополии // Теория фирмы. СПб., 1995. (Вехя экономической мысли ; Вып. 2).

¹⁵ Там же. С. 371.

¹⁶ Там же. С. 372. º

оглавление ДМ экономическая информатика визуальные среды - 4GL Теория и практика обработки информации

Знаете ли Вы, что целевая функция - это математическое выражение, отражающее выбранный критерий эффективности функционирования исследуемой системы в её математической модели.

НОВОСТИ ФОРУМА

Рыцари теории эфира