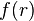 преобразование Абеля даётся уравнением:
преобразование Абеля даётся уравнением:Интегральное преобразование Абеля — преобразование, часто используемое при анализе
сферически или цилиндрически симметричных функций. Названо в
честь норвежского математика Нильса Хенрика Абеля.
Для функции 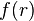 преобразование Абеля даётся уравнением:
преобразование Абеля даётся уравнением:
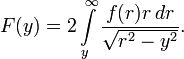
Если функция 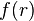 спадает с
спадает с
 быстрее чем
быстрее чем 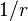 , то можно вычислить обратное
преобразование Абеля:
, то можно вычислить обратное
преобразование Абеля:
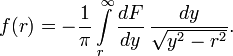
В обработке изображений преобразование Абеля используется для того, чтобы получить проекцию симметричной, оптически тонкой функции испускания на плоскость. Обратное преобразование используется для восстановления функции по её проекции (напр. фотографии).
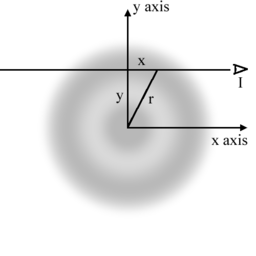
Геометрическая интерпретация
преобразования Абеля в двумерном случае. Наблюдатель (I) смотрит вдоль линии,
параллельной оси  на расстоянии
на расстоянии  от центра. Наблюдатель видит проекцию (интеграл)
осе-симметричной функции
от центра. Наблюдатель видит проекцию (интеграл)
осе-симметричной функции 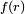 вдоль направления наблюдения. Функция
вдоль направления наблюдения. Функция 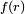 изображена при
помощи серого цвета. Предполагается, что наблюдатель находится так далеко от
центра, что пределы интегрирования равны
изображена при
помощи серого цвета. Предполагается, что наблюдатель находится так далеко от
центра, что пределы интегрирования равны 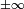 .
.
Преобразование Абеля в двумерном случае 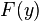 может рассматриваться как проекция
осесимметричной функции
может рассматриваться как проекция
осесимметричной функции 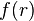 вдоль параллельных линий, проходящих на расстоянии
вдоль параллельных линий, проходящих на расстоянии 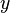 от оси. Согласно рисунку справа, наблюдатель (I)
увидит величину
от оси. Согласно рисунку справа, наблюдатель (I)
увидит величину
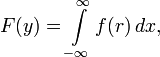
где 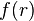 —
осесимметричная функция, изображенная на рисунке при помощи серого цвета.
Предполагается, что наблюдатель находится при
—
осесимметричная функция, изображенная на рисунке при помощи серого цвета.
Предполагается, что наблюдатель находится при 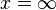 и таким образом пределы интегрирования равны
и таким образом пределы интегрирования равны 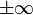 . Все линии наблюдения
параллельны оси
. Все линии наблюдения
параллельны оси 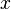 .
.
Замечая, что радиус  соотносится с
соотносится с 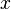 и
и 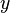 как
как 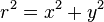 , получаем, что
, получаем, что
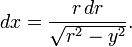
Так как переменная  при интегрировании не меняет знака,
то подынтегральное выражение (как
при интегрировании не меняет знака,
то подынтегральное выражение (как 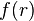 , так и выражение для
, так и выражение для 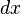 ) является чётной функцией. Поэтому можно записать:
) является чётной функцией. Поэтому можно записать:
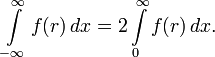
Замена переменной 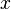 на
на  даёт формулу преобразования
Абеля:
даёт формулу преобразования
Абеля:
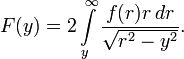
Преобразование Абеля можно обобщить на случай большего числа измерений.
Особенно интересен случай трёх измерений. В случае осесимметричной функции 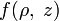 , где
, где 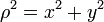 является радиусом в цилиндрических
координатах, можно спроектировать функцию на плоскость,
параллельную оси
является радиусом в цилиндрических
координатах, можно спроектировать функцию на плоскость,
параллельную оси 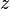 . Без потери
общности можно взять плоскость, параллельную плоскости
. Без потери
общности можно взять плоскость, параллельную плоскости 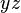 . При этом:
. При этом:
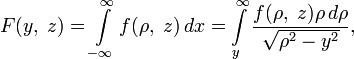
что является преобразованием Абеля для 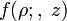 в переменных
в переменных 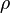 и
и 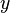 .
.
Частным случаем осевой симметрии является сферическая симметрия. В этом
случае имеется функция 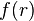 ,
где
,
где 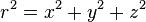 .
.
Проекция на плоскость 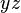 будет иметь круговую симметрию, которую можно записать как
будет иметь круговую симметрию, которую можно записать как  , где
, где 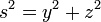 . Производя интегрирование, получим:
. Производя интегрирование, получим:
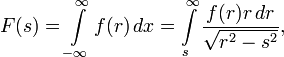
что опять является преобразованием Абеля для 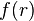 в переменных
в переменных  и
и  .
.
Преобразование Абеля является членом так называемого цикла Фурье —
Хенкеля — Абеля. Например для случая двух измерений, если обозначить через
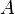 преобразование Абеля,
преобразование Абеля, 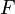 — преобразование
Фурье и через
— преобразование
Фурье и через 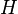 — преобразование
Хенкеля нулевого порядка, то для функций с круговой симметрией будет выполняться равенство:
— преобразование
Хенкеля нулевого порядка, то для функций с круговой симметрией будет выполняться равенство:
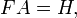
то есть если применить к одномерной функции сначала преобразование Абеля, а затем преобразование Фурье, то результат будет тот же, как после применения к функции преобразования Хенкеля.
|
|