УМОВ Николай Алексеевич
ЗАКОНЫ КОЛЕБАНИИ В НЕОГРАНИЧЕННОЙ СРЕДЕ ПОСТОЯННОЙ УПРУГОСТИ
Впервые напечатано в Математическом сборнике, т. 5, 1870 г. (Прим. ред.)
II. ЗАКОНЫ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ
§ 11. Подставляя величины Л', В', Г' из уравнений (14) в уравнения (15), мы находим после приведений и сокращений;
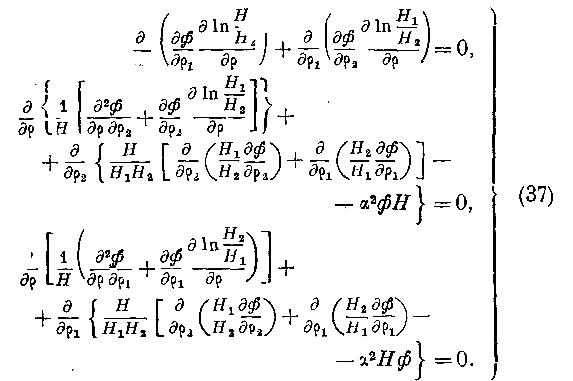
Если интеграл этих уравнении будет представлен рядом
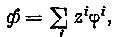
где
z' есть функция индекса i от {, и ср! есть функция индекса i от [ч, ;•;,, причём каждый член ряда отдельно удовлетворяет уравнениям (37), то первое из них распадается на три уравнения, вообще говоря, не тождественных.Действительно, замечая, что
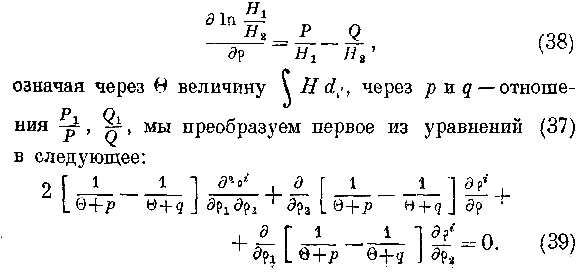
Производя указанные дифференцирования, размещая члены по нисходящим степеням в и замечая, что коэффициенты при них не зависят от
\>, заключаем, что каждый из них отдельно обращается в нуль, откуда и получаем следующие выражения: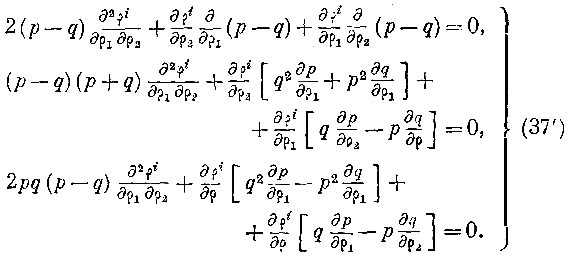
Частный случай. Исследуем з
;словия, при которых предыдущие выражения обращаются в тождество.Означая через
oF частную производную от F по одной из переменных р]; р3, мы находим из предыдущих уравнений: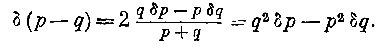
Это тройное равенство заключает два различных:
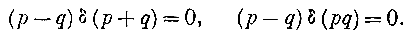
Эти последние возможны при двух условиях для
p и д: или р~д, или p = c.onst., q=consi. (40)Как то, так и другое приводят нас к сфере, если ни одно из уравнений (14) не обращается в тождество. Но поп последнем из условий (40) можно избежать равенства р— д, а следовательно, случая сферы, только когда оба уравнения (14) обращаются тождественно в нуль, и тогда уравнения (15) показывают, что поверхность волны будет в этом случае круглым цилиндром.
Объинтегрируем уравнения (37) для сферы. Первое из них тождественно обращается в нуль, и так как
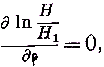
то последние два уравнения по интеграции дают,полагая
H—i, заменяя Нг, Н2 их величинами и я через а ]/' — 1: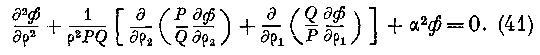
Означая через
p число целое, мы удовлетворим этому выражению, полагая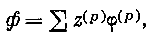
где суммирование производится по индексу
p и <р(р)> z(p~> суть функции — первая одного р, вторая одних ^ [i2, удовлетворяющие дифференциальным уравнениям1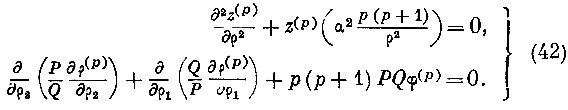
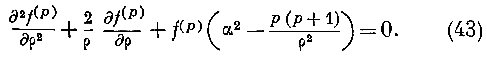
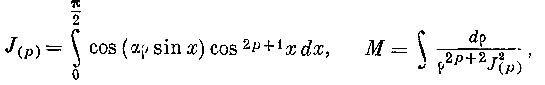
Полагая в первом из этих уравнений z^p)—p • f-p\ где /С'') есть функция одного \>, мы преобразуем его б следующее:
имеем, означая через С и В две произвольные постоянные:
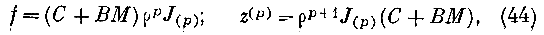
В § 4 было указано, что для сферы при известном выборе координат
P=l,
<? = cosPl.Подставляя эти выражения во второе из уравнений (42) и означая
sini.j через а, находим: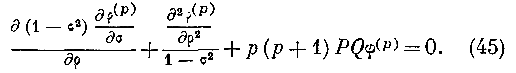
В случае полной сферы функция <р(р) должна оставаться конечной для всех значений переменных
\>^, (i2; она не должна изменяться, когда [>2 возрастает на одну или несколько окружностей; переменная р2 должнаисчезать при рх= ± ^ . Функция
^i>\ удовлетворяющая всем этим уело иям, известна и имеет вид: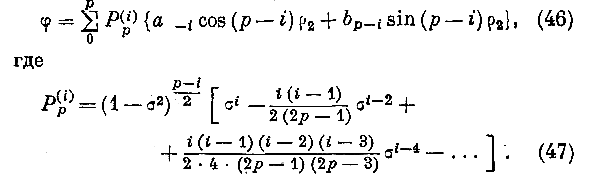
Злая <р('')
u 2^J), мы знаем функцию g5, из которой дифференцированием получаем амплитуды и и о.
|
|