УМОВ Николай Алексеевич
ЗАКОНЫ КОЛЕБАНИИ В НЕОГРАНИЧЕННОЙ СРЕДЕ ПОСТОЯННОЙ УПРУГОСТИ
Впервые напечатано в Математическом сборнике, т. 5, 1870 г. (Прим. ред.)
П. ЗАКОНЫ ПОПЕРЕЧНЫХ КОЛЕБАНИЙ
§ 7. Дифференциальные законы колебаний в средах постоянной упругости имеют в криволинейных координатах следующий вид:
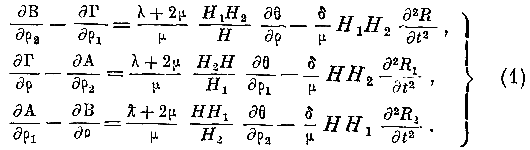
Здесь
R, ri, R.2 суть слагающие колебаний по нормалям к поверхностям р, [,г, ps. Величина 0 есть куби-ческое расширение,
X и р. — постоянные коэффициенты, о—плотность. Кроме того,
Мы начнем с приложения этих уравнении к колебаниям поперечным.
Так как поверхность
p есть поверхность волны, то для определения законов поперечных колебаний остаётся положить равным нулю продольное колебание R и кубическое расширение 0, чтобы из выражений (1) исчезли члены, зависящие от скорости распространения продольных колебаний.Означая скорость распространения поперечных колебаний через W, мы получаем из выражений (1), (2) и (3) следующие:

Эти уравнения с частными производными представляют зависимость между видом волны и поперечных колебаний, происходящих на её поверхности.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|