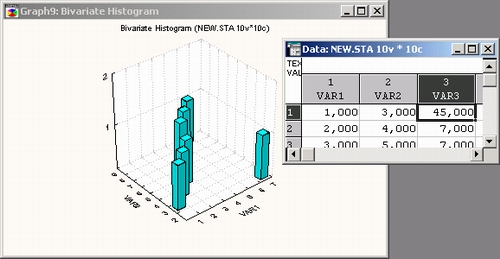
Трехмерный визуальный анализ позволяет анализировать данные в трехмерном пространстве, например, строить трехмерное изображение последовательностей исходных данных (наблюдений) для одной или нескольких выбранных переменных. Выбранные переменные представляются по оси Y, последовательные наблюдения — по оси X, а значения переменных (для данного наблюдения) откладываются по оси Z, как показано ниже:

Такие трехмерные графики используются для визуализации последовательностей значений нескольких переменных. По своей идее они сходны с составными линейными графиками, с тем лишь отличием, что для 3М диаграмм исходных данных ленты, линии, параллелепипеды и другие трехмерные представления значений каждой переменной не перекрываются (как на двухмерном графике), а «раздвигаются» в трехмерной перспективе.

ЗМ диаграммы исходных данных применяются как для отображения данных, так и для аналитических исследований. Наиболее типичным приложением ЗМ диаграмм исходных данных является наглядное представление имеющейся информации (например, о ценах, о росте населения, о взаимосвязи объемов продаж и прибыли). Такие графики позволяют просто и эффектно представить последовательности наблюдений, таких, например, как различные типы временных рядов.
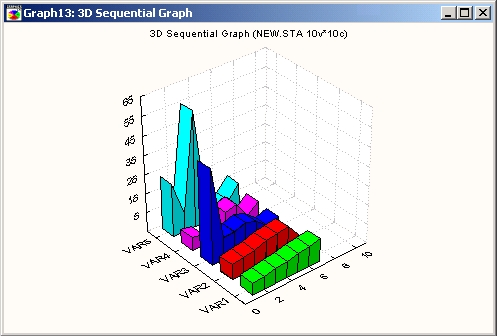
Основное преимущество трехмерных представлений перед двухмерными составными линейными графиками заключается в том, что для некоторых множеств данных при объемном изображении легче распознавать отдельные последовательности значений. При выборе подходящего угла зрения с помощью, например, интерактивного вращения линии графика не будут перекрываться или «попадать друг на друга», как часто бывает на составных линейных двухмерных графиках.
Трехмерные диаграммы также используются в аналитических целях при исследовании входных данных, имеющих матричный формат.
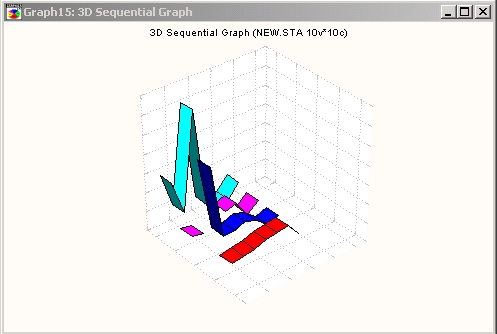
Для интерактивного просмотра поперечных сечений таких трехмерных представлений можно использовать метод динамического расслоения.
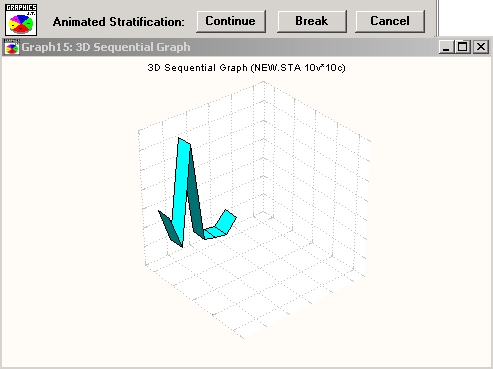
Заметьте, что для детального исследования изображения отдельные зависимости (то есть переменные) на графике можно выборочно выделить цветом. Для этого нужно нажать левую кнопку мыши в любом месте выбранной зависимости.
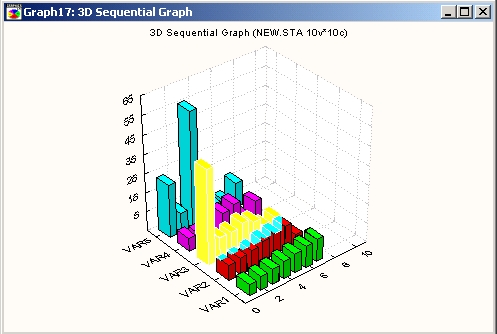
Процесс «просвечивания» дает возможность временно отобразить (с помощью подсветки) целые серии данных, даже если они почти полностью закрыты другими данными.
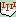 Столбчатая диаграмма
Столбчатая диаграмма
Этот последовательный график представляет отдельные значения одной или нескольких серий данных по оси Х в виде серий трехмерных столбцов (параллелепипедов). Все серии отделены друг от друга промежутками вдоль оси Y. Высота каждого столбца по оси Z отвечает значению соответствующей точки данных.
 Блоковая диаграмма
Блоковая диаграмма
Этот последовательный график представляет отдельные значения одной или нескольких серий данных по оси X в виде серий «трехмерных блоков». Все серии отделены друг от друга промежутками вдоль оси Y. Высота начала каждого блока по оси Z отвечает значению соответствующей точки данных.

 Ленточная диаграмма
Ленточная диаграмма
Эта диаграмма представляет отдельные значения одной или нескольких серий данных по оси X в виде серий «лент» в трехмерном пространстве.
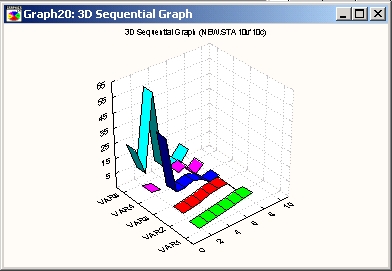
Все серии отделены друг от друга промежутками вдоль оси Y. Высота начала каждой ленты по оси Z отвечает значению соответствующей точки данных.
 Линейный график
Линейный график
Этот последовательный график представляет отдельные значения одной или нескольких серий данных по оси X в виде ряда непрерывных линий в трехмерном пространстве.
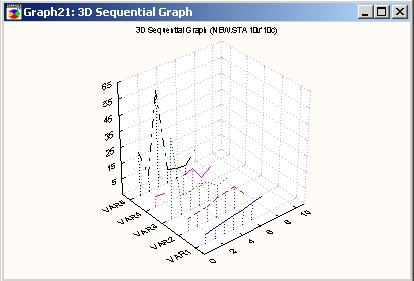
Все серии отделены друг от друга промежутками на оси Y. Высота начала каждой линии по оси Z отвечает значению соответствующей точки данных.
 Диаграмма всплесков
Диаграмма всплесков
Данный последовательный график представляет отдельные значения одного или нескольких наборов данных по оси Х в виде серий «всплесков» (точек с перпендикулярами, опущенными на плоскость основания).
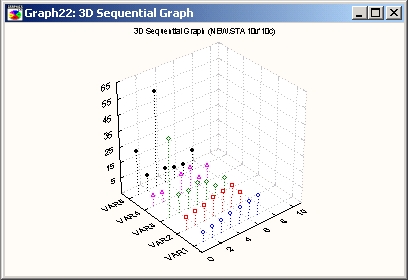
Все серии отделены друг от друга промежутками вдоль оси Y. Высота каждого перпендикуляра по оси Z отвечает соответствующему значению серии.
 Дискретная карта линий уровня
Дискретная карта линий уровня
Этот последовательный график можно рассматривать как двухмерную проекцию ЗМ ленточной диаграммы.
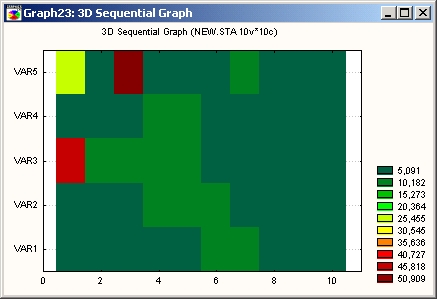
На этом графике каждая точка данных представлена в виде прямоугольной области; значениям (или диапазону значений) точек данных соответствуют различные цвета или шаблоны (цветовые шаблоны описаны справа от графика). Значения из одной серии представлены по оси X, а сами серии откладываются по оси Y.
 График поверхности
График поверхности
На последовательном графике к точкам исходных данных подгоняется сглаженная сплайнами поверхность.
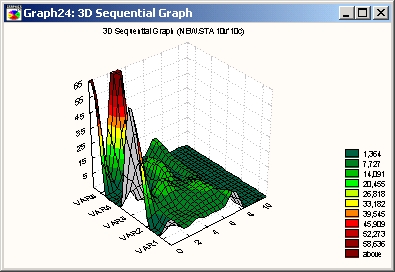
Последовательные значения каждой серии откладываются по оси X, а сами последовательные серии представлены на оси Y.
 Карта линий уровня
Карта линий уровня
Карта линий уровня представляет собой двухмерную проекцию сглаженной сплайнами поверхности, подогнанной к исходным данным.
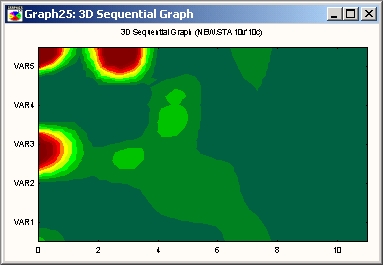
Последовательные значения каждой серии откладываются по оси X, а сами последовательные серии представлены на оси Y.
Трехмерные, или ЗМ, гистограммы двух переменных используются для визуализации табулированных значений двух переменных или для визуализации таблиц сопряженности двух переменных. Их можно рассматривать как сочетание двух простых гистограмм (то есть гистограмм одной переменной), соединенных таким образом, чтобы можно было исследовать частоты совместного появления значений двух переменных.

Распределение частот на трехмерных гистограммах вызывает интерес по двум причинам:
ЗМ гистограммы и кросстабуляции
ЗМ гистограммы двух переменных предоставляют ту же информацию, что и таблицы сопряженности. Хотя некоторые (числовые) данные по частотам легче воспринимать в виде таблицы, общая форма и глобальные описательные характеристики распределения двух переменных легче исследовать на графике.
Более того, график дает качественную информацию о распределении, которую нельзя полностью выразить каким-то одним показателем. Например, асимметричное распределение двух переменных — скрытых откликов и времени реакции (в эксперименте измерения времени реакции) — может проистекать из изменений поведения субъектов при усталости.
Категоризация значений
Все процедуры построения гистограмм имеют стандартный набор методов категоризации, или разбиения наблюдений на группы. Систематично методы категоризации изложены в отдельной главе.
Согласно этим методам, диапазон значений каждой из двух выбранных для графика переменных разбивается на категории (классы), для которых подсчитываются частоты, отображаемые в виде отдельных трехмерных столбцов.
Например, можно построить трехмерную гистограмму, на которой каждый столбец будет соответствовать 10 единицам шкалы, используемой для переменной; если минимальное значение равно 0, а максимальное равно 120, то будет построено 12 рядов столбцов. В качестве другого примера можно разделить диапазон значений переменных на определенное число равных интервалов (например, 10); в последнем случае если минимум равен 0, а максимум равен 120, то каждый интервал будет равен 12 единицам шкалы. Существует возможность проводить и более сложную категоризацию.
Так можно создать неравные интервалы группировки, задавая их границы (например, для создания легко интерпретируемой картинки или для связывания выбросов и улучшения представления средней части гистограммы, в которой сосредоточена большая часть наблюдений). Диапазоны также могут быть созданы с помощью логических выражений (например, первый столбец гистограммы может представлять людей, которые в прошлом году путешествовали самолетом более 10 раз, и тех, кто проводит более 20% времени в деловых поездках и т. п.).
Различные способы категоризации на одном графике
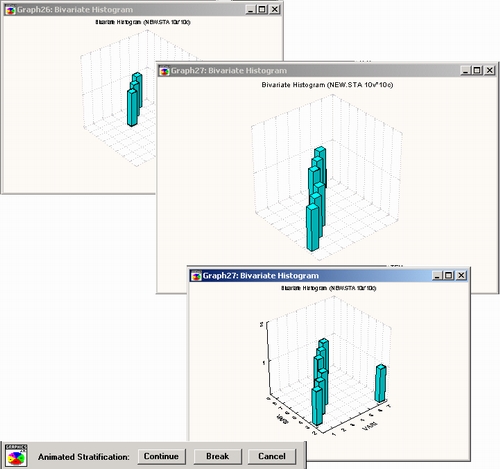
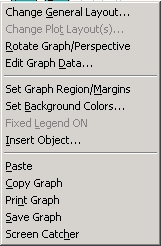
Для каждой из двух переменных, распределение которых представлено на графике, могут быть использованы различные методы категоризации, как показано на следующей ЗМ гистограмме двух переменных значений температуры и степени комфорта.
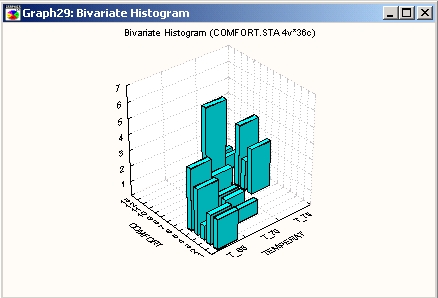
В частности, на этом графике распределение времен реакции (непрерывной переменной, категоризованной путем разделения всего диапазона значений на 12 интервалов равной длины) представлено для трех условий эксперимента (дискретной переменной с тремя уровнями, имеющими разные метки: Основной — BASE, Нормальный — NORMAL и Двойной — DOUBLE).
Запомните, все элементы графика можно изменить, щелкнув, например, на нем правой кнопкой мыши и вызвав контекстное меню графиков.
Сглаживание распределений двух переменных
Процедуры сглаживания для ЗМ гистограмм двух переменных позволяют подгонять поверхности к трехмерным изображениям данных частот двух переменных. Так, например, каждая трехмерная гистограмма может быть превращена в сглаженную поверхность. Это представление нецелесообразно использовать для простых категоризованных данных (таких, как изображенная выше гистограмма).
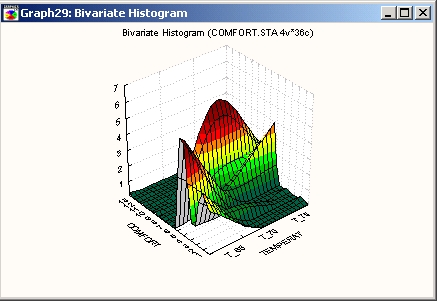
Однако этот способ может оказаться ценным средством для исследования сложной структуры частот.

Он позволяет обнаруживать закономерности, менее заметные на стандартной трехмерной гистограмме, например, «волнистую» поверхность на показанном выше рисунке.
Подобно статистическим 2М диаграммам диапазонов трехмерные диаграммы диапазонов отображают диапазоны значений или столбцы ошибок, соответствующих определенным точкам данных.
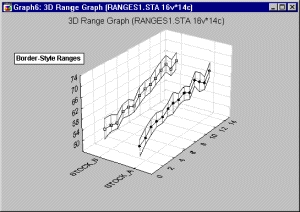
Диапазоны или столбцы ошибок не вычисляются по данным, а определяются исходными значениями выбранных переменных. Для каждого наблюдения строится один диапазон или столбец ошибок. Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от средней точки. На графике можно представить одну или несколько переменных.
В основном диаграммы диапазонов используются для изображения: а) диапазонов значений для отдельных элементов анализа (наблюдений, выборок и т. д.) или б) вариации значений в отдельных группах или выборках (последнее имеет смысл, когда величины вариации получены при независимых измерениях; иначе более целесообразно использовать ЗМ диаграммы размаха, которые вычисляют вариацию для выборок, представленных на графике). Некоторые из этих приложений кратко описаны в разделе ЗМ диаграммы размаха.
Основное различие между диаграммами диапазонов и диаграммами размаха состоит в том, что на диаграммах диапазонов все значения, определяющие диапазоны («средние точки», минимум и максимум), не вычисляются по данным, а являются исходными значениями переменных.
Когда на графике нужно представить только одну переменную, обычно достаточно воспользоваться 2М диаграммой диапазонов; на этом графике также можно представить несколько переменных (путем сдвига изображений так, что для каждого наблюдения будет отображено последовательно столько диапазонов, сколько переменных используется для анализа). Тем не менее ЗМ диаграмма диапазонов часто является более подходящим способом представления диапазонов нескольких переменных на одном графике, т. к. она не «разбивает» строки пиктограмм, представляющих отдельные классы или переменные.
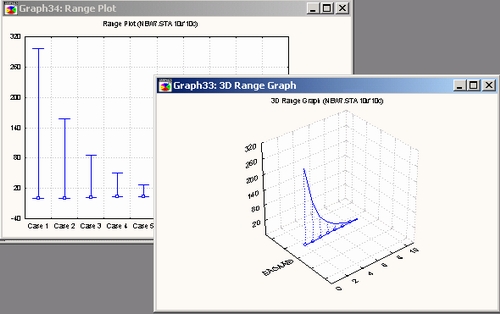
После создания графика можно изменить его расположение и вид отдельных элементов. Для этого нужно открыть диалоговое окно Общая разметка: ЗМ графики (с помощью двойного щелчка мышью на фоне графика или из графического выпадающего меню Разметки) или диалоговое окно Размещение ЗМ графика (с помощью команды контекстного меню, вызываемого правой кнопкой мыши для конкретной зависимости, или из графического выпадающего меню Разметки).
 Точечные диапазоны
Точечные диапазоны
На статистической ЗМ последовательной диаграмме диапазонов такого типа диапазоны изображены в виде маркеров точек (соединенных линией).
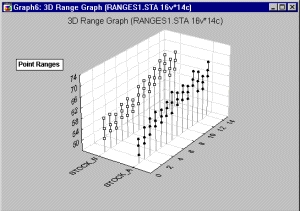
Для каждого наблюдения строится один диапазон. Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от средней точки в зависимости от текущего значения параметра Тип (значения диапазона).
 Граничные диапазоны
Граничные диапазоны
На статистической ЗМ последовательной диаграмме диапазонов такого типа диапазоны представлены двумя непрерывными линиями (верхние и нижние диапазоны). Средние точки изображены в виде маркеров точек, соединенных линией.
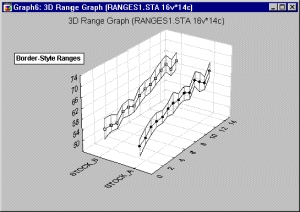
Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от центральной точки, в зависимости от текущего значения параметра Тип (значения диапазона).
 Диапазоны ошибок
Диапазоны ошибок
На статистической ЗМ последовательной диаграмме диапазонов такого типа средние точки изображены в виде маркеров точек, а диапазоны — в виде столбцов ошибок. Для каждого наблюдения строится один столбец ошибок.
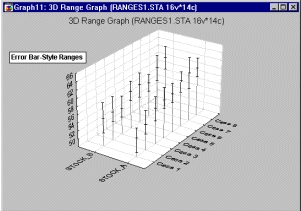
Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от центральной точки, в зависимости от текущего значения параметра Тип (значения диапазона).
 Диапазоны двойных лент
Диапазоны двойных лент
На статистической ЗМ последовательной диаграмме диапазонов такого типа диапазоны представлены двумя лентами (верхние и нижние диапазоны).

Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от средней точки в зависимости от текущего значения параметра Тип (значения диапазона). Средние точки на графике не изображаются (они могут быть показаны на одном из первых трех типов диаграмм диапазонов).
 «Летящие ящики»
«Летящие ящики»
На статистической ЗМ последовательной диаграмме диапазонов такого типа диапазоны представлены в виде «летящих ящиков». Ящики не закреплены на плоскости, а как бы парят в пространстве. В ряде случаев такие графики чрезвычайно эффектны для зрительного восприятия.
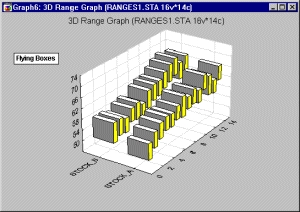
Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от средней точки, в зависимости от текущего значения параметра Тип (значения диапазона). Средние точки на графике не изображаются (они могут быть показаны на одном из первых трех типов диаграмм диапазонов).
 «Летящие блоки»
«Летящие блоки»
На статистической ЗМ последовательной диаграмме диапазонов такого типа диапазоны представлены «летящими блоками».
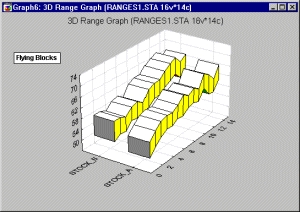
Переменные диапазона можно понимать как абсолютные значения или как значения, отвечающие отклонениям от средней точки, в зависимости от текущего значения параметра Тип (значения диапазона). Средние точки на графике не изображаются (они могут быть показаны на одном из первых трех типов диаграмм диапазонов).
Подобно статистическим 2М диаграммам размаха на ЗМ диаграммах размаха диапазоны значений выбранной переменной строятся отдельно для групп наблюдений, определяемых значениями категоризующей (группирующей) переменной. Центральная тенденция (например, медиана или среднее) и диапазон или вариационные статистики (например, квартили, стандартные ошибки или стандартные отклонения) вычисляются для каждой группы наблюдений, а стиль изображения определяется Типом графика.
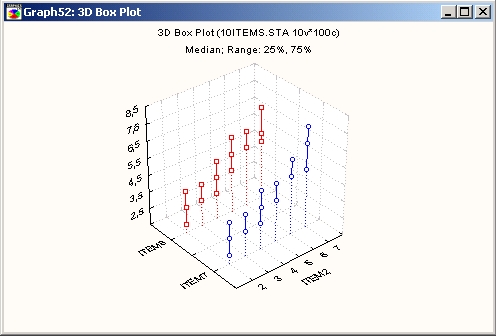
ЗМ диаграммы диапазонов отличаются от ЗМ диаграмм размаха тем, что на диаграммах диапазонов диапазоны представлены значениями выбранных переменных (например, одна переменная содержит минимальные значения диапазонов, а другая — максимальные значения диапазонов), а для диаграмм размаха диапазоны вычисляются по значениям переменных (например, стандартные отклонения, стандартные ошибки или минимальные и максимальные значения).
Как правило, диаграммы размаха используются в двух случаях: а) для изображения диапазонов значений для отдельных наблюдений или выборок (например, типичная минимаксная диаграмма для акций или товаров или агрегированные последовательные графики данных с диапазонами) или б) для изображения вариации значений в отдельных группах или выборках (например, диаграммы размаха, изображающие медиану или среднее для каждой выборки в виде точки внутри «летящего» столбца ошибок, а также стандартные ошибки или квартальный размах, представленные в виде «летящих ящиков»; см. рисунок ниже).
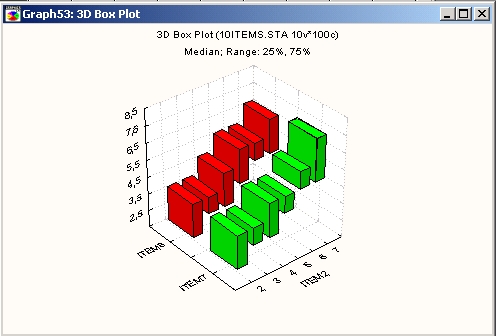
Диаграммы размаха, показывающие вариацию значений, легко позволяют оценить и «интуитивно представить» силу связи между группирующей переменной и одной или несколькими зависимыми переменными. В частности, предполагая, что зависимые переменные нормально распределены, и зная, какая часть наблюдений попадает, например, в интервал ±1 или ±2 стандартных отклонения от среднего, можно легко понять результаты эксперимента и сделать вывод, что, например, результаты примерно в 95% наблюдений в экспериментальной группе 1 принадлежат диапазону, отличному от диапазона значений порядка 95% наблюдений в группе 2.
Когда на графике нужно представить только одну переменную, обычно достаточно воспользоваться 2'Мдиаграммой размаха; на этом графике можно также представить несколько переменных (путем сдвига изображений отдельных «ящиков» так, что для каждого наблюдения будет изображено последовательно столько «ящиков», сколько переменных используется для анализа). Тем не менее для представления нескольких переменных на одном графике более подходящей является ЗМ диаграмма размаха, т. к. она не «разбивает» строки пиктограмм для каждой переменной. Например, это часто делает более ясной схему расположения средних и стандартных отклонений или квартальных размахов в выбранных категориях.
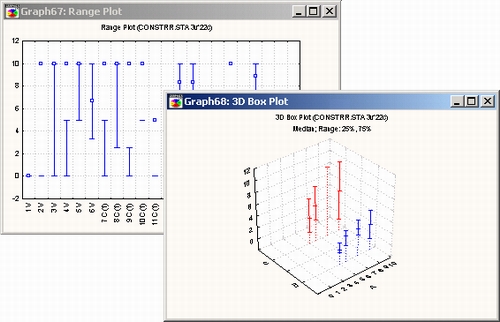
 Граничные диапазоны
Граничные диапазоны
На статистической ЗМ диаграмме размаха вычисленные по исходным данным диапазоны (например, квартили) представлены двумя непрерывными линиями (верхние и нижние диапазоны).
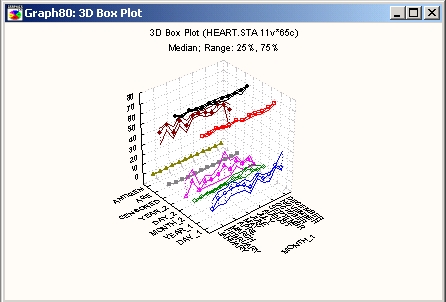
Средние точки (средние значения или медианы) отображаются маркерами точек и соединены линиями.
 Диапазоны ошибок
Диапазоны ошибок
На статистической ЗМ диаграмме размаха такого типа средние точки (вычисленные по данным средние значения или медианы) изображены маркерами точек, а вычисленные диапазоны (например, квартили) представлены столбцами ошибок.

Для каждого уровня независимой (группирующей) переменной рисуется один столбец ошибок.
 Точечные диапазоны
Точечные диапазоны
На статистической ЗМ диаграмме размаха такого типа средние точки и вычисленные диапазоны (например, квартили) представлены тройками маркеров точек (соединенных линией).
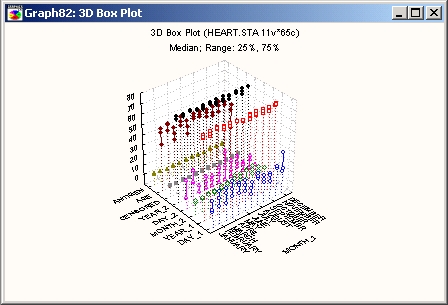
Для каждого уровня независимой (группирующей) переменной строится одна тройка значений.
 Диапазоны двойных лент
Диапазоны двойных лент
На статистической ЗМ диаграмме размаха такого типа вычисленные диапазоны (например, квартили) представлены двумя лентами (верхние и нижние диапазоны).

На диаграмме этого типа средние точки не изображаются. Чтобы их показать, необходимо перейти к одному из первых трех типов диаграмм размаха (см. выше).
 «Летящие ящики»
«Летящие ящики»
На статистической ЗМ диаграмме размаха этого типа вычисленные диапазоны (например, квартили) представлены в виде «летящих ящиков».
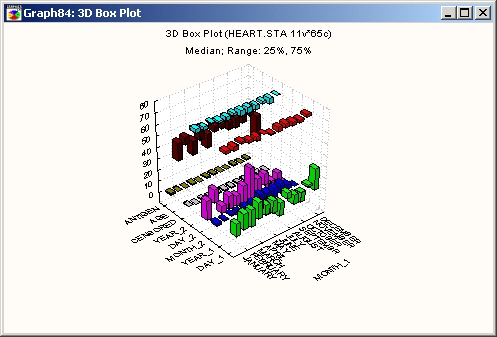
На диаграмме средние точки не изображаются. Чтобы их показать, необходимо перейти к одному из первых трех типов диаграмм размаха.
 «Летящие блоки»
«Летящие блоки»
На статистической ЗМ диаграмме размаха вычисленные диапазоны (например, квартили) представлены в виде «летящих блоков».

На диаграмме средние точки не изображаются. Чтобы их показать, необходимо перейти к одному из первых трех типов диаграмм размаха.
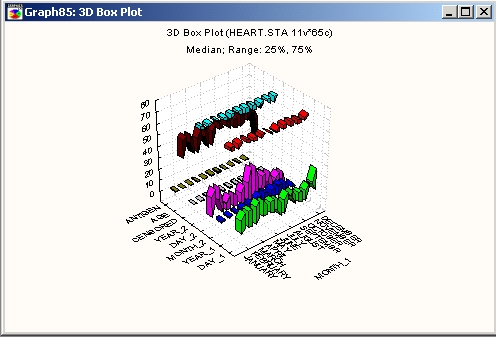
Если увеличить установленное по умолчанию значение поля X (0%), то между отдельными «летящими блоками» появятся разрывы, как показано выше на графике.
 Всплески
Всплески
При выборе этого режима точечные диапазоны или столбцы ошибок будут соединены с основанием графика линиями.

Трехмерные диаграммы рассеяния
Трехмерные диаграммы рассеяния (называемые также XYZ диаграммами рассеяния) представляют собой наиболее простой тип трехмерных зависимостей. Как правило, они используются для визуализации связей между непрерывными переменными.
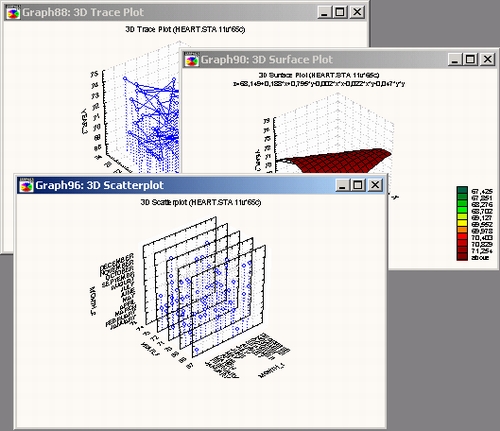
Хотя можно найти различные применения трехмерных диаграмм рассеяния, тем не менее их основное преимущество состоит в наглядном представлении сложных взаимосвязей между несколькими переменными.
Рассмотрим простой пример из области маркетинга. Предположим, за определенный период времени (в различное время суток) проводились исследования цены и предложения товара. Если построить на графике значения трех этих переменных (Price, Supply и Hour), то можно выявить сложные многомерные интерактивные связи, которые практически невозможно обнаружить при численном анализе данных.
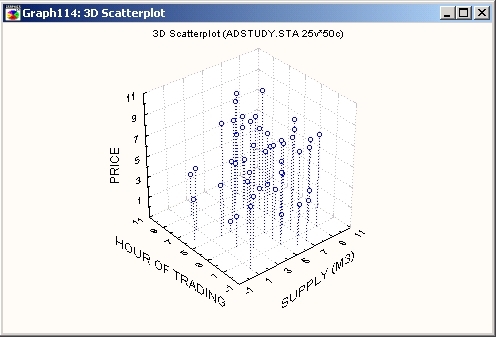
Например, можно установить, что взаимосвязь усиливается во второй половине дня (становится теснее связь между ценой и предложением товара). Однако по форме графика также видно, что эта связь не сохраняется при низком уровне предложения (то есть при малых значениях переменной Supply). Часто такие сложные взаимосвязи легче выявить на графике, чем при использовании численных методов, особенно в случае криволинейных зависимостей. Выделение кластеров и подмножеств на выборке из неоднородной совокупности Существует и другая область разведочного анализа данных, где могут быть полезны XYZ диаграммы рассеяния. Это те случаи, когда ожидается наличие групп наблюдений, которые могут быть выявлены только при исследовании распределения одновременно по трем переменным. Например, на следующей XYZ диаграмме рассеяния показаны «классические» данные по классификации ирисов (Fisher, 1936; файл Irisdat.sta), которые включают наблюдения различных видов ирисов.
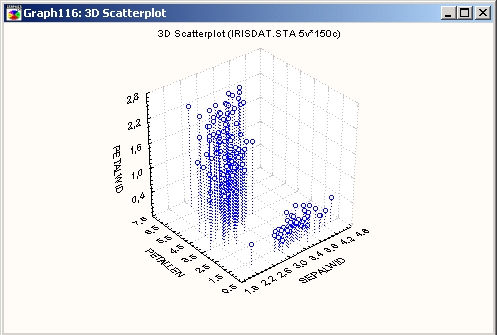
Из графика видно, что, построив зависимость ширины лепестков от их длины и ширины чашелистиков, можно сделать вывод о том, что выборка неоднородна.
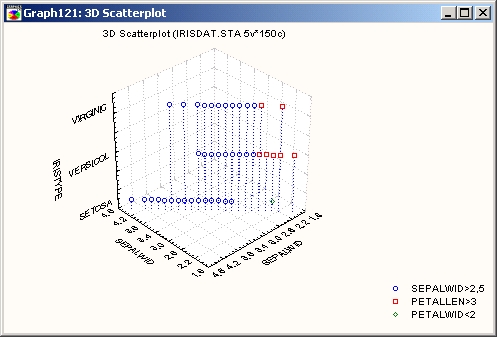
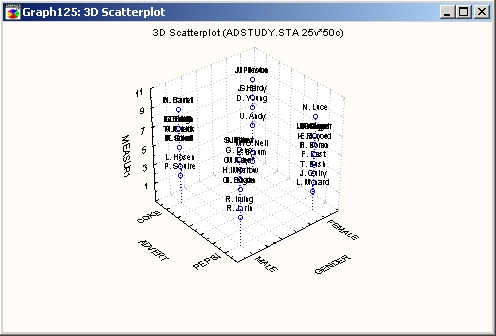
На приведенном выше графике, где подмножества маркированы, легко выделить различные виды ирисов.
Изучение результатов многомерного анализа
Часто XYZ диаграммы рассеяния используются в статистике для наглядного представления результатов многомерных методов исследования, таких как факторный анализ и многомерное шкалирование. Например, построение на трехмерном графике наблюдений с метками, являющихся трехмерным решением задачи многомерного шкалирования, может помочь в определении величин и классификации отдельных наблюдений.
Вращение
Общая проблема трехмерных диаграмм рассеяния — перекрывающиеся точки, которые затрудняют изучение графика. В некоторых случаях при очень большом числе наблюдений график почти невозможно понять, если смотреть на него под одним углом зрения. Поэтому при исследовании таких трехмерных графиков особенно полезно показанное ниже интерактивное вращение изображения на экране.
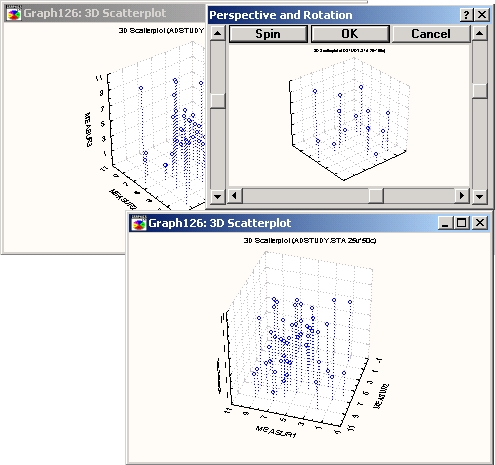
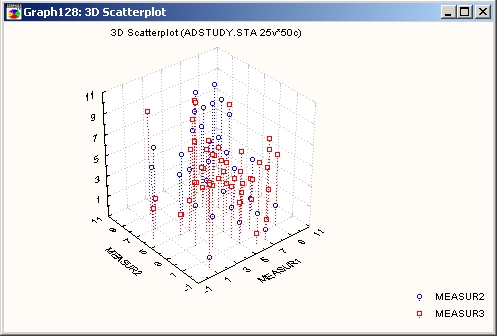
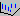 Диаграмма рассеяния
Диаграмма рассеяния
Этот простой тип XYZ диаграммы рассеяния отражает взаимосвязь между тремя или более переменными в трехмерном пространстве, при этом каждой точке соответствует тройка координат X, Y и Z.
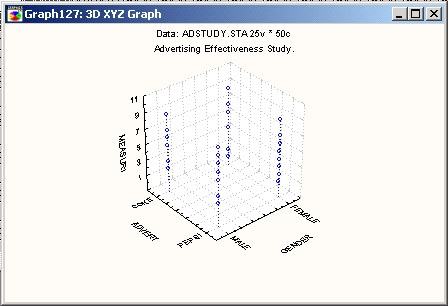
Заметьте, если выбрано более одной переменной Z, то будет построено несколько XYZ диаграмм рассеяния для различных наборов данных (соответствующих нескольким переменным Z), которые будут маркированы разными значками.
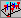 Пространственный график
Пространственный график
С помощью этого графика можно реализовать различные способы представления ЗМ диаграммы рассеяния. Для этого предусмотрена возможность расположения плоскости Х- Y на выбранном пользователем уровне вертикальной оси Z (которая проходит через середину плоскости).
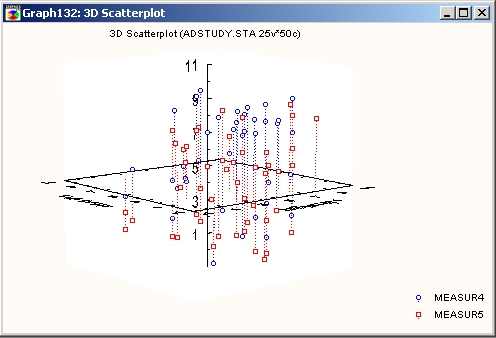
Хотя пространственные графики используются для тех же типов данных, что и XYZ диаграммы рассеяния, их представление может облегчить исследование некоторых трехмерных наборов данных. Рекомендуется сопоставлять данные отдельным осям на графике таким образом, чтобы переменную, структуру связей которой необходимо выделить, обозначить как Z. Тогда, перемещая плоскость XY вдоль оси Z и интерактивно вращая изображение, можно попробовать найти такой уровень Z, на котором изменяется структура связей между Х и Y (или Х, Y и Z).
Если ожидаемое изменение структуры слишком сложно для его исследования в одном «сечении», можно воспользоваться спектральным графиком, который позволяет наблюдать несколько сечений. Однако поскольку на спектральных графиках представлен набор двухмерных сжатых изображений трехмерных данных, здесь могут быть потеряны некоторые действительные трехмерные характеристики, которые наблюдаются на пространственных графиках.
Другое приложение пространственных графиков — наглядное представление плотности и направленности отклонений от определенного уровня (уровня отклонений).
 Спектральная диаграмма
Спектральная диаграмма
Первоначально этот тип графиков применялся в спектральном анализе для исследования нестационарных временных рядов, например, речевых сигналов. На горизонтальных осях можно откладывать частоты спектра и последовательные временные интервалы, а на оси Z — спектральные плотности для каждого интервала.
На этом типе графиков трехмерное пространство разделено на области, в которых данные «сжаты» в соответствующие спектральные плоскости. Обратите внимание, что для построения функциональных зависимостей (таких как в спектральном анализе) необходимо упорядочить данные таким образом, чтобы переменная Н содержала категоризующую информацию (то есть была группирующей переменной).
Спектральные диаграммы имеют явные преимущества перед обычными ЗМ диаграммами рассеяния, когда необходимо исследовать, каким образом изменяется взаимосвязь между двумя переменными при различных значениях третьей переменной. Это преимущество ясно видно на приведенных ниже двух изображениях одного и того же набора данных.
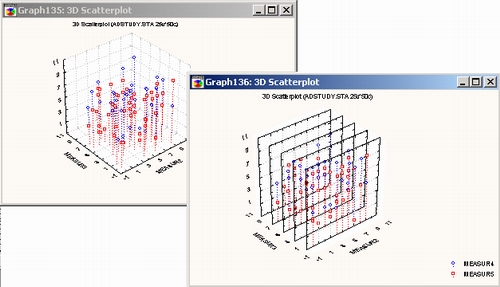
Значения переменных X и Z интерпретируются как координаты X и Z каждой точки, а значения переменной Y разделены на равноотстоящие группы, соответствующие положениям последовательных спектральных плоскостей.

Число спектральных плоскостей можно задать в поле редактирования Число плоскостей диалогового окна параметров графика или после построения графика в диалоговом окне ЗМ графики: дополнительные свойства.
Спектральные графики имеют два основных применения. Первое из них — это исследование функций или последовательно распределенных величин в трехмерном пространстве (например, график спектральных плотностей, определенных для последовательных интервалов времени).
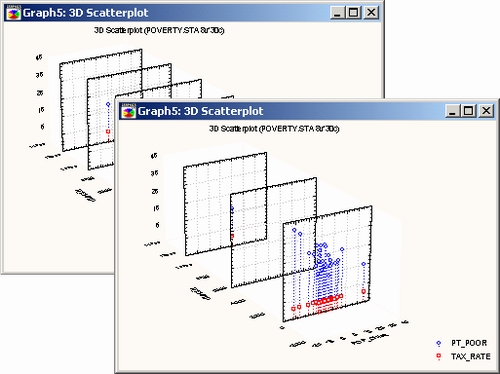
В то же время спектральные диаграммы являются «действительно трехмерными», а не последовательными графиками, и на них могут быть представлены три переменные, содержащие не равноотстоящие данные (например, периодограммы с упорядоченными по времени, но не равными интервалами).
Другое применение данных графиков — «расслоение» (или «сжатие») диаграмм рассеяния для выявления скрытых структур при разведочном анализе данных.

Если предполагается согласованная взаимосвязь между тремя переменными и особенно если ожидается, что связь между двумя переменными (X и Z) различна на разных уровнях третьей переменной (Y), то для исследования этого явления вполне можно использовать спектральные графики. Упростить анализ поможет выбор числа спектральных плоскостей (см. выше) и интерактивное вращение.
Заметим, что практически такой же ряд двухмерных изображений можно получить с помощью категоризованных графиков рассеяния, где Х и Z — отображаемые переменные, a Y — категоризующая переменная, разбитая на несколько интервалов (число которых равно числу спектральных плоскостей). Если вас интересуют подробности расположения данных на отдельных спектральных плоскостях, то проще использовать категоризованные диаграммы рассеяния (по сравнению с трехмерными спектральными графиками). Однако с помощью таких Категоризованных графиков нельзя получить цельное трехмерное представление исследуемых данных, которое может быть полезно для понимания их структуры.
Спектральные диаграммы можно использовать для исследования однородности, поскольку такое свойство, как однородность, трудно изучать на других типах графиков (например, можно исследовать зависимость дисперсии от значений переменной У или распределения выбросов).
 Диаграмма отклонений
Диаграмма отклонений
На этом типе графиков точки данных (заданные координатами X, Y и Z) представлены в виде «отклонений» от определенного базового уровня на оси Z.
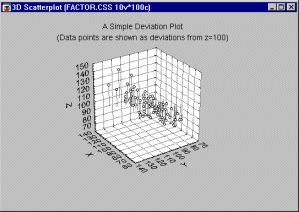
Диаграммы отклонений похожи на пространственные графики. Однако на них в отличие от последних «плоскость отклонений» «невидима» и не обозначена положением плоскости Х-Y (эти оси здесь всегда находятся в стандартном нижнем положении). С помощью диаграммы отклонений можно исследовать природу трехмерных наборов данных, изображая их в виде отклонений от произвольного (горизонтального) уровня. Как упоминалось выше, такой метод «сечения» может выявить динамические связи между исследуемыми переменными.
Для построения поверхности используется подгонка по точкам трехмерного графика рассеяния. Такое представление, как и ЗМ диаграммы рассеяния, позволяет выявить скрытую структуру данных и взаимосвязи между тремя переменными.
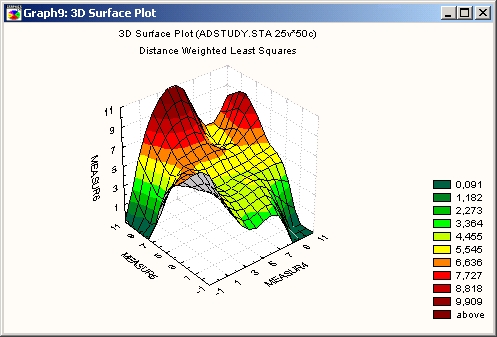
Графики поверхности используются в разведочном анализе данных, как и описанные в предыдущем разделе трехмерные диаграммы рассеяния. Кроме того, они полезны для наглядного представления результатов анализа, таких как подгонка пользовательской функции или кластерный анализ.
В промышленной статистике графики поверхности обычно используются для представления центрального композиционного плана эксперимента. Здесь экспериментатором задаются конкретные систематические значения двух (или более) переменных для оценки их влияния на некоторые зависимые переменные, представляющие интерес (например, прочность синтетической ткани).
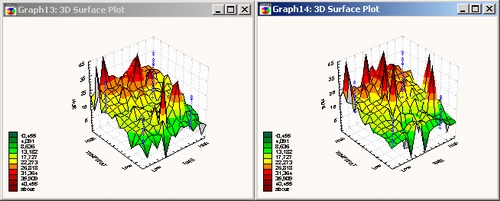
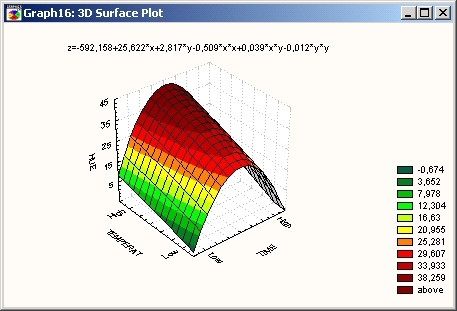
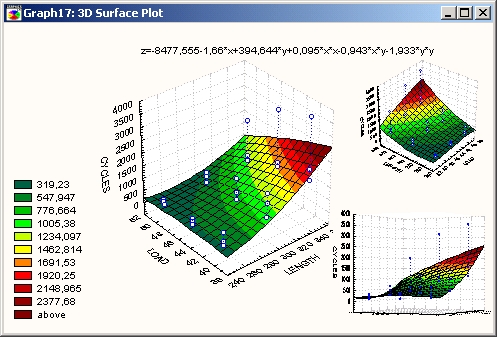
С помощью таких экспериментов можно обнаружить сложные нелинейные взаимосвязи между переменными.
Часто такой график бывает полезно вращать для более явного проявления характеристик поверхности (например, конкретных выпуклостей и впадин) или скрытых сторон.
 Линейное сглаживание
Линейное сглаживание
Трехмерная диаграмма рассеяния аппроксимируется линейной функцией (например, Z = а + bХ + сY).
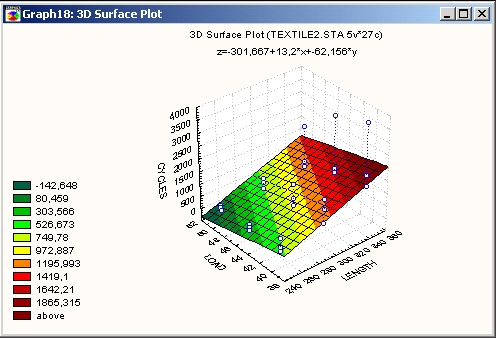
 Квадратичное сглаживание
Квадратичное сглаживание
Трехмерная диаграмма рассеяния аппроксимируется полиномом второго порядка.
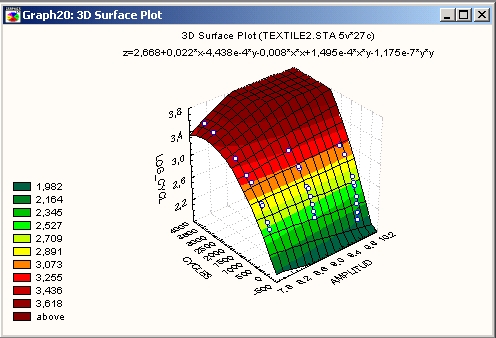
 Сглаживание методом наименьших квадратов
Сглаживание методом наименьших квадратов
Поверхность аппроксимируется методом наименьших квадратов с весами, зависящими от расстояния (влияние отдельных точек уменьшается с расстоянием до поверхности).
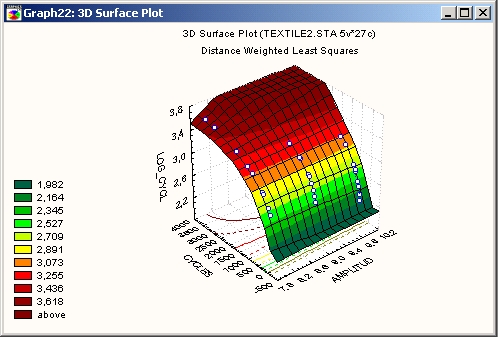
 Экспоненциально взвешенное сглаживание с отрицательным показателем
Экспоненциально взвешенное сглаживание с отрицательным показателем
Поверхность аппроксимируется в координатах XYZ методом экспоненциально взвешенного сглаживания с отрицательным показателем (влияние каждой точки экспоненциально уменьшается с расстоянием до поверхности).
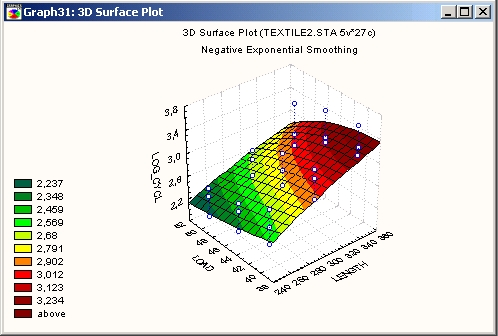
 Сглаживание сплайнами
Сглаживание сплайнами
Поверхность в координатах XYZ аппроксимируется бикубическими сплайнами.
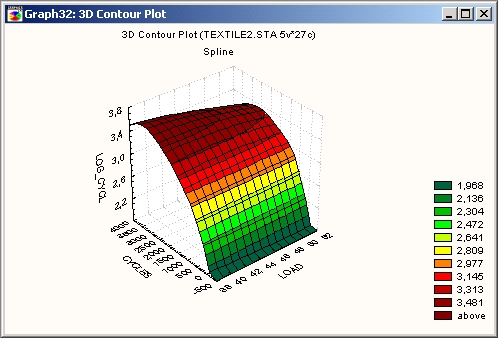
 Другая функция
Другая функция
Можно самостоятельно задать математическое выражение для описания поверхности.
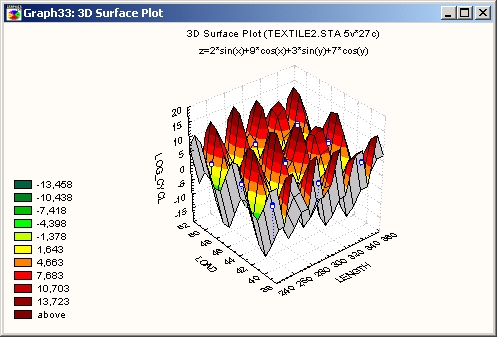
Обратите внимание, что заданная таким образом поверхность не будет аппроксимировать данные, а будет просто нарисована поверх них.
Карты линий уровня создаются путем подгонки трехмерной функции поверхности к трехмерной диаграмме рассеяния. Получившиеся в результате контурные линии (то есть линии равной «высоты») проектируются на плоскость Х- Y.
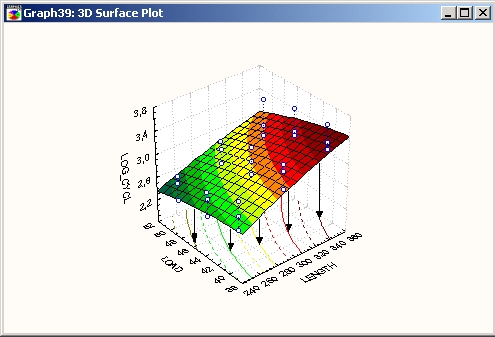
Подобно графикам поверхности, карты линий уровня используются для выявления взаимосвязей между тремя переменными.
Как и графики, описанные в предыдущих пунктах (трехмерные диаграммы рассеяния и поверхности), карты линий уровня находят свое применение в исследовательском анализе данных.

Кроме того, они полезны для наглядного представления результатов исследований, таких как подгонка пользовательской функции. Они менее эффективны по сравнению с графиками поверхности (описанными ранее) для быстрого наглядного представления полной пространственной структуры данных. Однако преимущество состоит в том, что карты дают возможность с большой точностью исследовать форму поверхности. Карты линий уровня представляют собой серию неискаженных горизонтальных «сечений» поверхности.
Как и на ЗМ диаграммах рассеяния, каждая точка данных на трассировочных графиках располагается в трехмерном пространстве в соответствии со значениями переменных X, Y и Z (которые интерпретируются как координаты). Затем эти точки последовательно соединяются линией (в соответствии с их расположением в файле данных), чтобы показать «след» (трассу) какого-либо процесса (например, движения, изменения чего-либо со временем и т. п.).
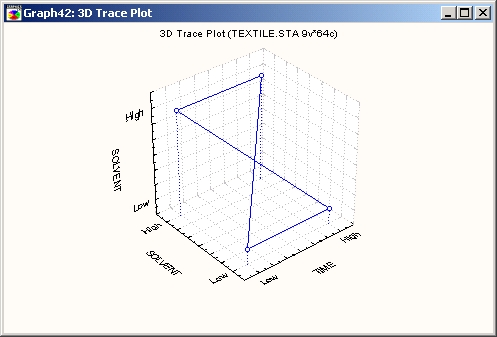
Наилучшим примером трассировочного графика является траектория объекта в трехмерном пространстве.
В общем случае с помощью трассировочных графиков можно изучать процессы, при которых переменные изменяются одновременно в трех измерениях при последовательном наблюдении.
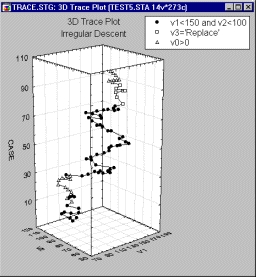
Отличие нескольких трассировочных графиков состоит только в том, что на них можно отображать одновременно ряд «траекторий» для списка переменных Z.
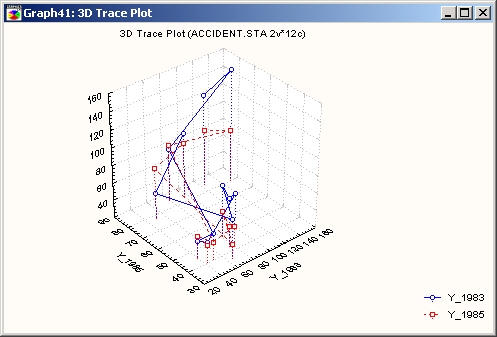
Примером набора данных, который можно сравнить с траекторией, служит любой многомерный временной ряд. Предположим, в большом городе каждый месяц в течение нескольких лет измерялись температура, уровень загрязнения и содержание озона в воздухе. Так как эти переменные по своей природе цикличны (например, зимой в северном полушарии холодно), то возникает характерная картина, которая в то же время имеет сложную структуру. С помощью таких графиков можно также изучать зависимость от времени цен на товары или макроэкономических показателей.
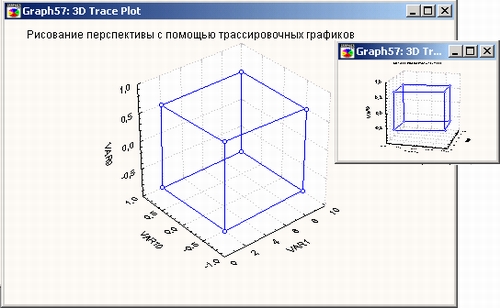
Другое приложение таких графиков — это создание точных «трехмерных рисунков» (с помощью задания координат в трехмерном пространстве) для таких объектов, как границы контроля или выделенные области. Обычно трехмерные объекты, нарисованные с помощью трассировочных графиков, можно вращать и изменять в перспективе. Обратите внимание, что такие объекты не могут быть нарисованы в интерактивном режиме, поскольку не существует способа контроля третьей размерности («глубины»).
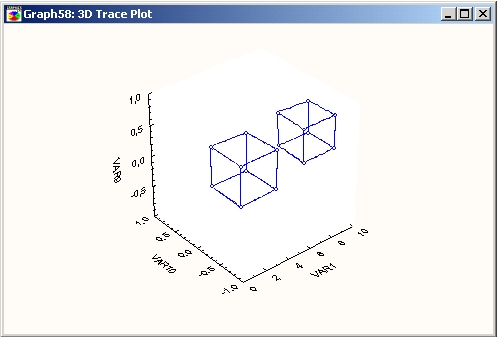
Если какое-либо наблюдение содержит пропущенные данные (например, не все три координаты X, Y и Z, а только две из них), то линия трассировочного графика будет разорвана. Это свойство можно использовать для создания отдельных объектов (как показано ниже).
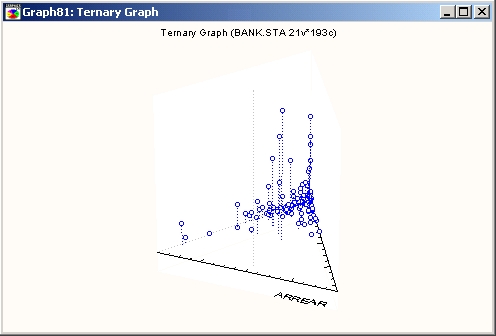
Тернарные графики используются для исследования связей между несколькими переменными, когда сумма значений переменных постоянна для всех наблюдений. Обычное такие графики применяются при экспериментальном исследовании зависимости отклика от относительного содержания трех компонент смеси (например, трех химических соединений), при этом соотношение компонент изменяется с целью определения его оптимального значения.
На тернарных графиках для построения зависимости четырех (или более) переменных (компонент X, Y и Z и откликов V1, V2 и т. д.) используется треугольная система координат на плоскости (тернарные диаграммы рассеяния или линии уровня) или в пространстве (тернарные трехмерные диаграммы рассеяния или поверхности). При построении тернарного графика относительная доля каждой компоненты (для каждого наблюдения) ограничена их общей постоянной суммой (например, 1). При создании графика масштаб долей по умолчанию изменяется таким образом, чтобы эта сумма была равна 1 для каждого наблюдения.
Предположим, имеется смесь, состоящая из трех компонент А, В и С. Любая трехкомпонентная смесь может быть обозначена точкой в треугольной системе координат, заданной тремя переменными.
Например, возьмем 6 следующих трехкомпонентных смесей:
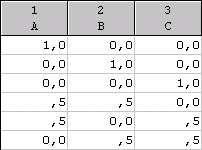
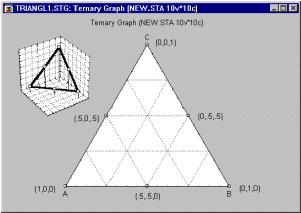
Сумма компонент в каждой смеси составляет 1,0, и эти значения могут рассматриваться как доли. Если отобразить эти данные на обычной трехмерной диаграмме рассеяния, то окажется, что они образуют треугольник в пространстве. Правильной смеси будут соответствовать только точки, находящиеся внутри треугольника, где сумма значений компонент равна 1. Поэтому для отображения соотношений компонент достаточно просто построить треугольник на плоскости.
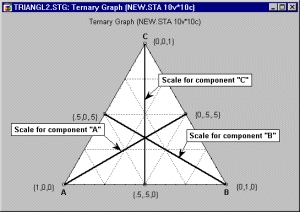
Три компоненты представлены осями, которые проходят из вершины треугольника до середины противоположного основания (медианами треугольника), и положение каждой точки определяется значениями, отложенными по соответствующим осям. Присмотревшись к графику, вы легко заметите, что в вершинах треугольника имеется лишь одна ненулевая компонента смеси, тогда как на сторонах треугольника — две компоненты не равны нулю, а одна компонента нулевая.
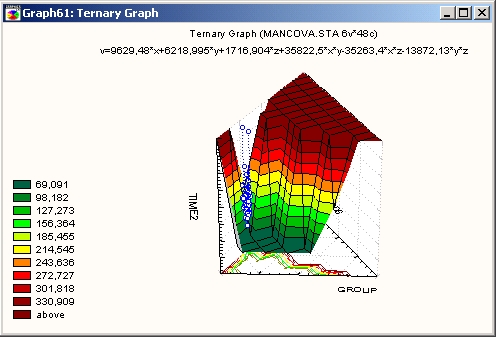
Тернарные графики можно проиллюстрировать следующим примером, рассмотренным в работе Вайнера (Wainer, 1995).
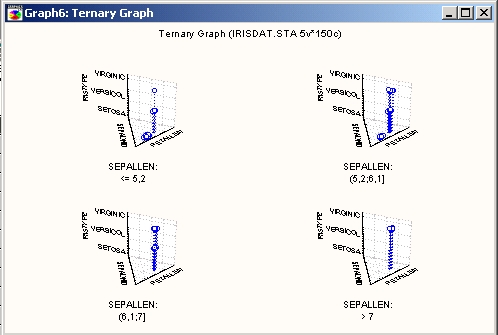
Тесты Национального бюро по развитию образования (National Assessment of Educational Progress (NAEP)) для студентов показали наличие трех уровней образованности: Высшее/Профессиональное (Advanced/Proficient), Среднее (Basic) и Неполное среднее (Below Basic). Результаты, полученные в различных регионах, могут быть изображены на тернарном графике, где по каждой из трех осей отложена доля студентов соответствующего уровня образованности.
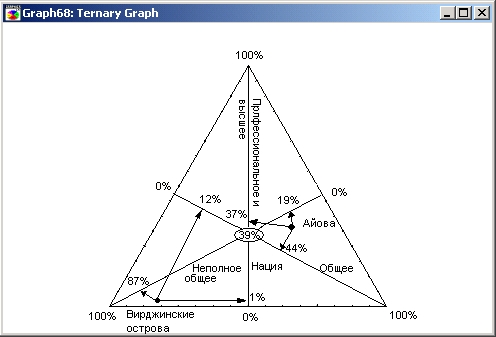
На показанном выше графике (Wainer, 1995) видно, что 37% студентов штата Айова (Iowa) имеют Высшее (Advanced) или Профессиональное (Proficient) образование, 44% — Среднее (Basic) и 19% — Неполное среднее (Below Basic). Для сравнения, только 1% студентов Вирджинских островов (Virgin Islands) имеют Высшее (Advanced) или Профессиональное (Proficient) образование, 12% — Среднее (Basic) и 87% — Неполное среднее (Below Basic).
Вайнер также обсуждает другое интересное применение графиков в треугольных координатах. Подобный график был использован для изучения доли голосов, отданных за каждую из трех британских политических партий на всеобщих выборах в 1987 и 1992 годах. Заинтересованные читатели найдут подробную информацию в работе: Wainer (1995). Visual revelations, Chance, 8, p. 48-54.
 2М диаграмма рассеяния
2М диаграмма рассеяния
На этих графиках треугольная система координат используется для построения зависимости трех (или более) переменных (компонент X, Y и Z) на плоскости.
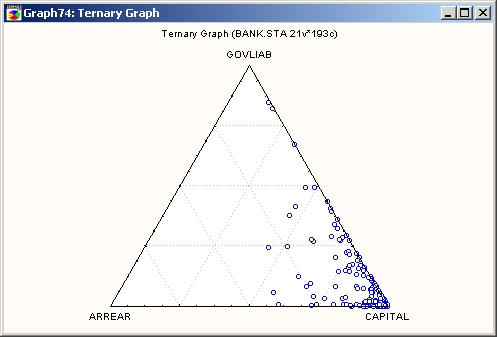
На приведенном графике изображены точки, соответствующие долям переменных-компонент (X, Y и Z).
 ЗМ диаграмма рассеяния
ЗМ диаграмма рассеяния
На этом типе тернарных графиков в треугольной системе координат в трехмерном пространстве строится зависимость четырех (или более) переменных (компонент X, Y и Z откликов V1, V2 и т. д.) — тернарные трехмерные диаграммы рассеяния или графики поверхности.
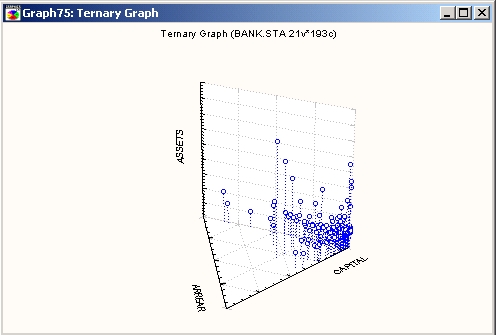
На этом тернарном графике отклики (V1, V2 и т. д.), соответствующие определенным долям переменных-компонент (X, Y и Z), откладываются в виде высот точек.
 Поверхность
Поверхность
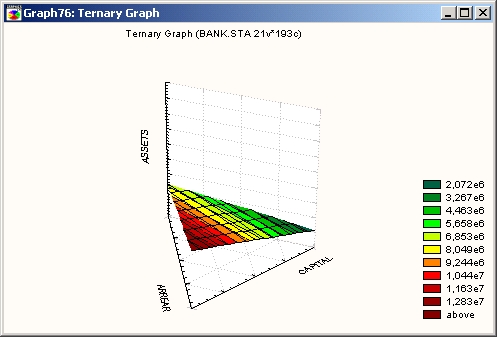
Здесь на трехмерном тернарном графике поверхность представляет собой результат подгонки к набору данных из четырех координат.
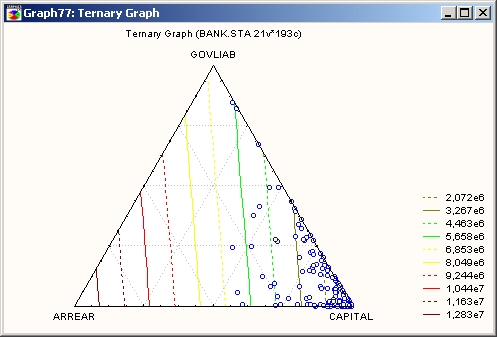
 Карта линий
Карта линий
В данном типе тернарных графиков трехмерная поверхность (подогнанная к набору данных из четырех координат) проектируется на плоскость в виде линий уровня.
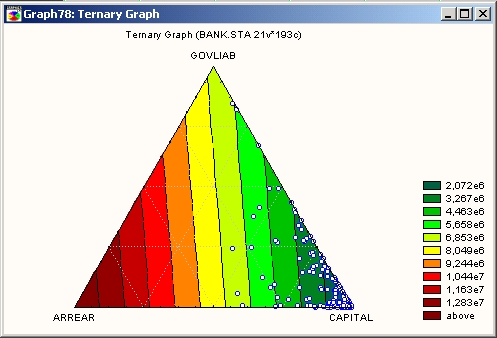
 Зонная карта
Зонная карта
На этом типе тернарных графиков трехмерная поверхность (подогнанная к набору данных) проектируется на плоскость в виде карты зон.
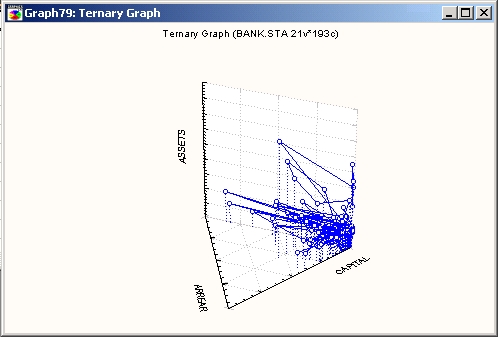
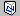 Трассировочный график
Трассировочный график
В данном случае можно исследовать связи между четырьмя и более переменными (X, Y,Z и V1, V2 и т. д.) с помощью соединения точек на графике в той последовательности, в какой они расположены в файле данных.
Кроме перечисленных выше вариантов, после построения графика в диалоговом окне Общая разметка можно также выбрать следующие типы графиков.
 Пространственный график
Пространственный график
Этот тип тернарных графиков предлагает особенный метод представления трехмерных диаграмм рассеяния с использованием плоскости Х- Y-Z (определенной в треугольной системе координат), которая располагается на заданном пользователем уровне вертикальной оси У (эта ось проходит через середину плоскости).
Уровень расположения плоскости Х- Y-Z можно подобрать таким образом, чтобы разделить пространство X-Y-Z на значимые части (например, для выделения различной структуры связей переменных).
 Диаграмма отклонений
Диаграмма отклонений
Эта диаграмма похожа на пространственный график, но на ней не отображается плоскость, от которой отсчитываются отклонения.

Подгонка
Приведенные ниже четыре уравнения регрессии можно использовать для подгонки зависимостей на тернарных графиках. Обратите внимание, что уравнения получены из стандартных полиномов с учетом ограничения на значения компонент (X, Y, Z), сумма которых для каждого наблюдения равна постоянной величине (например, 1,0).
Простейшая модель первого порядка:
V = a + bl×X + b2×Y + b3×Z
с ограничением X+Y+Z=1, может быть построена с помощью умножения коэффициента а на 1=X+Y+Z:
V = a×X + a×Y + a×Z + bl×X + b2×Y + b3×Z
Это выражение можно упростить:
V = (а+b1)×X + (а+Ь2)×Y +(а+bЗ)×Z
или записать таким образом:
V=bl'×X + b2'×Y + b3'×Z
Ниже перечислены доступные в STATISTICA функции полиномиальной регрессии:
V = bl×X + b2×Y + b3×Z
V = b1×X + b2×Y + bЗ×Z + b12×X×Y + b13×X×Z + b23×Y×Z
V = bl×X + b2×Y + b3×Z + bl2×X×Y + bl3×X×Z + b23×Y×Z + bl2×X×Y×(X-Y) + b1З×X×Z×(X-Z) + b23×Y×Z×(Y-Z) + b123×X×Y×Z
V=bl×X+b2×Y + b3×Z+bl2×X×Y + bl3×X×Z+b23×Y×Z + bl23×X×Y×Z
Трехмерные категоризованные графики
Этот тип статистических графиков позволяет создавать трехмерные категоризованные диаграммы рассеяния (и трассировочные графики), карты линий уровня и поверхности. При этом используются заданные категории выбранной переменной или другие способы логической группировки наблюдений.
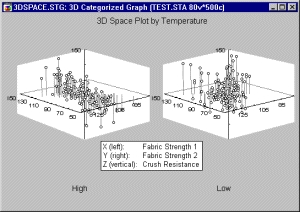
На графике представлена та же информация, что и на трехмерном графике рассеяния, графике поверхности или карте линий уровня, за исключением того, что здесь для каждой заданной пользователем группы или категории показан свой график. Основной смысл таких графиков — упростить сравнение групп или категорий, отражающих связи между тремя или более переменными.
В общем случае трехмерные XYZ графики отображают динамические связи между тремя переменными. С помощью различных способов категоризации данных можно исследовать связи в определенных группах данных.
Например, положительная взаимосвязь между возрастом, состоянием здоровья и удовлетворенностью жизнью наблюдается при опросе женщин, но не мужчин.
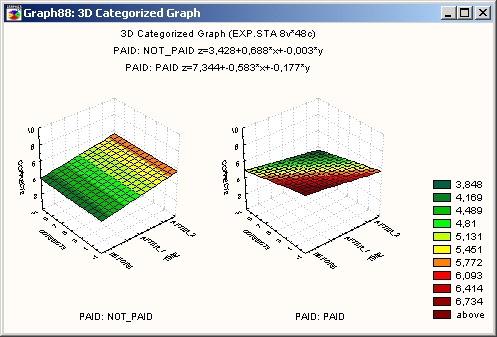
Поскольку категории создаются с помощью логических условий, которые определяют подгруппы, то можно пойти дальше и построить другие графики — разделив группу мужчин на одиноких или разведенных и женатых, можно выделить в отдельную группу одиноких мужчин с высокими доходами и т. п.
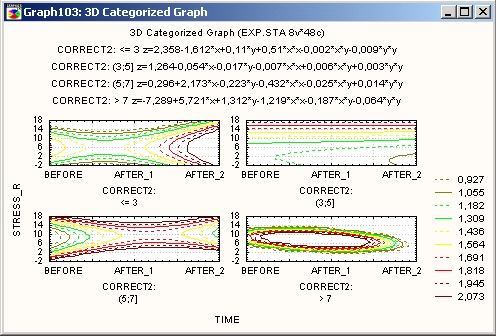
Из приведенных ниже категоризованных графиков поверхности (и соответствующих им карт линий уровня) можно сделать заключение о том, что задание величины допусков на приборе не влияет на исследуемую взаимосвязь между результатами измерений (Dependl, Depend2 и Height), за исключением случаев, когда эта величина <3.

Иногда карты линий уровня легче анализировать, чем графики поверхности (что хорошо видно из следующего примера).
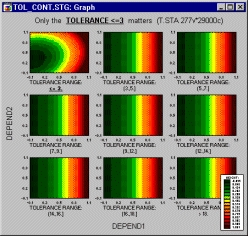
Таким образом, ЗМ категоризованные графики представляют собой мощный исследовательский инструмент для изучения сложных взаимосвязей между переменными и группами наблюдений.
 Категоризованная ЗМ диаграмма рассеяния
Категоризованная ЗМ диаграмма рассеяния
На этом типе графиков отображаются связи между тремя переменными (представляющими координаты X, Y и Z (вертикаль) в трехмерном пространстве), разделенными на категории с помощью группирующей переменной или путем задания подгрупп.

 Категоризованный пространственный график
Категоризованный пространственный график
В данном случае в одном графическом окне строится несколько пространственных графиков (для групп категоризованных данных).
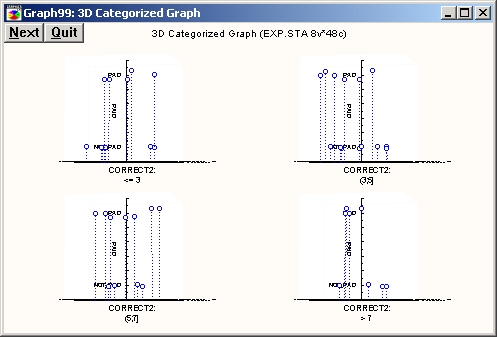
 Категоризованная спектральная диаграмма
Категоризованная спектральная диаграмма
На этом типе графика трехмерное пространство разделено на области, в которых данные «сжаты» в соответствующие спектральные плоскости.
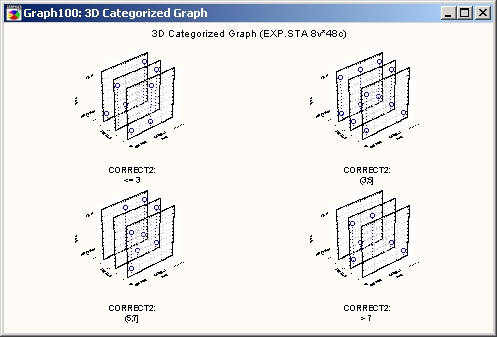
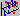 Категоризованная диаграмма отклонений
Категоризованная диаграмма отклонений
На этом типе графиков точки данных (заданные координатами X, Y и Z) представлены в виде «отклонений» от определенного базового уровня на оси Z.
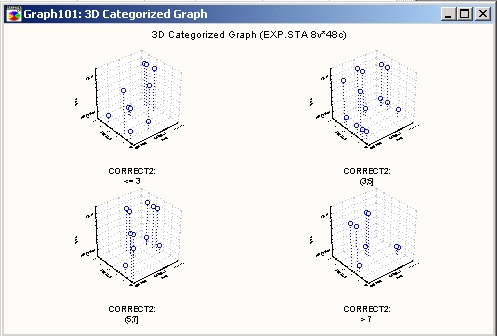
 Категоризованный график поверхности
Категоризованный график поверхности
С помощью этой функции будет построена поверхность (методом сглаживания или по заданному математическому выражению) для категоризованных данных.
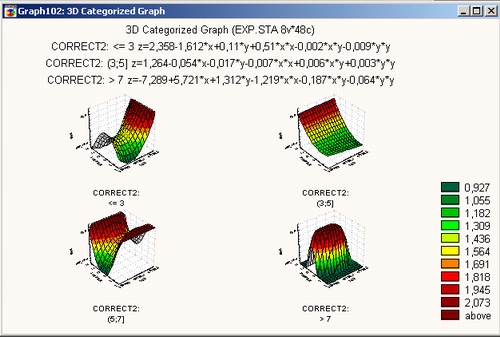
 Карта линий уровня
Карта линий уровня
Карта линий уровня — это проекция трехмерной поверхности на двухмерную плоскость. На ней линиями обозначены одинаковые «высоты» (равные значения переменной Z).
 Зонная карта
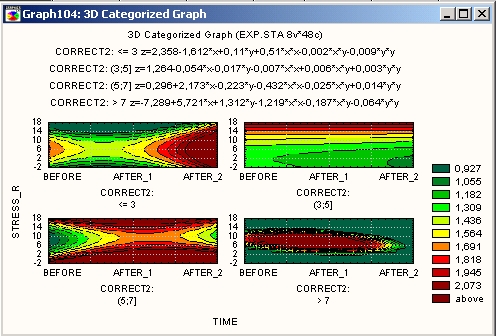
Зонная карта
На таком графике одинаковые «высоты» (значения переменной Z) на поверхности (зоны между контурными линиями одинаковой высоты, см. предыдущий тип графика) показаны областями одинакового цвета и вида.
Категоризованные тернарные графики
Катетеризованные тернарные графики используются для исследования взаимосвязей между тремя и более переменными, когда три из них представляют собой компоненты смеси для каждого значения группирующей переменной (то есть между ними существует жесткая связь, заключающаяся в том, что их значения в сумме дают постоянную величину для всех наблюдений).
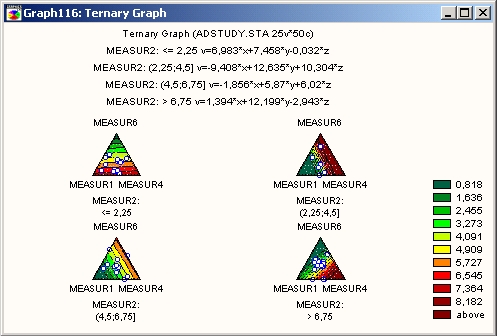
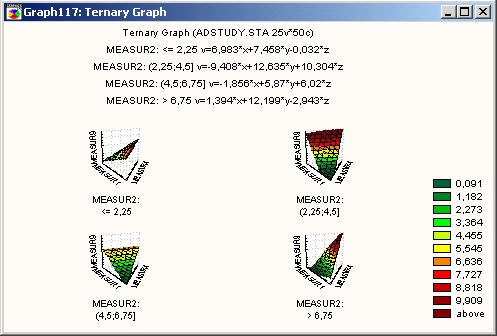
На тернарных графиках для построения зависимости четырех (или более) переменных (компонентов X, Y и Z и откликов V1, V2 и т. д.) используется треугольная система координат на плоскости (тернарные диаграммы рассеяния или линии уровня) или в пространстве (тернарные трехмерные диаграммы рассеяния или поверхности). При построении тернарного графика относительная доля каждой компоненты (для каждого наблюдения) ограничена их общей постоянной суммой (например, 1). По умолчанию при создании графика масштаб долей изменяется таким образом, что эта сумма для каждого наблюдения становится равной 1. В вершинах треугольника имеется только одно ненулевое значение компонент смеси.
На категоризованных тернарных графиках для каждого уровня группирующей переменной (или заданной пользователем подгруппы) строится отдельный график. Все эти графики располагаются в одном графическом окне для сравнения групп данных (категорий).
Обычно такие графики используются в экспериментах, где отклик зависит от относительного содержания трех компонент (например, трех различных химических соединений). Причем это соотношение варьируется с целью определения его оптимального значения (например, при исследовании смесей). Эти типы графиков могут быть также использованы в том случае, когда необходимо сравнить группы или категории данных при наличии жестко заданной связи между переменными.
 Категоризованная 2М диаграмма рассеяния
Категоризованная 2М диаграмма рассеяния
На таких графиках треугольная система координат используется для построения зависимости трех (или более) переменных (компонент X, Y и Z) на плоскости.
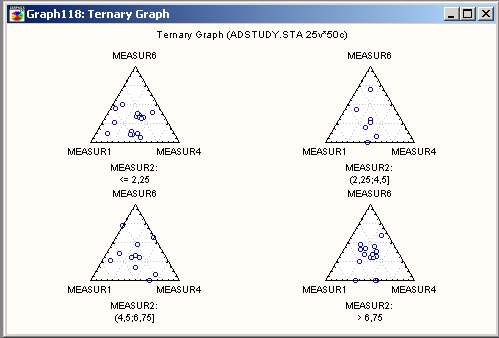
Здесь изображены точки, представляющие собой доли переменных-компонент (X, Y и Z).
 ЗМ диаграмма рассеяния
ЗМ диаграмма рассеяния
Для данного типа тернарных графиков в треугольной системе координат в трехмерном пространстве строится зависимость четырех (или более) переменных (компонент X, Y и Z и откликов V1, V2 и т. д.) (тернарные трехмерные диаграммы рассеяния или графики поверхности).
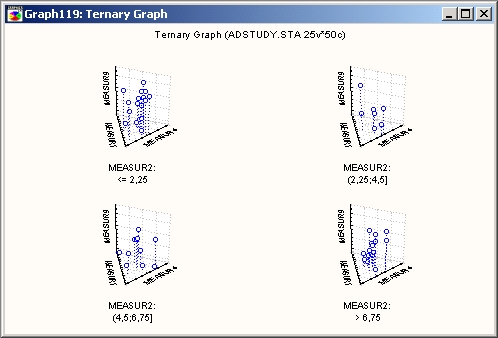
На этом тернарном графике отклики (V1, V2 и т. д.), соответствующие определенным долям переменных-компонент (X, Y и Z), откладываются в виде высот точек.
 Поверхность
Поверхность
Здесь на трехмерном тернарном графике поверхность представляет собой результат подгонки к набору данных из четырех координат.
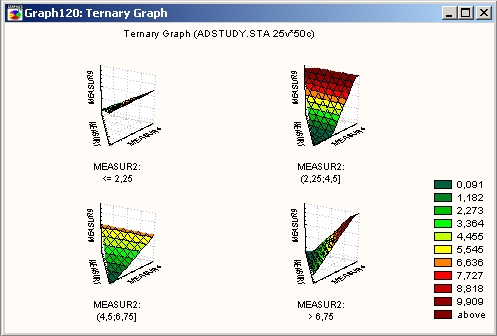
 Карта линий
Карта линий
В этом типе тернарных графиков трехмерная поверхность (подогнанная к 4 мерному набору данных) проектируется на плоскость в виде линий уровня.
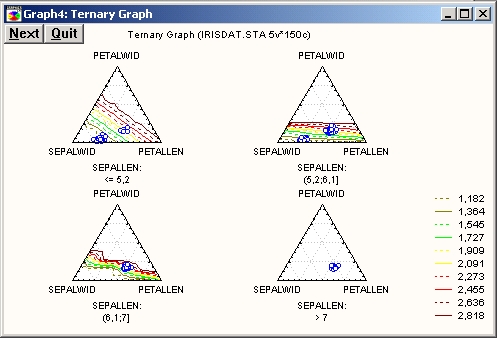
 Зонная карта
Зонная карта
В данном случае трехмерная поверхность (подогнанная к 4-координатному набору данных) проектируется на плоскость в виде карты зон.
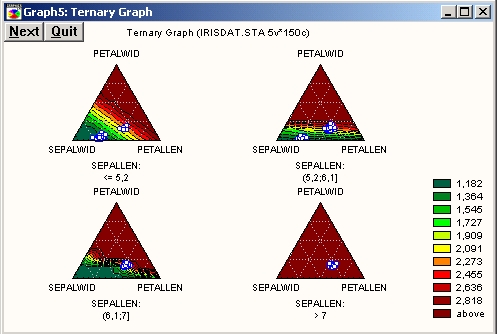
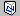 Трассировочный график
Трассировочный график
С помощью таких графиков можно исследовать связи между четырьмя и более переменными (X, Y, Z и V1, V2 и т. д.) путем соединения точек в той последовательности, в какой они расположены в файле данных.
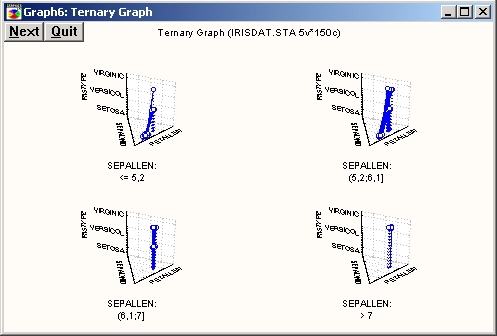
 Пространственный график
Пространственный график
Этот тип тернарных графиков реализует специальный метод представления трехмерных диаграмм рассеяния с использованием плоскости X-Y-Z (определенной в треугольной системе координат), которая располагается на заданном уровне вертикальной оси У(эта ось проходит через середину плоскости).
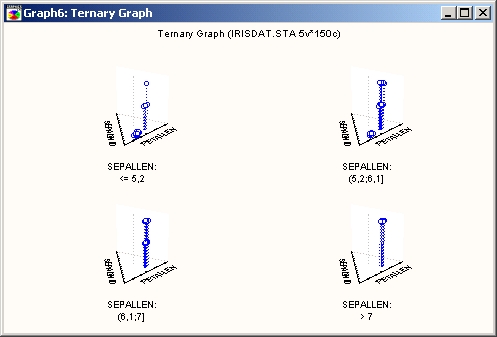
Уровень расположения плоскости Х- Y-Z можно подобрать таким образом, чтобы разделить пространство X-Y-Z нa значимые части (например, для выделения различной структуры связей переменных).
 Диаграмма отклонений
Диаграмма отклонений
Эта диаграмма похожа на пространственный график (см. выше), но на ней не отображается плоскость, от которой отсчитываются отклонения.
Подгонка
Приведенные ниже четыре уравнения регрессии можно использовать для подгонки данных на статистических, категоризованных или пользовательских тернарных графиках. Обратите внимание, что эти уравнения получены из стандартных полиномов с учетом ограничения на значения компонент (X, Y, Z), сумма которых для каждого наблюдения равна постоянной величине (например, 1,0). Например, простая модель первого порядка:
V = a + bl×X + b2×Y + b3×Z
с ограничением Х+ Y+Z= 1, может быть построена с помощью умножения коэффициента а на 1-X+Y+Z:
V = a×X + a×Y + a×Z + bl×X + b2×Y + b3×Z
Это выражение можно упростить:
V = (а+b1)×X+(а+b2)×Y+(а+bЗ)×Z
или записать таким образом:
V=b1'×Х + b2'×Y + b3'×Z
Ниже показаны доступные функции полиномиальной регрессии:
V = bl×X + b2×Y + b3×Z
V = bl×X + b2×Y + b3×Z + bl2×X×Y + bl3×X×Z + b23×Y×Z
V = bl×X + b2×Y + b3×Z + bl2×X×Y + bl3×X×Z + b23×YvZ + b12×X×Y×(X-Y) + b1З×X×Z×(X-Z)+ b23×Y×Z×(Y-Z)+b23×X×Y×Z
V = bl×X + b2×Y + b3×Z + bl2×X×Y + bl3×X×Z + b23×Y×Z + b123×X×Y×Z
Можно задать пользовательскую функцию. Однако такие функции не подгоняются к данным, а лишь накладываются на график.
Графики пользовательских функций
В отличие от других типов графиков, здесь не нужно выбирать переменные. Вместо этого программа попросит вас ввести формулу для построения графика. В этом режиме можно построить график не по значениям переменных файла данных, а по заданной пользователем формуле (то есть отобразить пользовательскую функцию), например:
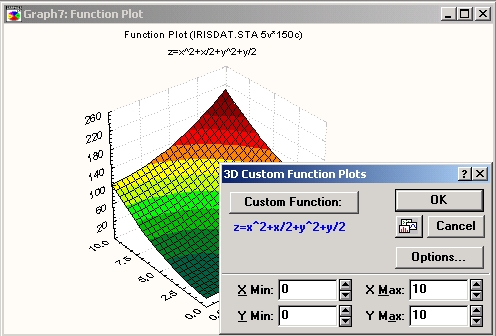
На данном типе графика можно в явном виде задать диапазон изменения переменных. Например, можно задать минимальное и максимальное значения для обеих осей (X и Y) равным соответственно 0 и 100.
Есть два основных варианта применения графиков функций, заданных пользователем.
Наиболее очевидный — исследование конкретной функциональной зависимости (например, проверка соответствия данных конкретной теоретической модели исследуемого процесса или явления).
Другое направление — это разведочный анализ данных, когда необходимо изучить форму функциональной зависимости в различных диапазонах значений аргумента.
Следующим шагом такого исследования, конечно, является статистическая проверка качества подгонки функции к конкретным данным.
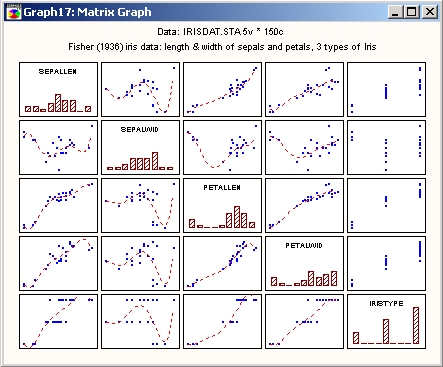
Матричные графики используются для графического представления зависимостей между переменными некоторого множества в виде матрицы обычных двухмерных графиков. Чаще всего в качестве матричных графиков используются диаграммы рассеяния, их можно рассматривать как метод визуализации корреляционных матриц исследуемых переменных.
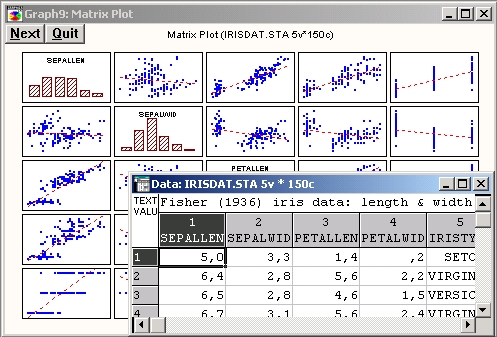
На приведенном графике для каждой пары переменных построена диаграмма рассеяния с изображенной на ней прямой линейной регрессии.
Матрицы диаграмм рассеяния могут быть не только квадратными (как на приведенном рисунке), но и прямоугольными, если были выбраны два списка переменных (по аналогии с прямоугольными матрицами корреляции). Если используется квадратная матрица, то на диагонали вместо диаграмм рассеяния будут построены гистограммы для соответствующих переменных.
Подобные графики предоставляют эффективный способ визуального анализа зависимостей между исследуемыми переменными. Например, с их помощью из набора переменных легко выделить переменные, которые не коррелируют с другими переменными.
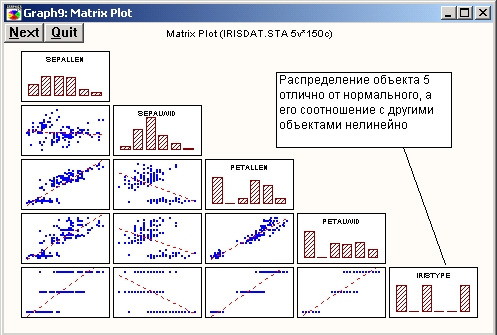
Матрицы линейных графиков
Рассмотренные выше матрицы диаграмм рассеяния обычно используются для графического представления зависимостей между некоторыми случайными переменными. Для изображения многоступенчатых процессов применяются, как правило, матрицы линейных графиков.
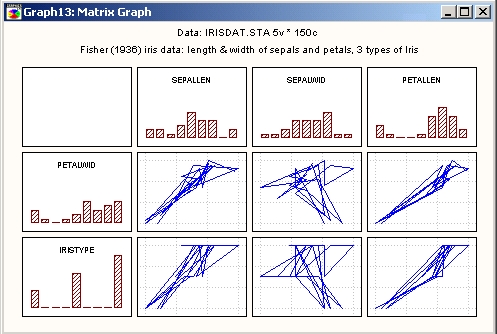
Например, на построенных матричных графиках изображено несколько различных зависимостей переменной Y (состояние процесса) от одной переменной X (времени); таким образом, на одном рисунке может быть построено сразу несколько изучаемых процессов (временных рядов).
Типичным применением матричных графиков является одновременное изображение на одном графике распределений анализируемых переменных и зависимостей между ними.

Это бывает полезно при выборе масштаба измерений или проведении разведочного анализа данных (например, обработка анкет, экономической информации, данных о контролируемом процессе и т. д.).

При проведении разведочного анализа данных бывает необходимо изучить влияние отдельных наблюдений, удовлетворяющих некоторому условию, на общий вид зависимости между переменными. Это можно сделать с помощью логических условий выделения подмножества наблюдений для построения матричного графика.

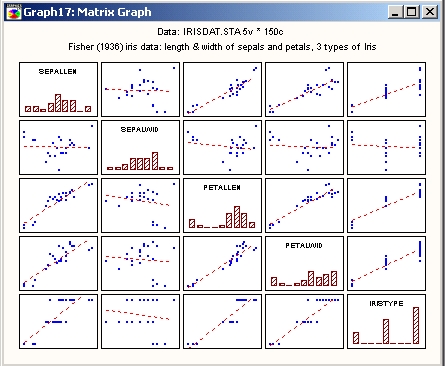
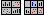 Матрица рассеяния
Матрица рассеяния
На этом матричном графике представлены двухмерные диаграммы рассеяния, на каждой из которых значения переменной из строки используются в качестве координат X, а значения переменных из столбца — в качестве координат Y.
Гистограммы, изображающие распределения каждой переменной, расположены на главной диагонали матрицы (в квадратных матрицах) или по краям (в прямоугольных матрицах).
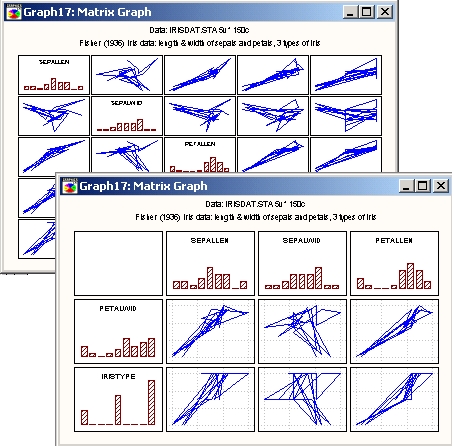
 Матрица линий
Матрица линий
При выборе этого типа графика создается матрица линейных (то есть непоследовательных) -XY-графиков (подобно матричной диаграмме рассеяния), на которых отдельные точки соединены линиями в порядке их появления в файле данных.
Гистограммы, изображающие распределения каждой переменной, располагаются на главной диагонали матрицы (в квадратных матрицах) или по краям (в прямоугольных матрицах).
 Матрица столбцов
Матрица столбцов
На этом графике матрица состоит из столбчатых диаграмм, на которых представлены проекции отдельных точек данных на ось X (показывающие распределение максимальных значений).
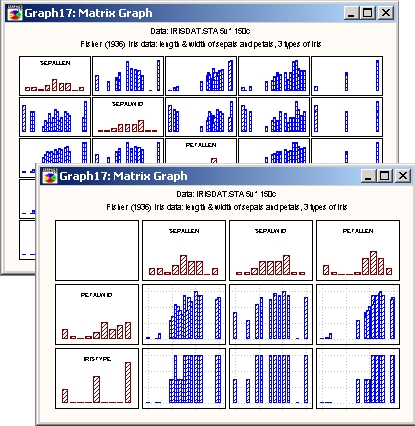
Гистограммы, изображающие распределения каждой переменной, расположены на главной диагонали матрицы (в квадратных матрицах) или по краям (в прямоугольных матрицах).
Подгонка функции к данным
 Линейная подгонка
Линейная подгонка
Линейная функция ( Y = а + bХ) подгоняется к точкам каждой двухмерной диаграммы рассеяния. Параметры а, b оцениваются методом наименьших квадратов. Заметьте, что прямая не проходит через наблюдаемые точки, а располагается максимально близко к ним (выбором a, b минимизируется сумма квадратов расстояний от точек до прямой). То же относится к другим линиям (см. ниже).
 Логарифмическая подгонка
Логарифмическая подгонка
К данным подгоняется логарифмическая функция вида:
Y = q×[lognх] + b,
где основание логарифма (п) выбирается пользователем (по умолчанию используется натуральный логарифм по основанию е, где е = 2,71...).
 Экспоненциальная подгонка
Экспоненциальная подгонка
По данным подбирается экспоненциальная функция вида:
у - b×exp(q×x)
 Подгонка сплайнами
Подгонка сплайнами
В данном случае производится сглаживание данных бикубическими сплайнами.
 Полиномиальная подгонка
Полиномиальная подгонка
Здесь методом наименьших квадратов данные аппроксимируются полиномом вида
у = b0 + b1×x +b2×х2 + b3×х3+...+ bn×xn,
где n есть степень полинома (1<n<6). Степень полинома может быть выбрана.
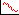 Подгонка методом наименьших квадратов
Подгонка методом наименьших квадратов
Кривая подгоняется к координатам данных с помощью процедуры сглаживания методом взвешенных относительно расстояния наименьших квадратов (влияние отдельных точек уменьшается с увеличением горизонтального расстояния от соответствующих точек на кривой).
 ЭкспМатричные графикионенциально взвешенное сглаживание.
ЭкспМатричные графикионенциально взвешенное сглаживание.
Кривая подгоняется к координатам X У данных с помощью процедуры экспоненциально взвешенного сглаживания с отрицательным показателем.

Влияние отдельных точек уменьшается с увеличением горизонтального расстояния от соответствующих точек на кривой.
|
|