Спектры непериодических сигналов конечной длительности (финитных), зарегистрированных на интервале Т, могут быть получены из уравнений для рядов Фурье как предельные значения функций суммирования при расширении периода Т до бесконечности.
Зададим периодическую последовательность импульсов и разложим импульс на одном периоде Т в ряд Фурье (формула 4.1.2). Не меняя положения импульса на интервале Т, увеличим значение Т в два раза (продлеваем интервал нулями), при этом выражение (4.1.2) для вычисления спектра остается без изменения, но по ней рассчитывается в 2 раза большее количество гармоник с уменьшением в 2 раза частоты первой гармоники и шага Dw=2p/T. Увеличение интервала Т не влияет на результаты вычисления интеграла функции (4.1.2), т.к. интервал продления заполнен нулевыми значениями сигнала.
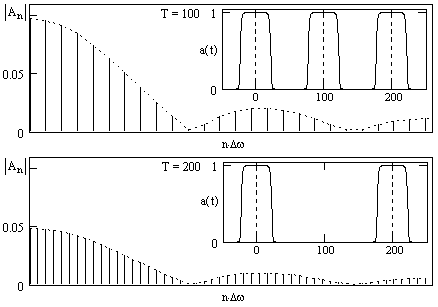
По существу, при увеличении периода Т без изменения финитного сигнала форма спектра по оси частот остается без изменения, изменяется только шаг дискретизации спектра и, за счет множителя 1/Т, в 2 раза уменьшаются значения спектра. Новые гармоники располагаются в интервалах между гармониками первого ряда. Пример изменения спектра при увеличении периода Т в 2 раза приведен на рис. 4.2.1.
Рис. 4.2.1.
Процесс можно продолжить дальнейшим последовательным увеличением периода, при этом спектр будет приближаться к непрерывной функции. В пределе, при T ® Ґ , периодическая последовательность импульсов заменяется одиночным финитным сигналом, дискретные частоты nDw обращаются в непрерывные текущие значения w (Dw = 2p/T ® 0), суммирование амплитудных значений заменятся интегрированием, а сами значения спектра становятся бесконечно малыми (1/Т® 0). Для исключения последнего множитель 1/Т из расчетной формулы S(w) исключается, и интегральное преобразование Фурье приобретает следующий вид:
s(t) = (1/2p)
S(w)exp(jwt) dw, (4.2.1)
S(w) =s(t)exp(-jwt) dt. (4.2.2)
Формулу (4.2.2) обычно называют формулой прямого преобразования Фурье, а формулу (4.2.1) – обратного преобразования Фурье. Этими выражениями устанавливается взаимно однозначная связь сигнала и его спектра, а точнее – плотности спектра сигнала в последовательной полосе малых (стремящихся к нулю) полосах частот. Эту величину называют спектральной плотностью сигнала. Спектральные функции содержат ровно столько информации, сколько и исходный сигнал.
При преобразовании сигнала в пространство гармонических частот и обратно формулы прямого и обратного преобразований Фурье тождественны за исключением знака аргументов экспоненты:
s(t) =S(f)exp(j2pft) df, (4.2.1')
S(f) =s(t)exp(-j2pft) dt. (4.2.2')
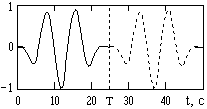
На рис. 4.2.2 сплошной кривой приведен пример непрерывного сигнала s(t), энергия которого сосредоточена на конечном интервале T = (0,25). Если нас не интересует форма данного сигнала за пределами интервала Т, то спектр сигнала в виде ряда Фурье можно определить по формуле (4.1.2). При обратном преобразовании Фурье по формуле (4.1.1), т.е. при восстановлении сигнала по его спектру, в интервале Т будет восстановлен исходный сигнал s(t). Но если интервал для восстановления будет задан больше интервала Т, например равным 0-2Т, то за пределами этого интервала начнется периодическое повторение исходного сигнала, как это показано пунктиром на рис. 4.2.2. Если такой процесс нежелателен и за пределами интервала Т должны быть сохранены нулевые значения сигнала, то необходимо использовать интегральное преобразование Фурье (4.2.1, 4.2.2). При этом следует учитывать особенности интегрального преобразования.
Спектральная функция S(w) представляет собой комплексную спектральную плотность сигнала, непрерывную на частотном интервале от - Ґ до Ґ . Если s(t) – вещественная функция, то спектр этой функции является сопряжено симметричным относительно нулевой частоты
S(-w) = S*(w)
и содержит четную действительную и нечетную мнимую части:
S(w) = A(w) - jB(w), (4.2.3)
A(w) =s(t)cos(wt) dt, (4.2.4)
B(w) =s(t)sin(wt) dt. (4.2.5)
Как и в случае рядов Фурье, вещественные четные функции имеют вещественный четный спектр, представленный только спектральной функцией A(w), а вещественные нечетные – нечетный и только мнимый спектр, представленный спектральной функцией B(w).
Пример спектральной функции S(f) для сигнала s(t) на рис. 4.2.2 приведен на рис. 4.2.3. Как правило, графическое отображение спектральных функций выполняется в виде модуля и аргумента спектральной функции (амплитудного и фазового спектра), приведенных на рис. 4.2.4.
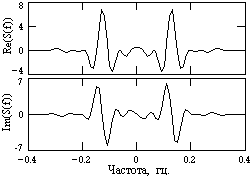
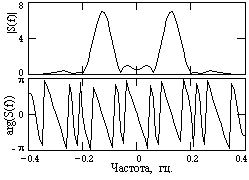
Рис. 4.2.3. Рис. 4.2.4.
Такое представление аналогично (4.1.3'):
R(w) =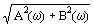 
, (4.2.6)
j(w) = arctg(-B(w)/A(w)), (4.2.7)
но в отношении функции модуля также имеет смысл спектральной плотности модуля.
Заметим также, что сопряженная симметричность спектральной функции позволяет в формулах (4.2.1)-(4.2.2) менять местами знаки аргументов в экспонентах, при этом изменяется только знак мнимой части и аргумента спектра.
Еще раз подчеркнем различие между спектрами и спектральными функциями сигналов. При практическом использовании формулы (4.2.2) для вычисления спектральных функций конечных сигналов, заданных на определенном интервале Т, пределы интегрирования обычно устанавливаются по границам интервала Т, так как нет необходимости выполнять интегрирование в бесконечных пределах, если за пределами интервала Т мы имеем нулевые (или незначимые) значения сигнала. Однако при сравнении формулы (4.2.2) с выражением (4.1.2) можно наглядно видеть, что значения интеграла (4.2.2) не нормируются на величину интервала Т. Отсюда следует, что числовые отсчеты значений модуля функции S(w) для определенных значений wi не являются амплитудными значениями соответствующих гармонических колебаний с частотой wi. Значения S(w) по сравнению со значениями функции S(nDw) по (4.1.2) при nDw = wi завышены на множитель Т. Это можно объяснить тем, что обратное преобразование Фурье по (4.1.1) представляет собой прямое суммирование гармоник с соответствующими амплитудами колебаний, в то время как интегрирование по (4.2.1) представляет собой предельное суммирование значений S(wi)Ч dwi, где dw = 2p/T (или, в обычном частотном представлении, df = 1/T) при Т Ю Ґ .
Что касается спектра фазовых углов, то значения по (4.2.7) и по (4.1.3') при nDw = wi полностью совпадают, так как их вычисление производится по отношению мнимой и действительной части спектра, наличие (или отсутствие) постоянного множителя в которых не меняет значение отношения.
Тригонометрическая форма интеграла Фурье (при объединении комплексно сопряженных частей спектральных функций):
s(t) = (1/2p) [A(w)cos(wt)+B(w)sin(wt)] dw. (4.2.8)
s(t) = (1/2p)R(w)cos(wt - j(w)) dw. (4.2.8')
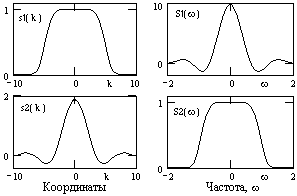
Прямое и обратное преобразование Фурье подобны. Любая теорема, доказанная для прямого преобразования Фурье, справедлива и для обратного преобразования, и наоборот. Это непосредственно следует из выражений прямого и обратного преобразования Фурье, которые различаются только знаком в экспоненте. Особенно наглядно (см. рис. 4.2.5) это видно для четных сигналов (заданных функциями, симметричными относительно t = 0), для которых В(w) = 0 и, соответственно, фазовый спектр равен нулю:
s(t) = 2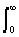
S(f)cos(2pft)df, S(f) = 2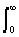s(t)cos(2pft)dt.
В математическом анализе для упрощения записей используют символическую форму обозначения преобразования Фурье:
s(t) Ы S(f), s(t) Ы S(w),
где, в общем случае, как фурье-образ функции, так и она сама могут быть комплексными.
Для физических сигналов и их достаточно корректных математических моделей преобразование Фурье, как правило, всегда существует. С чисто математических позиций сигналу s(t) можно сопоставить спектральную плотность S(w), если существует интеграл:
|s(t)| dt < Ґ . (4.2.9)
Если условие (4.2.9) не выполняется, то определенные приближения спектральных плотностей вычисляются с использованием специальных методов, одним из которых является преобразование Лапласа.
Допустим, что функция s(t) задана на интервале (0, Ґ ), равна нулю при t<0, а интеграл спектральной функции (4.2.2) расходится. Умножим s(t) на экспоненциальную функцию exp(-ct), где с - положительная константа, и выберем значение 'с' таким, чтобы произведение u(t) = s(t)Ч exp(-ct) удовлетворяло условию абсолютной интегрируемости. Сущность данной операции хорошо видна на рис. 4.2.6. Интегрируемость функции u(t) может быть установлена для любой функции s(t) соответствующим выбором коэффициента 'c'. При этом спектральная плотность функции u(t) может быть вычислена по формуле (4.2.2):
U(w,c) =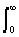[s(t) exp(-ct)] exp(-jwt) dt.
После объединения экспоненциальных функций это выражение можно переписать следующим образом:
U(c+jw) =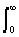s(t) exp[-(c+jw)t] dt. (4.2.10)
Соответствующее обратное преобразование Фурье функции U(c+jw):
(1/2p)S(c+jw) exp(jwt) dw = s(t) exp(-ct).
Для восстановления функции s(t) достаточно умножить обе части данного выражения на exp(ct), объединить экспоненциальные множители под интегралом и заменить переменную интегрирования w на c+jw:
s(t) = (1/2p)
S(c+jw) exp[(c+jw)t] d(c+jw). (4.2.11)
Обозначим комплексную переменную c+jw в выражениях (4.2.10,4.2.11) через р и получим общепринятую форму прямого и обратного преобразования Лапласа:
S(p) =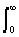s(t) exp[-pt] dt. (4.2.10')
s(t) = (1/2p)S(p) exp(pt) dp. (4.2.11')
Сигнальную функцию s(t) в преобразованиях Лапласа обычно называют оригиналом, а ее спектральную функцию S(p) - изображением оригинала. Пример спектральной функции Лапласа для оригинала - сложного и неограниченного во времени сигнала, состоящего из каузальной суммы трех гармоник, приведен на рис. 4.2.7. По спектральной функции Лапласа можно выделить эти три основных частоты сигнала и оценить соотношение их амплитуд. Ширина пиков спектральной функции при выделении "чистых" гармоник зависит от значения коэффициента 'c' и уменьшается при его уменьшении.
Если вместо р в изображениях оригинала подставить переменную jw, то будут получены спектральные функции, полностью идентичные преобразованию Фурье каузальных функций (имеющих нулевые значения при t<0).
Тригонометрические функции не является единственно возможными функциями разложения сигналов. В общем случае разложение сигнала s(t) на интервале (a, b) в ряд вида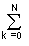 
ckjk(t) может быть выполнено по произвольным функциям jk(t). При задании минимальной погрешности приближения
D
s =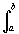
[s(t) - 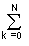ckjk(t)]2 dt
коэффициенты c
k могут быть найдены из системы линейных уравнений:
=
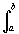
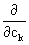[s(t) - 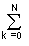ckjk(t)]2 dt = 0, k = 0,1,2,…N.
При линейной независимости функций
jk(t) данная система уравнений имеет единственное решение. Если все функции jk(t) взаимно ортогональны и соответствующей нормировкой обеспечена их ортонормированность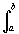jm(t) jn(t) dt =
,
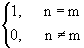то процесс нахождения коэффициентов c
k оказывается наиболее простым:ck =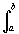s(t) jk(t) dt,
и для принятого значения N погрешность приближения
Ds является минимальной. Если при N ® Ґ имеет место Ds ® 0, система функций jk(t) называется базисной системой координат пространства сигналов L2[a, b] . При этом имеет место равенство:s(t) =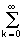
ckjk(t).
Разложение по ортонормированной системе базисных функций называется обобщенным рядом Фурье, а набор коэффициентов c
k представляет собой спектр функции s(t) в соответствующем базисе. В зависимости от специфики решаемых задач применяются различные системы базисных функций. В частности, используются разложения по полиномам Лежандра, Чебышева, Лагерра, Эрмита, функциям Хаара и Уолша и т.п.|
|
 |
