ПРОСТРАНСТВО И МЕТРОЛОГИЯ СИГНАЛОВ
Содержание:
2.1. Пространство сигналов. Линейное пространство сигналов. Норма сигналов. Метрика сигналов. Скалярное произведение сигналов. Коэффициент корреляции сигналов. Координатный базис пространства. 2.2. Мощность и энергия сигналов. Понятия мощности и энергии сигналов. 2.3. Пространства функций. Нормирование метрических параметров. Ортогональные сигналы. Ортонормированный базис пространства. Разложение сигнала в ряд. Ортонормированные системы функций. Разложение энергии сигнала. 2.4. Функции корреляции сигналов. Корреляционные функции сигналов. Взаимная корреляционная функция. 2.5. Математическое описание шумов и помех. Шумы и помехи. Природа помех. Характеристики помех. Литература.ВВЕДЕНИЕ
В данной теме метрология сигналов рассматривается, в основном, на уровне понятий и базовых определений, предваряя их более подробное изучение в дальнейших темах курса. Это объясняется тем, что при детальном изучении каких-либо характеристик или свойств сигналов их рассмотрение не может выполняться в отрыве от других метрологических характеристик рассматриваемых типов сигналов и требует определенной ориентировки в общей метрологии сигналов, хотя бы на уровне понятий
.2.1. Пространство сигналов
Важнейшее свойство аналоговых и дискретных сигналов заключается в том, что их линейные комбинации также являются аналоговыми или дискретными сигналами. Линейные комбинации цифровых сигналов, в силу их ограничения по разрядности, в принципе относятся к разряду нелинейных операций, однако последним фактором можно пренебречь, если ошибки, которые вносятся в результаты наблюдений при квантовании отсчетов, достаточно малы по сравнению с шумами зарегистрированной информации. При дискретизации и квантовании данных непосредственно на входах в ЭВМ последнее выполняется практически всегда, поскольку ошибки определяются разрядностью ЭВМ и программными системами обработки данных, которые обычно не ниже 6-12 десятичных разрядов.
Пространство сигналов.
Пусть L{s1(t), s2(t), …} - множество сигналов, которые имеют какие-то общие свойства и определенную структуру связи между сигналами. Например, множество может состоять из сигналов вида sn(t) = Ancos(wnt+jn)·exp(-at2) – затухающих гармонических колебаний с определенными значениями амплитуд, частот и начальных фаз. Путем введения структурных ограничений множество сигналов может быть превращено в функциональное пространство сигналов. Так, если пространство значений независимой переменной t задано выражением R:=(-Ґ ,+Ґ ), то пространство сигналов Lp[R] определяет множество сигналов в этом пространстве, для которых выполняется условие однозначной реализации: |s(t)|p dt < Ґ .
|s(t)|p dt < Ґ .
Для анализа сигналов наиболее часто используется гильбертово пространство, сигналы в котором должны удовлетворять условию интегрирования с квадратом:
 |s(t)|2 dt < Ґ .
|s(t)|2 dt < Ґ .
Периодические сигналы обычно рассматриваются в пространстве L
2[0,2p] одного периода: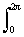 |s(t)|2 dt < Ґ .
|s(t)|2 dt < Ґ .
Линейное пространство сигналов.
Множество сигналов L образует линейное пространство сигналов, если для него справедливы следующие аксиомы:- Для любых сигналов u(t) О L и v(t) О L существует их сумма s(t) = u(t)+v(t), которая также содержится в L. Операция суммирования коммутативна: u(t)+v(t) = v(t)+u(t), и ассоциативна: u(t)+(v(t)+x(t)) = (u(t)+v(t))+x(t).
- Для любого сигнала s(t) О L и числа a определен сигнал y(t) = a s(t), у(t) О L.
- Множество L содержит такой нулевой элемент Ж , что для всех сигналов u(t) О L выполняется равенство u(t)+Ж = u(t).
Пример.
Множество сигналов L состоит из импульсных сигналов произвольной формы с амплитудой не более 10 вольт. Образуют ли эти сигналы линейное пространство?Нет, не образуют, так как не выполняется, по крайней мере, первая аксиома линейного пространства (сумма двух сигналов с амплитудой более 5 вольт превышает 10 вольт). Требуются дополнительные структурные ограничения по параметрам сигналов.
Сигналы могут описываться как вещественными, так и комплексными функциями, и линейные пространства также могут быть вещественными или комплексными.
Множество L, для которого выполняются данные аксиомы, при анализе сигналов и систем может рассматриваться как специальным образом сконструированное многомерное (в пределе – бесконечномерное) геометрическое пространство. Сигналы таких линейных пространств называют векторами
в силу аналогии их свойств со свойствами векторов. Рассмотрим это на конкретном примере.Представим себе произвольный сигнал s(t), заданный на интервале [a, b]. Дискретизируем сигнал с равномерным шагом дискретизации и переведем в цифровую форму (представим N последовательными выборками):
s = (s1, s2, … , sN).
В таком представлении величина s может рассматриваться в виде N-мерного вектора в N-мерном пространстве, в котором значения s
n представляют собой проекции s-вектора на координатные оси данного пространства. Двумерный вектор в двумерном пространстве – это точка с координатами s1 и s2 на рис. 2.1.1. Соответственно, в трехмерном пространстве сигнал s представлен точкой в трехмерном пространстве. Представить себе N-мерное пространство при N>3 можно только абстрактно, но с математических позиций такое пространство вполне реально и N-мерный сигнал s отображается вполне определенной точкой в этом пространстве с координатами sn по осям пространства. При уменьшении интервала дискретизации сигнала до бесконечно малой величины значение N стремится к бесконечности, и пространство сигналов превращается в бесконечномерное пространство аналоговых сигналов. Следовательно, и аналоговые сигналы могут рассматриваться как предельный случай бесконечномерных векторов.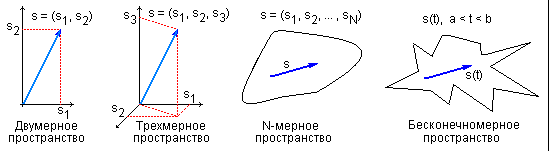
Рис. 2.1.1. Пространства сигналов и функций.
С учетом вышеизложенного, для математического анализа систем и сигналов в линейном пространстве может использоваться математика векторов. Основными метрическими параметрами векторного анализа являются норма, метрика и скалярное произведение сигналов.
Норма сигналов
в линейном пространстве является аналогом длины векторов и обозначается индексом ||s(t)|| - норма (norm). В математике существуют различные формы норм. При анализе сигналов обычно используются квадратичные нормы:||s(t)|| =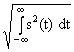 . (2.1.2)
. (2.1.2)
Соответственно, для дискретных сигналов:
||s(t)|| =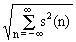 . (2.1.2')
. (2.1.2')
Для комплексных сигналов
:||s(t)|| =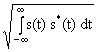 , (2.1.2'')
, (2.1.2'')
где s*(t) – величины, комплексно сопряженные с s(t).
Линейное пространство сигналов L является нормированным, если каждому сигналу пространства s(t) однозначно сопоставлена его числовая норма ||s(t)||, и выполняются следующие аксиомы:
- Норма неотрицательна и равна нулю тогда и только тогда, когда сигнал равен нулю (||s(t)|| =
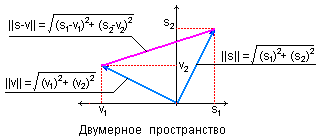
Пример норм для двумерных цифровых сигналов приведен на рис. 2.1.2.
Метрика сигналов.
Линейное пространство сигналов L является метрическим, если каждой паре сигналов s(t) О L и v(t) О L однозначно сопоставляется неотрицательное число r (s(t),v(t)) – метрика (metric) или расстояние между векторами. Пример метрики для двух векторов в двумерном пространстве приведен на рис. 2.1.2.Для метрик сигналов в метрическом пространстве любой размерности должны выполняться аксиомы:
- r (s(t),v(t)) = r (v(t),s(t)) – рефлексивность метрики.
- r (s(t),s(t)) = 0 для любых s(t) О L.
- r (s(t),v(t)) Ј r (s(t),a) + r (a,v(t)) для любых a О L.
Метрика определяется нормой разности двух сигналов (см. рис. 2.1.2)
:r
(s(t),v(t)) = || s(t) – v(t) ||. (2.1.3)В свою очередь норму можно отождествлять с расстоянием от выбранного элемента пространства до нулевого
: ||s(t)|| = r (s(t),Ж ).По метрике сигналов можно судить, например, о том, насколько точно один сигнал может быть аппроксимирован другим сигналом, или насколько изменяется выходной сигнал относительно входного при прохождении через какое-либо устройство.
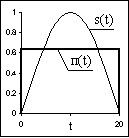
Пример.
Сигнал на интервале (0,Т) представляет собой половину периода синусоиды амплитудой A: s(t) = AЧ sin(p t/T), 0 Ј t Ј T. Требуется аппроксимировать сигнал прямоугольным импульсом п(t) (см. рис. 2.1.3).Если принять амплитуду импульса п(t) равной В, то квадрат расстояния между сигналами:
r 2(s,п) =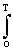 (A sin(p t/T)-В)2 dt = A2T/2 - 4ABT/p + B2T.
(A sin(p t/T)-В)2 dt = A2T/2 - 4ABT/p + B2T.
Для решения задачи требуется найти минимум выражения
r 2(s,п). Дифференцируем полученное выражение по В, приравниваем нулю и, решая относительно В, находим значение экстремума: В = 2A/p » 0.64А. Это искомое значение минимума функции r 2(s,п), так как вторая производная функции по В положительна. При этом минимальное значение метрики: r min » 0.31A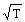 . Вычислим нормы сигналов при А = 1:
. Вычислим нормы сигналов при А = 1:
Е
s = А2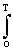 sin2 (p t/T) dt = A2 T/2 = 10. Норма: ||s(t)|| =
sin2 (p t/T) dt = A2 T/2 = 10. Норма: ||s(t)|| =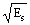 = 0.707 A
= 0.707 A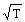 » 3.16.
» 3.16.
Еп
= B2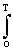 dt = B2 T » 8.1. Норма: ||п(t)|| =
dt = B2 T » 8.1. Норма: ||п(t)|| = 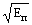 = B
= B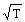 » 2.85.
» 2.85.
Скалярное произведение произвольных сигналов
u(t) и v(t) отражает степень их связи (сходства) по форме и положению в пространстве сигналов, и обозначается как б u(t), v(t)с .б
u(t), v(t)с = ||u(t)||Ч ||v(t)|| cos j , (2.1.4)Физическую сущность скалярного произведения векторов в двумерном пространстве можно видеть достаточно наглядно (рис. 2.1.4). Это произведение "длины" (нормы) одного вектора на проекцию второго вектора по "направлению" первого вектора.
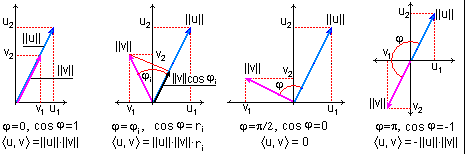
Рис. 2.1.4. Скалярное произведение сигналов в двумерном пространстве.
При кажущейся абстрактности скалярного произведения сигналов оно может приобретать вполне конкретный физический смысл для конкретных физических процессов, которые отображаются этими сигналами. Так, например, если v = F – сила, приложенная к телу, а u = s – перемещение тела под действием этой силы, то скалярное произведение W = F·s определяет выполненную работу, при условии совпадения силы с направлением перемещения. В противном случае, при наличии угла
j между векторами силы и перемещения, работа будет определяться проекцией силы в направлении перемещения, т.е. W = s·F·cos j.Вычисление скалярного произведения обычно производится непосредственно по сигнальным функциям. Поясним это на примере двумерных сигналов с использованием рисунка 2.1.2. Для квадрата метрики сигналов s и v имеем:
||s-v||2 = ||s||2 + ||v||2 – 2 ||s|| ||v|| cos j = ||s||2 + ||v||2 – 2 б s, vс .
2 б s,vс = ||s||2 + ||v||2 - ||s-v||2 = (s12+s22)+(v12+v22)–{(s1-v1)2+(s2-v2)2} = 2 (s1v1+s2v2).
б
s,vс = s1v1+s2v2.Обобщая полученное выражение на аналоговые сигналы:
б
s(t), v(t)с =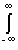 s(t)v(t) dt. (2.1.5)
s(t)v(t) dt. (2.1.5)
Соответственно, для дискретных сигналов в N-мерном пространстве:
б
sn, vnс =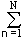 sn vn. (2.1.5')
sn vn. (2.1.5')
Скалярное произведение обладает следующими свойствами
:- б s,vс і 0;
- б s,vс = б v,sс ;
- б as,vс = aб s,vс , где а – вещественное число;
- б s+v, aс = б s,aс + б v,aс .
Линейное пространство аналоговых сигналов с таким скалярным произведением называется гильбертовым пространством Н (второе распространенное обозначение - L
2). Линейное пространство дискретных и цифровых сигналов - пространством Евклида (обозначение пространства - R2). В этих пространствах справедливо фундаментальное неравенство Коши-Буняковского (модуль косинуса в (2.1.4) может быть только равным или меньше 1):|б s,vс | Ј ||s||Ч ||v||. (2.1.6)
Для комплексного гильбертова пространства скалярное произведение вычисляется по формуле
:б
s(t), v(t)с =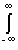 s(t)v*(t) dt. (2.1.7)
s(t)v*(t) dt. (2.1.7)При определении функций в пространстве L
2[a,b] вычисление скалярного произведения производится соответственно с пределами интегрирования от а до b.Из выражения (2.1.4) следует косинус угла между сигналами:
cos j = б s(t),v(t)с /(||s||Ч ||v||). (2.1.8)
Пример.
Имеется два смещенных во времени прямоугольных импульса с одинаковой амплитудой и длительностью: s1(t) = 2 при 0 Ј t Ј 5, s1(t) = 0 при других t; и s2(t) = 2 при 4 Ј t Ј 9, s2(t) = 0 при других t.Квадраты норм сигналов: ||s
1||2 =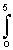 s12(t)dt = 20. ||s2||2 =
s12(t)dt = 20. ||s2||2 =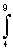 s22(t)dt = 20
s22(t)dt = 20
Скалярное произведение:
б s1,s2с =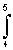 s1(t) s2(t) dt = 8.
s1(t) s2(t) dt = 8.
Отсюда имеем: cos
j = (s1,s2)/ (||s1||Ч ||s2||) = 8/20 = 0.4 и j » 1.16 радиан » 66оПри полном совмещении сигналов:
б s1,s2с =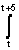 s1(t) s2(t) dt = 20, cos j = 1, j = 0.
s1(t) s2(t) dt = 20, cos j = 1, j = 0.
При отсутствии перекрытия сигналов;
б s1,s2с = 0, cos j = 0, j = 90о.Физическое понятие "угла" между многомерными сигналами довольно абстрактно. Однако при рассмотрении выражения (2.1.8) совместно с выражением для квадрата метрики сигналов
r2
(s,v) =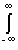 [s(t)-v(t)]2 dt = ||s||2 + ||v||2 - 2Ч ||s||Ч ||v|| cos j .
[s(t)-v(t)]2 dt = ||s||2 + ||v||2 - 2Ч ||s||Ч ||v|| cos j .
можно отметить следующие закономерности. При
j = 0 (cos j = 1) сигналы "совпадают по направлению" и расстояние между ними минимально. При j = p/2 (cos j = 0) сигналы "перпендикулярны друг другу" (иначе говоря – ортогональны), и проекции сигналов друг на друга равны 0. При j = p (cos j = -1) сигналы "противоположны по направлению" и расстояние между сигналами максимально. Фактор расстояния между сигналами играет существенную роль при их селекции в многоканальных системах.Коэффициент корреляции сигналов.
Одновременно заметим, что значение косинуса в (2.1.8) изменяется от 1 до -1, и не зависит от нормы сигналов ("длины" векторов). Максимальное значение cos j = 1 соответствует полной тождественности относительной динамики сигналов, минимальное значение cos j = -1 наблюдается при полной противоположности значений относительной динамики сигналов. По существу, коэффициент r = cos j является интегральным коэффициентом степени сходства формы сигналов по пространству их задания. С учетом этого он и получил название коэффициента корреляции сигналов. На рис. 2.1.5 можно наглядно видеть значения коэффициента корреляции двух сигналов в зависимости от их формы и сдвига по независимой переменной.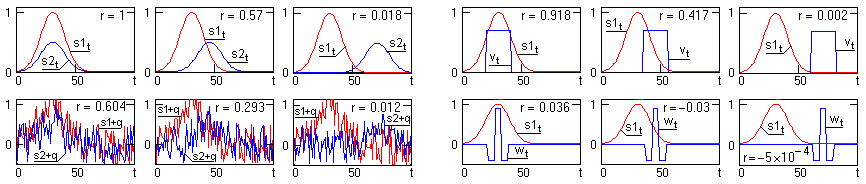
Рис. 2.1.5. Коэффициент корреляции сигналов.
Однако количественные значения коэффициентов корреляции существенно зависят от выбора нулевой точки сигнального пространства. Рассмотрим это более детально на конкретном примере.
На рис. 2.1.6 приведено изменение средней месячной температуры воздуха в трех городах земного шара в течение одного календарного года. Характер корреляции между изменениями температур в городах достаточно хорошо виден на графиках. Вычислим (см. пример ниже) значения коэффициентов корреляции для шкалы температур по Цельсию.
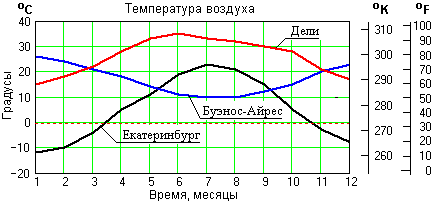
Рис. 2.4.1.
Пример.
Среднемесячная температура воздуха в городах по Цельсию:Екатеринбург: Ek = {-12,-10,-4,5,11,19,23,21,15,5,-3,-8}. Дели: Dk = {15,18,22,28,33,35,33,32,30,28,21,17}.
Буэнос - Айрес: B
k = {26,24,21,18,14,11,10,10,12,15,20,23}. Нумерация месяцев: k = 1, 2, 3, …, 12.Норма сигналов: ||E|| = 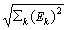
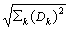 = 93.05, ||B|| =
= 93.05, ||B|| = 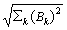 = 61.9.
= 61.9.
Скалярные произведения:
б E, Dс =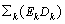 = 2542, б E, Bс = 268, б B, Dс = 4876.
= 2542, б E, Bс = 268, б B, Dс = 4876.
Коэффициенты корреляции: Екатеринбург – Дели:
rED = б E, Dс / (||E|| ||D||) = 0.602.Екатеринбург – Буэнос-Айрес:
rEB = 0.095, Дели – Буэнос-Айрес: rDB = 0.847,Как следует из вычислений, полученные коэффициенты корреляции маловыразительны. Практически не регистрируется разнонаправленная корреляция Екатеринбург - Буэнос-Айрос, и не различаются одно- (Екатеринбург – Дели) и разнонаправленные (Дели – Буэнос-Айрос) типы корреляции.
Повторим вычисления в шкале Фаренгейта (0о
F = -17,8oC, 100oF = +37,8oC), и в абсолютной шкале температур Кельвина. Дополнительно вычислим значения коэффициентов корреляции в шкале Цельсия и Фаренгейта для центрированных сигналов. Центрированный сигнал вычисляется путем определения среднего значения сигнала по интервалу его задания и вычитания этого среднего значения из исходных значений сигнала, т.е. среднее значение центрированного сигнала равно нулю. Сводные результаты вычислений приведены в таблице.Таблица 2.1.1.
Коэффициенты корреляции сигналов
|
Пары городов |
Нецентрированные сигналы |
Центрированные сигналы |
|||
|
Цельсий |
Фаренгейт |
Кельвин |
Цельсий |
Фаренгейт |
|
|
Екатеринбург – Дели Екатеринбург – Буэнос-Айрес Дели – Буэнос-Айрес |
0.602 0.095 0.847 |
0.943 0.803 0.953 |
1 0.998 0.999 |
0.954 -0.988 -0.960 |
0.954 -0.988 -0.960 |
Как видно из таблицы, значения коэффициента корреляции нецентрированных сигналов существенно зависят от положения сигналов относительно нулевой точки пространства. При одностороннем смещении сигналов относительно нуля (шкала Фаренгейта) значение коэффициента корреляции может быть только положительным, и тем ближе к 1, чем дальше от сигналов нулевая точка (шкала Кельвина), т.к. при больших значениях сигналов-векторов значение скалярного произведения сигналов стремится к значению произведения норм сигналов.
Для получения значений коэффициентов корреляции, независимых от нуля сигнального пространства и от масштаба единиц измерений, необходимо вычислять коэффициент по центрированным сигналам, при этом в оценках коэффициента, как это видно из результатов, приведенных в таблице, появляется знаковый параметр совпадения (или несовпадения) по "направлению" корреляции и исчезает зависимость от масштаба представления сигналов. Это позволяет вычислять коэффициенты корреляции различных сигналов вне зависимости от физической природы сигналов и их величины.
Координатный базис пространства.
Для измерения и отображения одномерных величин достаточно одного нормированного параметра – стандарта величины или единицы ее измерения (для измерения длины – сантиметр, для измерения тока – ампер, и т.п.).В пространстве сигналов роль такого метрологического стандарта выполняет координатный базис пространства - подмножество векторов {е
1, е2, е3, …} со свойствами ортогональных координатных осей, по которым можно разложить любой произвольный сигнал, принадлежащий этому линейному пространству.Совокупность векторов e
i пространства L является линейно независимой и образует координатный базис пространства, если равенство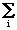 aiei = Ж выполняется только в случае одновременного обращения в нуль всех числовых коэффициентов ai. При этом произвольный сигнал s(t) может быть разложен по координатному базису ei в виде
aiei = Ж выполняется только в случае одновременного обращения в нуль всех числовых коэффициентов ai. При этом произвольный сигнал s(t) может быть разложен по координатному базису ei в видеs(t) =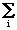 сiei, (2.1.9)
сiei, (2.1.9)
где числа с
i – проекции сигнала s(t) на координатный базис.Число базисных векторов определяет размерность векторного пространства. Так, для двумерных векторов в качестве ортогонального базиса пространства могут быть приняты векторы {v
1, v2}, если выполняется условие их взаимной перпендикулярности – нулевое значение скалярного произведения б v1, v2с = 0. При ||v1|| = ||v2|| = 1 эта пара векторов является ортонормированным базисом с единичными векторами координатных осей в качестве стандарта (единицы измерения) пространства.Пример.
Могут ли быть приняты в качестве координатного базиса двумерного пространства векторыv1 = (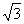 /2, 1/2), v2 = (-1/2,
/2, 1/2), v2 = (-1/2, 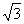 /2).
/2).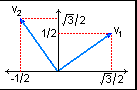
б
v1, v2с = (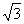 /2)·(-1/2) + (1/2)·(
/2)·(-1/2) + (1/2)·(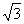 /2) = 0. Векторы ортогональны.
/2) = 0. Векторы ортогональны.
||v1|| = 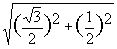 = 1.
= 1.
||v2|| = 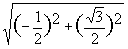 = 1. Векторы нормированы.
= 1. Векторы нормированы.
Векторы могут быть ортонормированным базисом пространства.
Разложение произвольного двумерного вектора - сигнала s в двумерном пространстве по координатным осям элементарно:
s = c1v1 + c2v2, (2.1.10)
где коэффициенты с
1 и с2 выражают значения составляющих вектора s по направлениям векторов v1 и v2, т.е. являются проекциями вектора s на координатный базис пространства {v1, v2}. Значения проекций определяются скалярными произведениями:c1 = б s, v1с , c2 = б s, v2с .
В последнем нетрудно убедиться, если вычислить скалярные произведения левой и правой части выражения (2.1.10) сначала с вектором v
1:б
s, v1с = б (c1v1+c2v2), v1с = б с1v1, v1с + б с2v2, v1с = с1б v1, v1с + с2б v2, v1с .При ортонормированности базиса {v
1, v2} имеем:б
v1, v1с = ||v1||2 = 1, б v2, v1с = 0.Отсюда следует:
б s, v1с = с1. Аналогичным образом можно получить и выражение для значения c2 = б s, v2с .Пример.
Разложить вектор s = (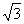 /2, 5/2) по базису, представленному векторами
/2, 5/2) по базису, представленному векторами
v1 = (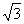 /2, 1/2) и v2 = (-1/2,
/2, 1/2) и v2 = (-1/2, 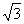 /2) из предыдущего примера.
/2) из предыдущего примера.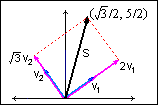
s = c1v1 + c2v2.
с
1 = б s, v1с = (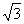 /2)·(
/2)·(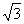 /2) + (5/2)·(1/2) = 2.
/2) + (5/2)·(1/2) = 2.
с
2 = б s, v2с = (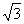 /2)·(-1/2) + (5/2)·(
/2)·(-1/2) + (5/2)·(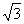 /2) =
/2) = 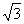 .
.
Результат:
В пространстве с базисом {v1, v2} вектор s однозначно определяется двумя векторами v1 и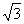 векторами v2. s = 2v1 +
векторами v2. s = 2v1 + 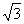 v2.
v2.
2.2. Мощность и энергия сигналов [1,3,16].
Понятия мощности и энергии
в теории сигналов не относятся к характеристикам каких-либо физических величин сигналов, а являются их количественными характеристиками, отражающими определенные свойства сигналов и динамику изменения их значений (отсчетов) во времени, в пространстве или по любым другим аргументам.Для произвольного, в общем случае комплексного, сигнала s(t) = a(t)+jb(t), где а(t) и b(t) - вещественные функции, мгновенная мощность (instantaneous power) сигнала по определению задается выражением:
w(t) = s(t) s*(t) = [a(t)+jb(t)] [a(t)-jb(t)] = a2(t)+b2(t) = |s(t)|2, (2.2.1)
т.е. функция распределения мгновенной мощности по аргументу сигнала равна квадрату функции его модуля, для вещественных сигналов - квадрату функции амплитуд.
Аналогично для дискретных сигналов:
wn = sn s*n = [an+jbn] [an-jbn] = an2 + bn2 = |sn|2, (2.2.1')
Энергия сигнала (также по определению) равна интегралу от мощности по всему интервалу существования или задания сигнала. В пределе:
Е
s =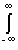 w(t)dt =
w(t)dt =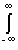 |s(t)|2dt. (2.2.2)
|s(t)|2dt. (2.2.2)Es =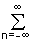 wn =
wn =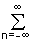 |sn|2. (2.2.2')
|sn|2. (2.2.2')
Мгновенная мощность w(t) является плотностью мощности сигнала, так как измерения мощности возможны только через энергию на интервалах ненулевой длины:
w(t) = (1/Dt)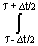 |s(t)|2dt.
|s(t)|2dt.
Энергия сигналов может быть конечной или бесконечной. Конечную энергию имеют финитные сигналы и сигналы, затухающие по своим значениям в пределах конечной длительности, которые не содержат дельта-функций и особых точек (разрывов второго рода и ветвей, уходящих в бесконечность). В противном случае их энергия равна бесконечности. Бесконечна также энергия периодических сигналов.
Как правило, сигналы изучаются на определенном интервале Т, для периодических сигналов - в пределах одного периода Т, при этом средняя мощность (average power) сигнала:
WT(t) = (1/T)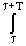 w(t) dt = (1/T)
w(t) dt = (1/T)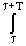 |s(t)|2 dt. (2.2.3)
|s(t)|2 dt. (2.2.3)
Понятие средней мощности может быть распространено и на незатухающие сигналы, энергия которых бесконечно велика. В случае неограниченного интервала Т строго корректное определение средней мощности сигнала должно производиться по формуле:
Ws = 
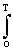 w(t) dt. (2.2.3')
w(t) dt. (2.2.3')
Квадратный корень из значения средней мощности характеризует действующее (среднеквадратическое) значение сигнала (root mean sqare, RMS).
Применительно к электрофизическим системам, данным понятиям мощности и энергии соответствуют вполне конкретные физические величины. Допустим, что функцией s(t) отображается электрическое напряжение на резисторе, сопротивление которого равно R Ом. Тогда рассеиваемая в резисторе мощность, как известно, равна (в вольт-амперах):
w(t) = |s(t)|2/R,
а полная выделенная на резисторе тепловая энергия определяется соответствующим интегрированием мгновенной мощности w(t) по интервалу задания напряжения s(t) на резисторе R. Физическая размерность мощности и энергии в этом случае определяется соответствующей физической размерностью функции напряжения s(t) и сопротивления резистора R. Для безразмерной величины s(t) при R=1 это полностью соответствует выражению (2.2.1). В теории сигналов в общем случае сигнальные функции s(t) не имеют физической размерности, и могут быть формализованным отображением любого процесса или распределения какой-либо физической величины, при этом понятия энергии и мощности сигналов используются в более широком смысле, чем в физике. Они представляют собой специфические метрологические характеристики сигналов.
Из сравнения выражений (2.1.2) и (2.2.2) следует, что энергия и норма сигнала связаны соотношениями:
Es = ||s(t)||2, ||s(t)|| =  (2.2.4)
(2.2.4)
Пример.
Цифровой сигнал задан функцией s(n) = {0,1,2,3,4,5,4,3,2,1,0,0,0,0....}.Энергия сигнала: Es = 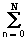 s2(n) = 1+4+9+16+25+16+9+4+1 = 85. Норма: ||s(n)|| =
s2(n) = 1+4+9+16+25+16+9+4+1 = 85. Норма: ||s(n)|| = 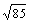 » 9.22
» 9.22
Вычислим энергию суммы двух произвольных сигналов u(t) и v(t)
:E =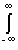 [u(t)+v(t)]2 dt = Eu + Ev + 2
[u(t)+v(t)]2 dt = Eu + Ev + 2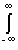 u(t)v(t) dt. (2.2.5)
u(t)v(t) dt. (2.2.5)
Как следует из этого выражения, энергии сигналов (а равно и их мощности), в отличие от самих сигналов, в общем случае не обладают свойством аддитивности. Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию
:Euv = 2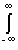 u(t)v(t) dt. (2.2.6)
u(t)v(t) dt. (2.2.6)
Нетрудно заметить, что энергия взаимодействия сигналов равна их удвоенному скалярному произведению
:Euv = 2 б u(t), v(t)с . (2.2.6')
При обработке данных используются также понятия мощности взаимодействия двух сигналов x(t) и y(t):
wxy(t) = x(t) y*(t), (2.2.7)
wyx(t) = y(t) x*(t),
wxy(t) = w*yx(t).
Для вещественных сигналов:
wxy(t) = wyx(t) = x(t) y(t). (2.2.8)
С использованием выражений (2.2.7-8) интегрированием по соответствующим интервалам вычисляются значения средней мощности взаимодействия сигналов на определенных интервалах Т и энергия взаимодействия сигналов.
2.3. пространства функций [1,3,11,16,29].
Пространства функций можно считать обобщением пространства N-мерных сигналов – векторов на аналоговые сигналы, как бесконечномерные векторы, с некоторыми чисто практическими уточнениями.
Нормирование метрических параметров. Норма функций в пространстве L2[a, b] определяется выражением:
||s(t)|| =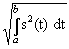 .
.
Нетрудно заключить, что чем больше интервал [a, b] в этой формуле, тем больше (при прочих равных условиях) будет значение нормы. При анализе и сравнении сигналов (как аналоговых, так и многомерных дискретных) такое понятие не всегда удобно, и вместо него очень часто используют понятие нормы, нормированной относительно длины интервала[a, b]. Для символьного обозначения нормирования будем применять знак
С :||s(t)||С =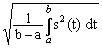 , ||sn||С =
, ||sn||С =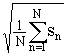 .
.
Метрика сигналов (расстояние между сигналами) при аналогичном нормировании:
dС (s(t), v(t)) =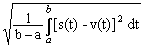 , dС (sn, vn) =
, dС (sn, vn) = 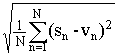
Эти выражения применяются для вычисления среднеквадратического расхождения сигналов или среднеквадратической погрешности выполнения какой-либо операции при сравнении ее результата с теоретически ожидаемым или априорно известным.
Нормированное скалярное произведение сигналов:
б
s(t), v(t)с С = s(t)v(t) dt = ||s(t)||С ||v(t)||С cos j.
s(t)v(t) dt = ||s(t)||С ||v(t)||С cos j.
б
sn, vnс С =(1/N)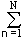 sn vn = ||sn||С ||sn||С cos j.
sn vn = ||sn||С ||sn||С cos j.
Косинус угла (коэффициент корреляции) между сигналами – функциями не изменяет своих значений при вычислении как по нормированным, так и по ненормированным значениям скалярного произведения и нормы сигналов (значения нормировки в числителе и знаменателе выражения (2.1.8) сокращаются). Взаимная перпендикулярность функций определяется аналогично взаимной перпендикулярности векторов условием нулевого значения скалярного произведения.
Норма, метрика и скалярное произведение периодических функций обычно нормируются на длину главного периода Т.
Ортогональные сигналы.
Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение:б
u(t), v(t)с = u(t)v(t) dt = 0.
u(t)v(t) dt = 0.
Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными (угол между сигналами равен
j = 90о), полностью независимыми друг от друга (некоррелированными, r = cos j = 0), и имеют нулевую энергию взаимодействия (Euv = 0).На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевое скалярное произведение двух левых сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух правых - взаимным расположением (ненулевые значения сигналов не имеют общих координат).
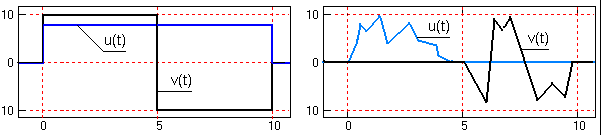
Рис. 2.3.1. Ортогональные сигналы.
Попутно заметим, что энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности, т.к. имеют нулевое значение скалярного произведения и, соответственно, энергии взаимодействия.
Ортонормированный базис пространства.
Множество сигналов – векторов {vk, k = 1, 2, …, N} в N-мерном декартовом пространстве при единичной норме и выполнении условий взаимной ортогональности:б
vm, vnс =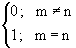 (2.3.1)
(2.3.1)
могут быть приняты в качестве ортонормированного базиса данного пространства. Выражение (2.3.1) обычно записывается в следующей форме:
б
vm, vnс = dmn, (2.3.1')где
dmn – импульс Кронекера, равный правой части выражения (2.3.1).С использованием ортонормированного базиса любой произвольный сигнал можно представить в виде линейной комбинации взвешенных базисных векторов:
s = c1v1 + c2v2 + … + cNvN,
где весовое значение с
k определяется проекцией вектора s на соответствующее координатное направление:ck = б s, vkс .
При распространении данных положений на функциональное пространство L
2[a, b] в качестве координатного базиса пространства мы должны использовать совокупность функций {u0(t), u1(t), u2(t), …}, в пределе - бесконечную, которая должна быть системой ортогональных функций {uk(t), k=0, 1, 2, …}, т.е. все функции на этом отрезке должны быть взаимно ортогональны:б
um(t), un(t)с = um(t) un(t) dt = 0, m = 1, 2, ... ; n = 1, 2, ... ; m № n.
um(t) un(t) dt = 0, m = 1, 2, ... ; n = 1, 2, ... ; m № n.
Система ортогональных функций на интервале [a, b] будет ортонормированной (orthonormal functions), если все функции системы при m=n имеют единичную норму, т.е. выполняются условия:
б
um(t), um(t)с = ||um(t)||2 = (um(t))2 dt = 1, ||um(t)|| = 1, m = 1, 2, ....
(um(t))2 dt = 1, ||um(t)|| = 1, m = 1, 2, ....
Эти условия можно записать в следующей обобщенной форме:
 um(t)·un*(t) dt = dm,n.
um(t)·un*(t) dt = dm,n.
Система ортогональных функций всегда может быть превращена в ортонормированную путем нормировки, т.е. деления всех функций на их норму.
Разложение сигнала в ряд.
Произвольный сигнал s(t) О H (пространство Гильберта), заданный на интервале [a, b], может быть разложен в ряд по упорядоченной системе ортонормированных базисных функций uk(t):s(t) =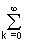 ckuk(t). (2.3.2)
ckuk(t). (2.3.2)
Для нахождения значений коэффициентов с
k умножим обе части данного выражения на базисную функцию um(t) с произвольным номером m и проинтегрируем результаты по переменной t, при этом получим: s(t)um(t) dt =
s(t)um(t) dt =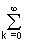 ck
ck  umuk dt.
umuk dt.
С учетом ортонормированности функций u
i(t), в правой части этого равенства остается только один член суммы с номером m = k при ukuk dt =1, который, по левой части уравнения, представляет собой скалярное произведение сигнала и соответствующего m = k базисного вектора, т.е. проекцию сигнала на соответствующее базисное направление:
ukuk dt =1, который, по левой части уравнения, представляет собой скалярное произведение сигнала и соответствующего m = k базисного вектора, т.е. проекцию сигнала на соответствующее базисное направление: ck = s(t)uk(t) dt. (2.3.2)
s(t)uk(t) dt. (2.3.2)
Таким образом, в геометрической интерпретации коэффициенты с
k представляют собой проекции вектор - сигнала s(t) на соответствующие базисные направления uk(t), т.е. координаты вектора s(t) по координатному базису, образованному системой ортогональных функций u(t), в пределе - бесконечномерной. При практическом использовании количество членов ряда (2.3.2) ограничивается определенным значением N, при этом для любого значения N совокупность коэффициентов ck обеспечивают наименьшее по средней квадратической погрешности приближение к заданному сигналу.Соответственно, энергия взаимодействия двух сигналов x(t) и y(t) может вычисляться по скалярному произведению их координатных проекций, которое, с учетом взаимной ортогональности всех проекций, будет равно:
б
x(t), y(t)с = x(t)y(t) dt =
x(t)y(t) dt = [
[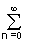 anun(t)] [
anun(t)] [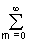 bmum(t)] dt =
bmum(t)] dt =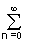 anЧ bn. (2.3.3)
anЧ bn. (2.3.3)
Косинус угла между векторами x(t) и y(t) с использованием выражения (2.3.3):
cos j =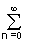 anЧ bn /(||x(t)||Ч ||y(t)||).
anЧ bn /(||x(t)||Ч ||y(t)||).
Возможность разложения непрерывных сигналов и функций в обобщенные ряды по системам ортогональных функций имеет огромное принципиальное значение, так как позволяет вместо изучения несчетного множества точек сигнала ограничиться счетной системой коэффициентов ряда.
К системам базисных функций, которые используются при разложении сигналов, предъявляют следующие основные требования:
- для любого сигнала ряды разложения должны сходиться;
- при ограничении ряда по уровню остаточной погрешности расхождения с заданным сигналом количество членов ряда должно быть минимальным;
- функции должны иметь достаточно простую аналитическую форму;
- коэффициенты разложения должны вычисляться относительно просто.
Согласно теореме Дирехле, любой сигнал s(t), имеющий конечное число точек нарушения непрерывности первого рода и конечный по энергии на интервале [a, b], может быть разложен по системе ортонормальных функций, если существуют интегралы модуля сигнала и модуля его первой производной, т.е.:
 |s(t)| dt < Ґ ,
|s(t)| dt < Ґ ,  |s'(t)| dt < Ґ .
|s'(t)| dt < Ґ .
Ортонормированные системы функций
хорошо известны в математике. Это полиномы Эрмита, Лежандра, Чебышева, функции Бесселя, Лагерра и целый ряд других. Выбор типа функций в качестве координатного базиса сигнального пространства, как и координатных осей для обычного трехмерного пространства (декартовы, цилиндрические, сферические и пр.), определяется удобством и простотой последующего использования при математической обработке сигналов. При спектральном анализе сигналов используются, в основном, два вида ортонормированных функций: гармонические функции и функции Уолша.На интервале [-
p, p] рассмотрим систему следующих гармонических функций:{1, sin t, sin 2t, …, sin kt}, k = 1, 2, 3, … (2.3.4)
Вычислим нормированные на интервал скалярные произведения системы:
б
1, sin ktс =(1/2p)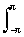 sin kt dt = (1/2kp) [cos kp - cos(-kp)] = 0, k = 1, 2, 3, …
sin kt dt = (1/2kp) [cos kp - cos(-kp)] = 0, k = 1, 2, 3, …
б
sin mt, sin ntс =(1/2p)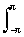 sin mt sin nt dt =(1/4p)
sin mt sin nt dt =(1/4p)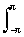 {cos (m+n)t – cos (m-n)t} dt =
{cos (m+n)t – cos (m-n)t} dt =
= 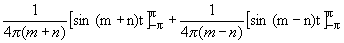 = 0, при m № n.
= 0, при m № n.
Следовательно, система (2.3.4) является системой взаимно ортогональных функций. Норма функций:
||sin kt||2=(1/2p)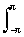 sin2 kt dt= (1/4p)
sin2 kt dt= (1/4p)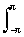 (1-cos 2kt) dt=
(1-cos 2kt) dt=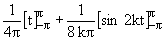 =1/2.
=1/2.
||sin kt|| = 1/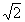 , k = 1, 2, 3, …
, k = 1, 2, 3, …
Соответственно, для превращения системы (2.3.4) в ортонормированную следует разделить все функции системы на значение нормы (рис. 2.3.2):
{1, uk(t) =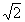 sin kt}, k = 1, 2, 3, … (2.3.4')
sin kt}, k = 1, 2, 3, … (2.3.4')
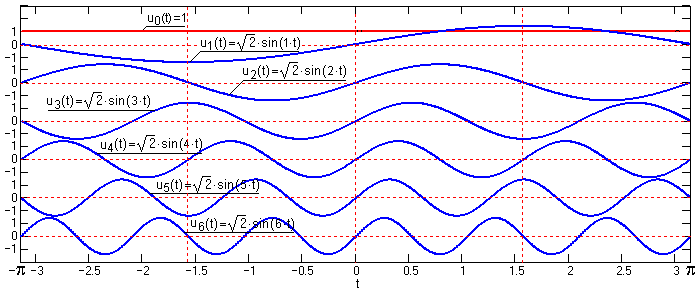
Рис. 2.3.2. Ортонормированный базис гармонических функций.
Аналогичным образом можно убедиться в ортонормированности косинусной системы гармонических функций:
{1, uk(t) =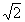 cos kt}, k = 1, 2, 3, …, (2.3.5)
cos kt}, k = 1, 2, 3, …, (2.3.5)
и объединенной синус-косинусной системы:
{1, uk(t) =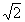 sin kt, uk(t) =
sin kt, uk(t) =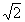 cos kt}, k = 1, 2, 3, … (2.3.6)
cos kt}, k = 1, 2, 3, … (2.3.6)
Наибольшее распространение в качестве базисных функций частотного разложения нашли комплексные экспоненциальные функции exp(pt) при p = jf (преобразование Фурье) и p = s+jf (преобразование Лапласа), от которых с использованием формул Эйлера
exp(jwt) = cos(wt) + j sin(wt), exp(-jwt) = cos(wt) - j sin(wt),
cos(wt) = [ехр(jwt)+exp(-jwt)]/2, sin(wt) = [ехр(jwt)-exp(-jwt)]/2j
всегда можно перейти к синус-косинусным функциям. Термин "частотного" обязан своим происхождением независимой переменной частотного представления сигналов, которая измеряется в единицах, обратных единицам времени, т.е. в единицах частоты f = 1/|t|. Однако понятие частотного преобразования не следует связывать только с временным представлением сигналов, т.к. математический аппарат преобразования не зависит от физического смысла переменных. Так, например, при переменной "х", как единице длины, значение f будет представлять собой пространственную частоту - число периодических изменений сигнала на единице длины с размерностью 1/|х|.
Ортонормированная система функций Уолша, по существу, является предельной модификацией системы периодических функций с кратными частотами, при этом функции принимают значения только
± 1. Пример четырех первых функций Уолша на интервале Т от –0,5 до 0,5 приведен на рис. 2.3.3. Ортогональность и нормированность функций следует из принципа их построения. Стандартное математическое обозначение функций Уолша: wal(k,х), где k = 0,1,2, … – порядковый номер функции, х = t/T – безразмерная координата (нормированная на интервал Т независимая переменная).Наряду с функциями Уолша применяются также две связанные с ними системы
: четные и нечетные функции cal(n,х) = wal(2n,х), – аналогичные косинусам, и sal(n,х) = wal (2n-1,х), – аналогичные синусам.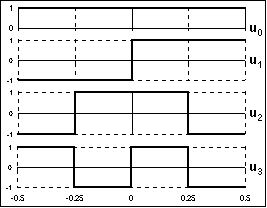
Рис. 2.3.3. Функции Уолша.
При разложении сигналов форма спектров Уолша практически тождественна спектрам гармонических функций.
Разложение энергии сигнала.
Допустим, что сигнал s(t) разложен в обобщенный ряд Фурье (2.3.2). Вычислим энергию сигнала непосредственной подстановкой выражения (2.3.2) в выражение (2.2.2):Es =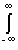 s2(t) dt =
s2(t) dt =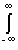
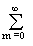
 cmcnumun dt =
cmcnumun dt =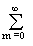
 cmcn
cmcn 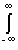 umun dt. (2.3.7)
umun dt. (2.3.7)
В этом выражении в силу ортонормированности базисной системы отличны от нуля только члены с номерами m = n. Отсюда
:Es =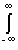 s2(t) dt =
s2(t) dt = cn2, (2.3.8)
cn2, (2.3.8)
т.е. при корректном разложении сигнала в обобщенный ряд Фурье энергия сигнала не изменяется, и равна сумме энергии всех составляющих ряда. Это соотношение называют равенством Парсеваля.
2.4. Функции корреляции сигналов [1, 25, 29].
Функции корреляции сигналов применяются для интегральных количественных оценок формы сигналов и степени их сходства друг с другом.
Автокорреляционные функции (АКФ) сигналов
(correlation function, CF). Применительно к детерминированным сигналам с конечной энергией АКФ является количественной интегральной характеристикой формы сигнала, и представляет собой интеграл от произведения двух копий сигнала s(t), сдвинутых относительно друг друга на время t:Bs(t) =  s(t) s(t+t) dt. (2.4.1)
s(t) s(t+t) dt. (2.4.1)
Как следует из этого выражения, АКФ является скалярным произведением сигнала и его копии в функциональной зависимости от переменной величины значения сдвига
t. Соответственно, АКФ имеет физическую размерность энергии, а при t = 0 значение АКФ непосредственно равно энергии сигнала и является максимально возможным (косинус угла взаимодействия сигнала с самим собой равен 1):Bs(0) = s(t)2 dt = Es.
s(t)2 dt = Es.
Функция АКФ является непрерывной и четной. В последнем нетрудно убедиться заменой переменной t = t-
t в выражении (2.4.1):Bs(t) = s(t) s(t-t) dt =
s(t) s(t-t) dt = s(t-t) s(t) dt = Bs(-t).
s(t-t) s(t) dt = Bs(-t).
С учетом четности, графическое представление АКФ обычно производится только для положительных значений
t. Знак +t в выражении (2.4.1) означает, что при увеличении значений t от нуля копия сигнала s(t+t) сдвигается влево по оси t. На практике сигналы обычно также задаются на интервале положительных значений аргументов от 0-Т, что дает возможность продления интервала нулевыми значениями, если это необходимо для математических операций. В этих границах вычислений более удобным является сдвиг копии сигнала влево по оси аргументов, т.е. применение в выражении (2.4.1) функции s(t-t):Bs(t) =  s(t) s(t-t) dt. (2.4.1')
s(t) s(t-t) dt. (2.4.1')
По мере увеличения значения величины сдвига
t для финитных сигналов временное перекрытие сигнала с его копией уменьшается, а, соответственно, косинус угла взаимодействия и скалярное произведение в целом стремятся к нулю: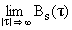 = 0.
= 0.
Пример.
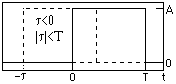
На интервале (0,Т) задан прямоугольный импульс с амплитудным значением, равным А. Вычислить автокорреляционную функцию импульса.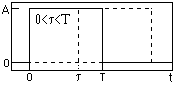 При сдвиге копии импульса по оси t вправо, при 0≤t≤T сигналы перекрываются на интервале от t до Т. Скалярное произведение:
При сдвиге копии импульса по оси t вправо, при 0≤t≤T сигналы перекрываются на интервале от t до Т. Скалярное произведение:
Bs(t) =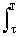 A2 dt = A2(T-t).
A2 dt = A2(T-t).
 При сдвиге копии импульса влево, при -T≤t<0 сигналы перекрываются на интервале от 0 до Т-t. Скалярное произведение:
При сдвиге копии импульса влево, при -T≤t<0 сигналы перекрываются на интервале от 0 до Т-t. Скалярное произведение:
Bs(
t) =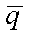 A2 dt = A2(T+t).
A2 dt = A2(T+t).
При |
t| > T сигнал и его копия не имеют точек пересечения и скалярное произведение сигналов равно нулю (сигнал и его сдвинутая копия становятся ортогональными).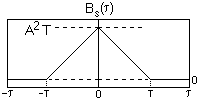 Обобщая вычисления, можем записать:
Обобщая вычисления, можем записать:
Bs(
t) =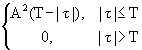 .
.
В случае периодических сигналов АКФ вычисляется по одному периоду Т, с усреднением скалярного произведения и его сдвинутой копии в пределах этого периода:
Bs(t) = (1/Т)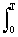 s(t) s(t-t) dt.
s(t) s(t-t) dt.
При
t=0 значение АКФ в этом случае равно не энергии, а средней мощности сигналов в пределах интервала Т. АКФ периодических сигналов при этом также является периодической функцией с тем же периодом Т. Так, для сигнала s(t) = A cos(w0t+j0) при T=2p/w0 имеем:Bs(t) =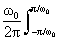 A cos(w0t+j0) A cos(w0(t-t)+j0) = (A2/2) cos(w0t).
A cos(w0t+j0) A cos(w0(t-t)+j0) = (A2/2) cos(w0t).
Отметим, что полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств КФ.
Для сигналов, заданных на определенном интервале [a, b], вычисление АКФ также производится с нормировкой на длину интервала [a, b]:
Bs(t) =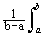 s(t) s(t+t) dt. (2.4.2)
s(t) s(t+t) dt. (2.4.2)
В пределе, для непериодических сигналов с измерением АКФ на интервале Т:
Bs(t) =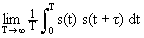 . (2.4.2')
. (2.4.2')
Автокорреляция сигнала может оцениваться и коэффициентом автокорреляции, вычисление которого производится по формуле (по центрированным сигналам):
rs(t) = cos j (t) = б s(t), s(t+t)с /||s(t)||2.
Взаимная корреляционная функция (ВКФ) сигналов (cross-correlation function, CCF) показывает степень сходства сдвинутых экземпляров двух разных сигналов и их взаимное расположение по координате (независимой переменной), для чего используется та же формула (2.4.1), что и для АКФ, но под интегралом стоит произведение двух разных сигналов, один из которых сдвинут на время t:
B12(t) =  s1(t) s2(t+t) dt. (2.4.3)
s1(t) s2(t+t) dt. (2.4.3)
При замене переменной t = t-
t в формуле (2.4.3), получаем:B12(t) = s1(t-t) s2(t) dt =
s1(t-t) s2(t) dt = s2(t) s1(t-t) dt = B21(-t)
s2(t) s1(t-t) dt = B21(-t)
Отсюда следует, что для ВКФ не выполняется условие четности, а значения ВКФ не обязаны иметь максимум при
t = 0. Это можно наглядно видеть на рис. 2.4.1, где заданы два одинаковых сигнала с центрами на точках 0.5 и 1.5. Вычисление по формуле (2.4.3) с постепенным увеличением значений t означает последовательные сдвиги сигнала s2(t) влево по оси времени (для каждого значения s1(t) для подынтегрального умножения берутся значения s2(t+t)).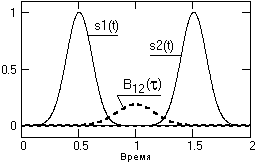
При
t=0 сигналы ортогональны и значение B12(t)=0. Максимум В12(t) будет наблюдаться при сдвиге сигнала s2(t) влево на значение t=1, при котором происходит полное совмещение сигналов s1(t) и s2(t+t). При вычислении значений B21(-t) аналогичный процесс выполняется последовательным сдвигом сигнала s1(t) вправо по временной оси с постепенным увеличением отрицательных значений t, а соответственно значения B21(-t) являются зеркальным (относительно оси t=0) отображением значений B12(t), и наоборот. На рис. 2.4.2 это можно видеть наглядно.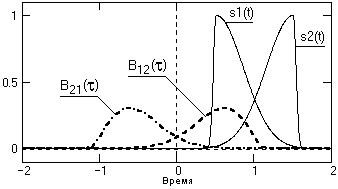
Таким образом, для вычисления полной формы ВКФ числовая ось
t должна включать отрицательные значения, а изменение знака t в формуле (2.4.3) равносильно перестановке сигналов.Для периодических сигналов понятие ВКФ обычно не применяется, за исключением сигналов с одинаковым периодом, например, сигналов входа и выхода систем при изучении характеристик систем.
Коэффициент взаимной корреляции двух сигналов вычисляется по формуле (по центрированным сигналам):
rsv(t) = cos j (t) = б s(t), v(t+t)с /||s(t)|| ||v(t)||. (2.4.4)
Значение коэффициента взаимной корреляции может изменяться от -1 до 1.
2.5. математическое описание шумов и помех
[1, 30].Шумы и помехи
(noise). При детектировании сигналов в сумме с основным информационным сигналом одновременно регистрируются и мешающие сигналы - шумы и помехи самой различной природы. К помехам относят также искажения информационных сигналов при влиянии различных дестабилизирующих факторов на процессы измерений, как, например, влияние микрокаверн в стенках скважины на измерения в рентгенорадиометрических методах каротажа, грозовых разрядов на электроразведочные методы измерений и т.п. Выделение информационных составляющих из зарегистрированных сигналов или максимальное подавление шумов и помех в информационном сигнале при сохранении его полезных составляющих является одной из основных задач первичной обработки сигналов (результатов наблюдений).Если помехи известны и регулярны, как например, фон переменного тока, то борьба с ними особых затруднений не представляет. Наибольшие трудности представляет борьба со случайными (непредсказуемыми) помехами. В общей форме влияние помех на регистрируемый сигнал записывается в следующем виде:
y(t) = V(s(t), q(t)), (2.5.1)
где s(t) – информационная (полезная) часть сигнала, q(t) – помеха.
Помеха называется аддитивной, и обычно именуется шумом, если выражение (2.5.1) представляет собой простую сумму сигнала и помехи:
y(t) = s(t) + q(t). (2.5.2)
Если случайный процесс v(t), оказывающий влияние на сигнал, является неотрицательным, а его влияние выражается в форме:
y(t) = v(t)·s(t), (2.5.3)
то помеху v(t) называют мультипликативной
.В общем случае в сигнале могут присутствовать оба вида помех:
y(t) = v(t) s(t) + q(t). (2.5.4)
Природа помех. Как правило, случайные шумовые помехи (аддитивные) порождаются различного рода физическими флюктуациями – случайными отклонениями тех или иных физических величин от своих средних значений. Природа флюктуаций обычно определяется статистической природой физических процессов. Многие физические величины представляют собой результаты усреднения определенных параметров физических процессов, дискретных и случайных по своей природе. Так, например, тепловой шум регистрируемого напряжения на резисторах электрических цепей обуславливается флюктуациями теплового движения носителей зарядов - случайностью процесса дрейфа отдельных электронов по резистору, по суммарной интенсивности движения которых и формируется падение напряжения на резисторе. Дискретной является природа электромагнитных видов излучения – дискретный квант энергии излучения (фотон) определен значением hn, где h – постоянная Планка, n - частота. Флюктуации физических величин, дискретных и случайных по своей природе, принципиально неустранимы, и речь может идти только о том, чтобы уменьшать их относительную величину имеющимися в нашем распоряжении средствами.
Природа мультипликативных помех обычно связана с изменениями условий измерений, параметров каналов передачи данных и систем их обработки, т.е. когда случайные помехи накладываются не на сам сигнал непосредственно, а на системы, в которых этот сигнал формируется и обращается, вызывая опосредствованные искажения сигнала, как линейные, так и нелинейные.
Характеристики помех. В математическом описании помехи представляются случайными функциями времени. Случайную функцию непрерывного времени обычно называют случайным процессом, ее дискретный аналог – случайной последовательностью. Как правило, помехи относятся к классу стационарных случайных процессов, и характеризуются своими распределениями и моментами распределений, как их числовыми параметрами. Основное распределение большинства шумовых сигналов – нормальное (гауссов процесс). Это объясняется тем, что распределение сумм независимых случайных величин, из которых складываются случайные помехи, сходится к нормальному, вне зависимости от характера распределения слагаемых (теорема Ляпунова).
Момент первого порядка выражает среднее значение (постоянную составляющую) случайного процесса. Теоретическое значение и оценка момента (по интервалу [a, b]):
M{q} = 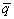 =
= q·p(q) dq. (2.5.5)
q·p(q) dq. (2.5.5)
где p(q) – плотность вероятностей значений q.
Центральный момент второго порядка определяет дисперсию процесса:
D{q} = s2 = (q-
(q-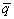 )2·p(q) dq =
)2·p(q) dq = 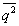 -
- 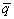 2. (2.5.6)
2. (2.5.6)
Дисперсия выражает мощность переменной составляющей процесса. Корень квадратный из значения дисперсии, т.е. значение
s, является средним квадратическим значением разброса случайных значений q относительно среднего значения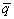 .
.
Смешанный момент второго порядка называется функцией автокорреляции случайного процесса q(t):
M{q(t)q(t+t)} =
 x1x2·p(x1,x2) dx1 dx2 = B(t). (2.5.7)
x1x2·p(x1,x2) dx1 dx2 = B(t). (2.5.7)
Величина B(
t) при t = 0 равна общей мощности случайного процесса q(t).На практике большинство случайных процессов обладают свойством эргодичности. Оно заключается в том, что средние значения по множеству реализаций (математические ожидания, вычисляемые по плотностям распределений (2.5.5-7)) совпадают со средними значениями по времени Т одной реализации процесса при Т
Ю Ґ . Это позволяет производить оценку числовых значений параметров помех непосредственно по произвольным интервалам [a, b] задания сигналов: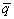 =
= 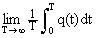 »
» 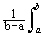 q(t) dt. (2.5.8)
q(t) dt. (2.5.8)
s
2=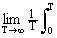 (q(t)-
(q(t)-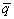 )2 dt »
)2 dt » 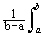 (q(t)-
(q(t)-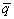 )2 dt. (2.5.9)
)2 dt. (2.5.9)
B(t)
=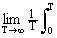 q(t)q(t+t) dt »
q(t)q(t+t) dt » 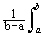 q(t)q(t+t) dt. (2.5.10)
q(t)q(t+t) dt. (2.5.10)
Спектральная плотность мощности случайного процесса (распределение мощности помех и шумов по частоте) связано с функцией автокорреляции преобразованием Фурье. В одностороннем (физическом) представлении спектра:
B(
f) = 4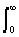 B(t) cos 2pft dt. (2.5.11)
B(t) cos 2pft dt. (2.5.11)
B(t)
=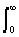 B(f) cos 2pft dt. (2.5.12)
B(f) cos 2pft dt. (2.5.12)
Аддитивную помеху с равномерным спектром
B(f) = B0 = const
называют белым шумом. Мощность белого шума в полосе частот 0-F пропорциональна ширине полосы:
WF =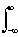 B(f) df = BoF.
B(f) df = BoF.
При белом шуме полоса частот всегда полагается конечной, т.к. в противном случае мы получим бесконечную мощность шумов.
Сигнал с аддитивной помехой обычно характеризуют не абсолютной мощностью помехи, а отношением средних мощностей сигнала и помехи, которое кратко называют отношением сигнал/помеха
:r =
Wc/Wq.Значения случайных процессов являются некоррелированными только при неограниченной полосе частот. Любое ограничение частотной полосы вносит определенную корреляцию в процесс и независимыми друг от друга можно считать только значения процесса, отстоящие друг от друга как минимум на интервал корреляции
to:t
o = (2/WF)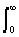 B(t) dt = 1/2F.
B(t) dt = 1/2F.
литература
1. Баскаков С.И. Радиотехнические цепи и сигналы
: Учебник для вузов. - М.: Высшая школа, 1988.3. Васильев Д.В. Радиотехнические цепи и сигналы: Учебное пособие для вузов. - М.: Радио и связь, 1982. - 528 с.
11. Зиновьев А.Л., Филиппов Л.И. Введение в теорию сигналов и цепей: Учебное пособие для вузов. - М.: Высшая школа, 1975. - 264 с.
16. Макс Ж. Методы и техника обработки сигналов при физических измерениях: В 2-х томах.- М.: Мир, 1983.
25. Сергиенко А.Б. Цифровая обработка сигналов. / Учебник для вузов. – СПб.: Питер, 203. – 608 с.
29. Сато Ю. Обработка сигналов. Первое знакомство. – Изд.: ДОДЭКА, 2002.
30. Харкевич А.А. Борьба с помехами. – М.: Наука, 1965.
Copyright ©2005 Davydov А.V.
Усталость света, анг. tired light - это явление потери энергии квантом электромагнитного излучения при прохождении космических расстояний, то же самое, что эффект красного смещения спектра далеких галактик, обнаруженный Эдвином Хабблом в 1926 г.
На самом деле кванты света, проходя миллиарды световых лет, отдают свою энергию эфиру, "пустому пространству", так как он является реальной физической средой - носителем электромагнитных колебаний с ненулевой вязкостью или трением, и, следовательно, колебания в этой среде должны затухать с расходом энергии на трение. Трение это чрезвычайно мало, а потому эффект "старения света" или "красное смещение Хаббла" обнаруживается лишь на межгалактических расстояниях.
Таким образом, свет далеких звезд не суммируется со светом ближних. Далекие звезды становятся красными, а совсем далекие уходят в радиодиапазон и перестают быть видимыми вообще. Это реально наблюдаемое явление астрономии глубокого космоса. Подробнее читайте в FAQ по эфирной физике.
|
|
