ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ВОЗДЕЙСТВИЯ МАССОДИНАМИЧЕСКИХ ПОЛЕЙ НА ПРОЦЕСС СВОБОДНЫХ КОЛЕБАНИЙ МАЯТНИКА

доктор технических наук, профессор

Контакт с автором: samohvalov_vn@mail.ru

Аннотация

Представлены результаты исследований процесса свободных колебаний маятника, экспериментально подтверждающие существование массодинамического (гравидинамического) поля. Проведен анализ влияния массодинамических полей Земли, Луны и Солнца на процесс колебаний маятника и поворот его плоскости.

_____________________________________________________________

Первые опыты с физическим маятником поставлены Жаном Фуко в 1851г. в Пантеоне Парижа. Длина маятника была 67 м, вес – 28 кг. Обычное наблюдавшееся отклонение маятника в течении времени суток – 15 град/час объяснялось действием Кориолисова ускорения. Однако в опытах Морриса Алле, проводившихся в 1954-1960 годах с использованием параконического маятник длиной около одного метра, обнаружены аномалии движения маятника [1]. В ходе наблюдений отмечены весьма значительные аномалии при отсутствии какого-либо магнитного поля, за исключением поля Земли, а именно - наличие существенной периодичности порядка 24 часов 50 минут. В продолжении этих работ исследователями НАСА во время солнечного затмения 1999г. в обсерватории австрийского монастыря ордена бенедектинцев в Кренсмюнстере отмечено, что скорость изменения траектории колебаний маятника Фуко (длиной 50 м) при затмении возросла в два раза [2].

Теоретические предположения о существовании в природе полей гравитационной природы, аналогичных по своему действию магнитным полям, впервые высказанные А. Эйнштейном были развиты в работах Г.Тирринга и Й.Лензе, Н.В Мицкевича, А.И. Фока, Ю.С Владимирова и др. [4-8]. Теоретические исследования в области гравидинамических (гравимагнитных, массодинамических) полей отражены в достаточно большем количестве электронных публикаций Адаменко А., Кадырова С.К., Коновалова В.К., Меркулова В.И., Плотникова С.В., Телегина М.Б., Уварова В.В., Хлынцева В.П., Чуева А.С. и др.

Массодинамические (гравимагнитные, гравидинамические) поля околоземного пространства должны воздействовать на любой движущийся в них материальный объект (массу), аналогично тому как магнитное поле действует на движущийся относительно него электрически заряженный объект (электрический заряд). Однако достаточных экспериментальных доказательств существования этих полей нет.

Ниже представлены некоторые результаты экспериментов с маятником, выполненных автором в период с 06.09.1999г по 16.10.2000г, опубликованные в приложении к [3], показывающие принципиальные отличия в поведении маятника от описываемого теорией, учитывающей только действие гравитации и Кориолисова ускорения. Проявление всех обнаруженных эффектов в поведении маятника обусловлено действием на него изменяющихся во времени масссодинамических сил.

1 Методика проведения экспериментов

В качестве датчика, фиксирующего наличие и величину внешнего массодинамического поля, может быть использован любой движущийся материальный объект. При проведении экспериментов датчиком был маятник. Это обусловлено тем тем, что маятник совершая циклические движения способен накапливать даже малые постоянные воздействия внешних сил, суммируя их и делая заметным эффект от их воздействия.

Для экспериментального обнаружения массодинамических полей был использован тяжелый маятник малой относительной длины L* =L/А_0@2,182, где А₀ – начальная амплитуда маятника, L – длина маятника. Длина маятника L=2400мм, максимальная начальная амплитуда А₀=1100мм (максимальная начальная относительная амплитуда колебаний маятника А* =А₀/L @ 0,458). Маятник, применявшийся в эксперименте: свинцовый цилиндр диаметром 55мм и массой 2,9 кг, подвешенный на тонкой струне. Струна: тонкий пучок нескрученных синтетических волокон (распущенная нить) длиной 120 мм, одним концом заделанный в фильеру в точке подвески, а другим концом скрепленный с нихромовой проволокой диаметром 0,4 мм, которая через тонкую нить связана со свинцовым цилиндром. Заделка тонкого пучка волокон в фильеру позволила практически исключить различие во влияние подвески на процесс колебаний маятника в любой из возможных плоскостей.

Характер и величина воздействия на движущуюся массу (маятник) со стороны массодинамического поля будет при этом определяться как начальным расположением плоскости качания маятника по отношению к оси Земли, так и картиной силовых линий суммарного массодинамического поля вблизи поверхности земли (в области качания маятника), соответствующей текущему моменту времени [3].

Эксперименты проводились в г. Самара (53° 13¢ с.ш., 50° 9¢ в.д.). Маятник был подвешен в закрытом помещении на втором этаже деревянного здания.

2 Экспериментальные исследования движения плоскости качания маятника

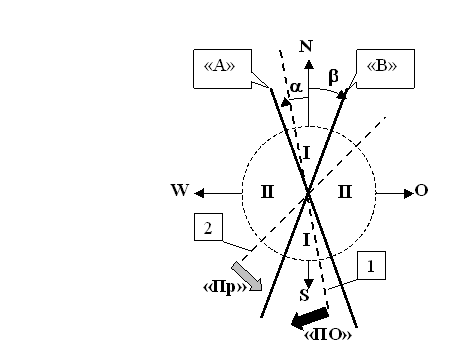
Проведенные эксперименты показали, что при большой начальной относительной амплитуде маятника, в диапазоне больших текущих амплитуд колебаний маятника (А* ³ 0,25) существуют два сектора “i ” и “i i ”(рисунок 1), в которых поведение маятника, в процессе его колебаний, качественно отличается. На рисунке 1 линия “N-S” - меридиональная плоскость (север- юг), линия “W-O” - запад-восток.

Если задавалась начальная плоскость колебаний маятника в секторе “i ”, т.е. между линиями “А” и “В” (поз 1, рисунок 1), то в процессе его колебаний, возникал поворот плоскости качания маятника по часовой стрелке “ПО”, а также, в ряде случаев, заметный эллипс движения маятника в горизонтальной плоскости с вращением в туже сторону.

Рисунок 1

Если же начальная плоскость колебаний маятника задавалась в секторе “i i ” (поз.2, рисунок 1), то наблюдался поворот плоскости качания маятника против часовой стрелки “Пр” и значительный эллипс движения маятника также против часовой стрелки.

Если же начальная плоскость колебаний маятника задавалась на границе секторов “i ” и “i i ” (по линии “А” или “В”), то имела место относительно длительная устойчивость заданного начального положения плоскости качания маятника (отсутствие эллипса движения маятника в процессе его колебаний и отсутствие поворота плоскости качания).

При этом линия “А” была плоскостью “неустойчивого” равновесия. Даже небольшое отклонение заданной начальной плоскости колебаний маятника от линии “А” приводила к нарастанию этого отклонения. Наблюдалось возникновение эллипса движения маятника и поворот плоскости его качания от линии “А”.

Линия “В” напротив была плоскостью “устойчивого” равновесия. При небольшом отклонение начальной плоскости колебаний маятника от линии “В”, плоскость качания маятника поворачивалась по направлению к ней, уменьшая начальное отклонение. При этом наблюдался небольшой переход точки равновесия и обратный ход плоскости качания маятника к линии “В”.

По результатам большого числа опытов было установлено, что углы a (угол между меридианом и линией “А”) и b (угол между меридианом и линией “В”, рисунок 1) не являются константами, т.е изменятся во времени.

Результаты экспериментальных исследований (рисунки 2 - 8) показали весьма значительное изменение углов a и b , определяющих положение плоскостей относительной устойчивости колебаний маятника “А” и “В”, в течение времени суток, дней лунного цикла и т.д. Анализ результатов экспериментов показал следующее:

1. Величина углов a и b изменялась одновременно (рисунок 2). При этом изменение углов имело один знак – одновременно уменьшение или увеличение. Однако величина угла j =½ a ½ -½ b ½ ¹ 0 изменялась в течение времени, т.е. скорость изменения углов a и b была разной и центр сектора “i” (рисунок 1) не всегда совпадал с меридианом (j =0 при ½ a ½ =½ b ½ ).

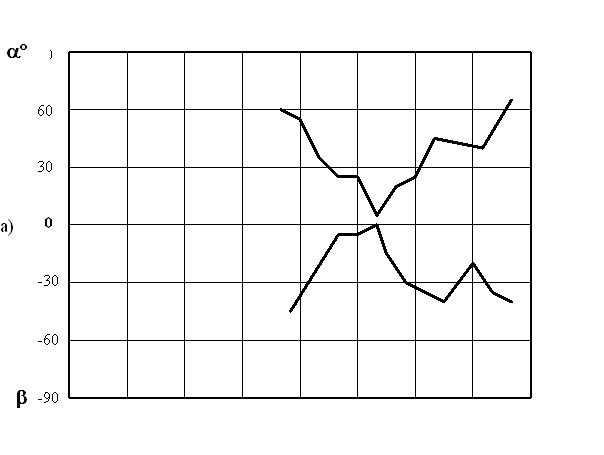
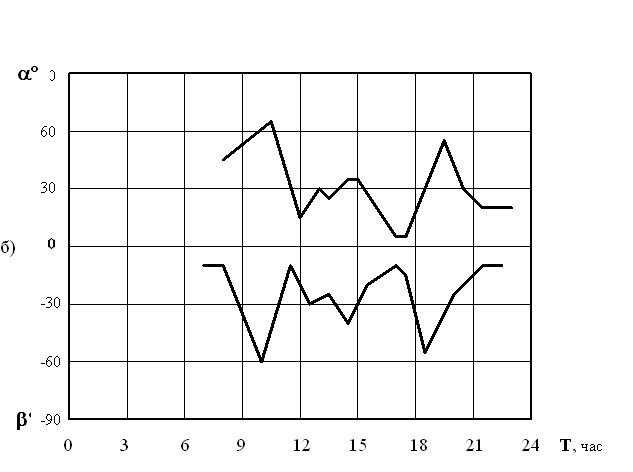
Рисунок 2 – Изменение углов a и b в течении времени суток

а) 30.08.2000г., 1-й день после новолуния, б) 31.08.2000г., 2-й день после новолуния

2. Величина изменения углов a и b в течение суток достигала 60 и более градусов. В отдельные моменты времени скорость изменения величины углов достигала 40 и более градусов в час (например, см. рисунок 2).

3. Зависимость величины углов a и b от времени суток в каждый последующий день существенно изменялась по сравнению с предыдущим днем (рисунок 2а и 2б - соответственно 30 и 31 августа 2000г., рисунок 3 – 19, 20 и 21 сентября 2000г.).

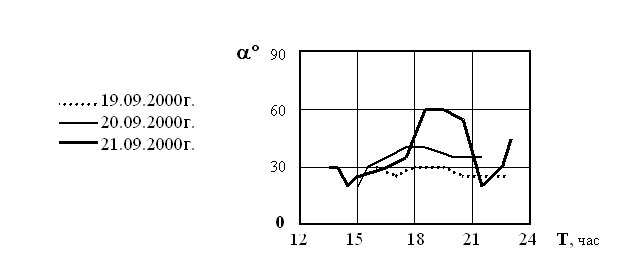
Рисунок 3 – Изменение угла a в течении времени суток в разные дни

4. В течение суток в различные дни наблюдались периоды резкого изменения углов a и b , а также периоды относительной стабильности (рисунок 4).

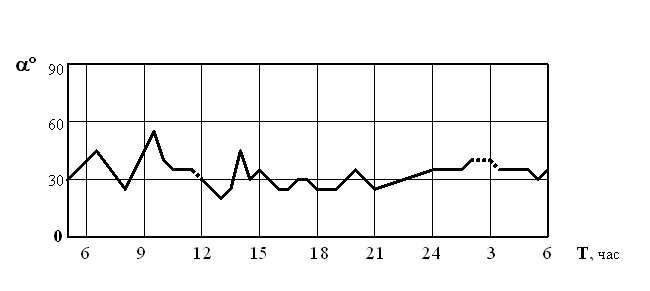
5. В отдельные моменты времени имели место “неустойчивость” процесса поворота плоскости качания маятника и “неопределенность” величин углов a и b (рисунки 5 и 6).

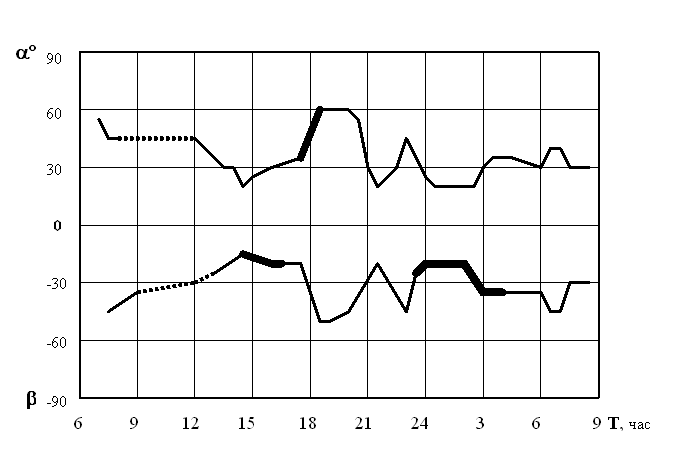
В периоды “неустойчивости” небольшие погрешности в момент запуска маятника оказывали определяющее влияние на последующий поворот плоскости качания маятника.

В периоды “неопределенности” происходило изменение направления поворота плоскости качания с начального “ПО” на большой амплитуде на “Пр”, при ее уменьшении. Этот эффект наблюдался в диапазоне 5…10° как для a так и для b .

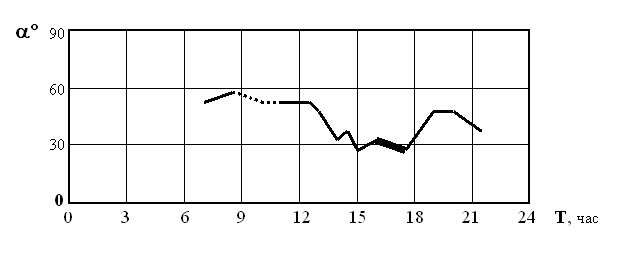
6. В дни новолуний и полнолуний, в периоды резкого изменения величин углов a и b направление этих изменений было противоположного знака (рисунок 7)

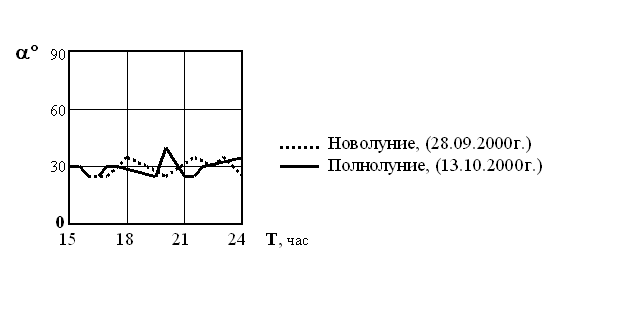
Рисунок 7 – Изменение угла a в дни новолуния и полнолуния

7. При затухании колебаний маятника (А* £ 0,2), в ряде случаев, наблюдалась смена знака вращения плоскости колебаний маятника: появление вращения “ПО” в зоне ii (рисунок 1) и наоборот.

3 Анализ силовых воздействий на маятник

При колебаниях маятника на него действуют следующие силы.

Силы, обусловленные гравитационными полями Земли, Луны и Солнца. Величина этих сил, действующая на маятник для фиксированного момента времени, зависит только от массы маятника и суммарной величины ускорения свободного падения.
Кориолисова и центробежная силы, обусловленные вращением Земли вокруг своей оси, как геометрической системы. Эти силы возникают как реакции при наличии связей, препятствующих свободному перемещению движущейся массы в этой системе. Величина этих сил, действующих на маятник, зависит как от массы маятника, так и от величины и направления вектора скорости движения маятника в процессе его колебаний.
Силы, обусловленные воздействием на движущуюся массу маятника массодинамических полей. Величина массодинамической силы F_МД (при движении массы в массодинамичесом поле) определяется аналогично силе Лоренца (при движении электрического заряда в магнитном поле) [3]:

F_МД=m× VЧH_МД ,

где, m -- масса тела, V - скорость его движения, H_МД - напряженность массодинамического поля.

Величина этих сил, действующих только на движущейся маятник, зависят (при прочих равных условиях) не только от его массы (как для кориолисовой и центробежной сил), но и от массы объектов генерирующих соответствующие массодинамические поля, т.е. массы Земли, Луны, Солнца [3]. Кроме того, эти силы зависят от расстояний до этих объектов, скоростей их относительного перемещения и их взаимного расположения по отношению к Земле (т.к. изменяется результирующая напряженность суммарного массодинамического поля [3].

Гравитационное поле Земли в области качания маятника, при фиксированном положении точки подвески маятника относительно поверхности земли (вследствие относительной малости как вертикальной, так и горизонтальной составляющих амплитуды колебаний), является практически постоянным для рассматриваемой системы и не может влиять на изменение параметров поворота плоскости качания маятника в различные моменты времени. Влияние гравитационных полей Луны и Солнца на этот процесс также практически исключено. Это обусловлено существенной их малостью по сравнению с гравитационным полем Земли (для рассматриваемой системы). Кроме того, их воздействие может в принципе изменять только положение точки равновесия маятника (в системе координат жестко связанной с поверхностью земли), но не может влиять на процесс поворота плоскости качания свободного маятника, т.к. эти силы не зависят от величины и направления вектора скорости движения маятника. Результирующая гравитационная сила, действующая на маятник, не зависит от величины и направления вектора скорости движения маятника и направлена вертикально вниз (по линии отвеса). Поэтому влияние гравитационных сил на возникновение эффекта изменения направления и скорости поворота плоскости качания маятника исключается.

Воздействия кориолисовой и центробежной сил на процесс колебания свободного маятника (при неизменности его параметров) является постоянным и не зависит от времени суток, фаз Луны и времени года.

Исходя из этого, кориолисова и центробежная силы, оказывая влияния на сам процесс колебания маятника и поворот плоскости качания маятника, не могут являться причинами, вызывающими эффект изменения в течение времени величины углов a и b (ширины секторов i и ii - рисунок 1). Следовательно, причиной изменения углов a и b может является действие на маятник только массодинамических сил, изменяющихся во времени.

Поскольку параметры вращения Земли вокруг своей оси практически неизменны, то напряженность массодинамического поля Земли в конкретной точке на ее поверхности постоянна. При этом, как показано в работе [3], горизонтальная (меридиональная) составляющая напряженности собственного массодинамического поля вращающейся Земли направлена с севера на юг, а вертикальная составляющая - снизу вверх. В результате массодинамическая сила от вертикальной составляющей напряженности массодинамического поля направлена в одну сторону с Кориолисовой силой, а составляющая от горизонтальной составляющей - против нее.

Однако, суммарное массодинамическое поле, в пространстве, где расположен маятник, включает также массодинамические поля вращения Луны вокруг Земли, вращения Земли вокруг Солнца и собственного вращения Солнца вокруг оси. Напряженность этих полей в конкретной точке на поверхности земли переменны в течение времени, вследствие изменения положения Солнца и Луны, а, следовательно, величины и направления силовых линий этих массодинамических полей относительно плоскости качания маятника. Вследствие суточного вращения Земли, наклона оси Земли к плоскости ее солнечной орбиты и плоскости лунной орбиты происходит непрерывное изменение параметров суммарного массодинамического поля. При этом изменяется как величина меридиональной и вертикальной составляющей напряженности суммарного массодинамического поля, так и возникновение ее широтной составляющей. Следствием этого является изменение во времени величины и направления массодинамической силы, действующей на маятник в процессе его колебаний. В результате в каждый момент времени, для определенных положений плоскости колебаний маятника (линии “А” и “В”), действие массодинамических сил уравновешивает действие кориолисовой и центробежной сил и имеет место стабильное положение плоскости колебаний маятника (без ее поворота в течение определенного времени).

В этот же момент времени, для других положений начальной плоскости колебаний маятника, эти силы не скомпенсированны и происходит поворот плоскости качания маятника. Направлении вращения плоскости колебаний маятника или совпадает с направлением поворота от действия кориолисовой силы, или становится противоположным ему – если силовой эффект от действия массодинамических сил превышает силовое воздействие кориолисовой силы. В результате изменения в течении времени напряженности суммарного массодинамического поля, значения углов a и b , определяющих положение плоскостей “А” и “В”, а также величину секторов “i” и “ii”, в течение времени так же непрерывно изменяются, что зафиксировано в проведенных экспериментах.

4 Выводы из результатов экспериментальных исследований

Анализ результатов проведенных исследований позволил сделать выводы:

Наблюдавшиеся эффекты в поведении маятника обусловлены существованием массодинамического поля и изменением во времени его напряженности.
Вследствие вращения Земли вокруг своей оси и ее наклона к плоскости земной орбиты, в течение суток происходит изменения положения точки на поверхности земли, где подвешен маятник, и плоскости его качания по отношению к Луне и Солнцу и, следовательно, направлению силовых линий суммарного массодинамического поля [3]. Это приводит к непрерывному изменению в течение суток величины массодинамических сил, действующих на маятник для каждого фиксированного положения начальной плоскости его качания.
Вследствие вращения Луны вокруг Земли, эллипса и наклона плоскости лунной орбиты к земной оси, в один фиксированный момент времени суток, но в различные дни (фазы) лунного цикла, в точке пространства, где подвешен маятник, имеют место различные по величине и направлению векторы напряженности массодинамического поля вращения Луны вокруг Земли. Это приводит к непрерывному изменению в течение лунного месяца величины соответствующих массодинамических сил, действующих на маятник в каждый фиксированный момент времени суток.
Вследствие вращения Земли вокруг Солнца, эллипса орбиты Земли и наклона земной оси к плоскости ее орбиты, в течение года изменяется угол между вектором скорости вращения Земли и радиус-вектором на Солнце. Из-за этого в течение года (для каждого фиксированного времени земных суток в заданной точке подвески маятника) изменяются горизонтальные и вертикальные, а также широтные и меридиональные составляющиенапряженности массодинамических полей вращения Земли вокруг Солнца и массодинамического поля вращения Солнца вокруг оси.

При этом, как это показали исследования, результаты наблюдений “эффекта маятника” в одни дни (фазы) ближайших лунных циклов имеют качественное сходство, но количественно не совпадают.

Это обусловлено следующим:

длительность лунного цикла не кратна земным (солнечным) суткам, т.е. одни и те же лунные фазы наступают в разные месяцы в различное время суток;
из-за наклона Земной оси к плоскости ее орбиты, в течение различных месяцев года для каждой одинаковой фазы Луны и фиксированного момента времени суток будет иметь место различная величина угла между земной осью и радиус-вектором на Солнце.

Картина суммарного массодинамического поля в каждый день года, в течение многих лет, в один и тот же момент времени будет также отличаться, т.к. не кратны между собой период вращения Земли вокруг своей оси, период вращения Луны вокруг Земли и период вращения Земли вокруг Солнца. Таким образом, картина суммарного массодинамического поля (в конкретной точке на поверхности земли) в течение времени количественно практически не повторяется, но в течение месячного и годового циклов повторяются качественные закономерности изменения параметров движения плоскости качания маятника.

Исходя из вышеизложенного, дополнительное воздействие массодинамических сил на качающийся свободный маятник и обуславливает “эффект маятника”. Это обстоятельство является экспериментальным доказательством существования массодинамических полей, как одного из видов физических полей.

Литература

Алле М. О моих экспериментах по физике. 1952-1960 годы. К статье “Философия моей жизни”.
Козлов Ю. Загадка природы ждет своего объяснения. // Газета “Сегодня” Киев, 31.05.2000.
Самохвалов В.Н. Теория физических полей / И.П. №72200100015. //Инф.Бюл. Идеи. Гипотезы. Решения. - М.:ВНТИЦ.- 2001.- №2.- с.13 (2001.02.0053).
Einstein A. Vietelj Schrift Cer. Medizin. - 1912.Bd44.- S.37(T.1.-C.223)
Владимиров Ю. С., Мицкевич Н.В. Пространство, время, гравитация. - М. : Наука, 1969г.;
3.Thirring H., Lense J. Phys. Z. - 1918. - Bd19.- S.156.
Мицкевич Н.В. Физические поля в общей теории относительности. - М.: Наука, 1969.
Фок А.И. Теория пространства, времени и тяготения. - М.: Госиздат,1961.

к библиотеке В. Н. Самохвалов

Знаете ли Вы, что в 1974 - 1980 годах профессор Стефан Маринов из г. Грац, Австрия, проделал серию экспериментов, в которых показал, что Земля движется по отношению к некоторой космической системе отсчета со скоростью 360±30 км/с, которая явно имеет какой-то абсолютный статус. Естественно, ему не давали нигде выступать и он вынужден был начать выпуск своего научного журнала "Deutsche Physik", где объяснял открытое им явление. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира