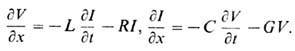
Телеграфные уравнения - ур-ния в частных производных, описывающие процесс распространения
эл--магн. волн в линиях передачи (в коаксиальных кабелях, двухпроводных
линиях и др.):
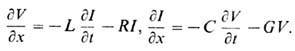
Здесь V(х, t)и
I(x, t)- напряжение и ток в линии; L и С- погонные (на
единицу длины) индуктивность и ёмкость, зависящие от сечения проводов, расстояния
между ними и свойств заполняющей среды; R и G - погонные сопротивление
и проводимость, учитывающие токи утечки. Структура эл--магн. поля в поперечном
сечении линии предполагается квазистационарной, что выполняется для волн с длиной,
существенно большей поперечных размеров линии. Телеграфные уравнения приближённо описывают также
распространение сигналов в линиях, состоящих из сосредоточенных ёмкостей, индуктивностей
и сопротивлений при условии, что
различия величин V и I на соседних звеньях достаточно малы. В
идеализированном случае, когда R = 0, G = 0, эл--магн. сигналы
распространяются вдоль линии со скоростью u=1/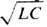
без искажения и затухания. Если L и С зависят от частоты w, то
телеграфные уравнения справедливы только для гармонич. волн и записываются для комплексных амплитуд
тока I и напряжения V, так что дI/дt и дV/дt заменяются
соответственно на iwI и iwV.
Знаете ли Вы, что в 1974 - 1980 годах профессор Стефан Маринов из г. Грац, Австрия, проделал серию экспериментов, в которых показал, что Земля движется по отношению к некоторой космической системе отсчета со скоростью 360±30 км/с, которая явно имеет какой-то абсолютный статус. Естественно, ему не давали нигде выступать и он вынужден был начать выпуск своего научного журнала "Deutsche Physik", где объяснял открытое им явление. Подробнее читайте в FAQ по эфирной физике.
без искажения и затухания. Если L и С зависят от частоты w, то
телеграфные уравнения справедливы только для гармонич. волн и записываются для комплексных амплитуд
тока I и напряжения V, так что дI/дt и дV/дt заменяются
соответственно на iwI и iwV. 
