к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

РЕАЛЬНАЯ ФИЗИКА

Глоссарий по физике

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

Роша предел

Роша предел - расстояние от планеты (звезды) до её спутника, ближе к-рого спутник разрушается приливными силами. При движении спутника по орбите вокруг планеты (звезды) сила её притяжения, действующая на элемент спутника, компенсируется центробежной силой только в его центре масс. Во всех др. точках спутника такого равенства нет, что и обусловливает приливную силу.

Р. п. назван по имени Э. Роша, поставившего и разрешившего (1847) [1] проблему равновесия жидкого, бесконечно малого (по размерам и массе), несжимаемого, однородного, самогравитирующего спутника, равномерно вращающегося в экваториальной плоскости планеты конечной массы (период осевого вращения спутника предполагался равным орбитальному периоду). Рош показал, что под действием приливных сил спутник приобретает эллипсоидальную форму и существует такое расстояние D от центра планеты, ближе к-рого спутник уже не может находиться в равновесии (разрывается приливными силами). Это расстояние (т. н. классич. Р. п.) зависит от радиуса планеты (R) и плотностей планеты и спутника

Применяя результаты своих исследований к системе Сатурна, Рош пришёл к заключению, что кольца Сатурна должны состоять из мелких частиц, т. к. радиус наружного края внеш. кольца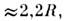 т. е. меньше D (в предположении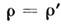). В данном случае Рош пришёл к верному заключению, исходя из неверных предпосылок, т. к. Р. п. для твёрдого спутника может существенно отличаться от классич. Р. п.

Р. п. для твёрдых тел зависит от их размеров и прочности. При изучении Р. п. для таких тел выделяются два типа разрушения: пластическое (вследствие среза) и хрупкое (вследствие отрыва). Для хрупких тел наступление разрушения удовлетворительно описывается критерием наибольших нормальных напряжений, для пластичных - критерием наибольших касательных напряжений (см. Прочности предел). Применяя критерий наибольших касательных напряжений и полагая прочность тел Т = 10⁹ дин/см² (что соответствует прочности гранита}. X. Джефрис [2] определил макс. размер тел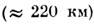 , не разрушающихся при пролёте вблизи Земли. Однако этот размер может быть и меньше, если тело близко по структуре к хондритам (см. Метеориты)с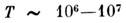 дин/см². Более поздние исследования [3] показали, в частности, что макс. радиус тел с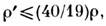 не разрушающихся при движении по орбите волизи поверхности планеты, 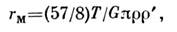а Р. п. для тел с радиусами более 30 км и T = 10⁶ дин/см²составляет (1,35-1,38)R (при орбитальном движении) и (1,16-1,19) R (при свободном падении на поверхность планеты). Из-за наличия трещин и неоднородностей реальное тело разрушается сложным образом, и по мере приближения к планете возможно неоднократное дробление осколков.

Теория приливного разрушения тел позволяет, в частности, объяснить наличие близко расположенных (двойных) кратеров на современных поверхностях Земли, Луны и Марса. Земля и др. планеты образовались в результате объединения большого числа твёрдых допланетных тел (см. Происхождение Солнечной системы). Прежде чем упасть на растущую планету, допланетное тело испытывает неск. близких сближений с ней. Достаточно крупное тело может быть разрушено приливными силами, при этом его осколки падают в разные, но близко расположенные точки поверхности планеты, образуя двойные кратеры.

Приливные эффекты играют существ. роль также в двойных звёздных системах, в к-рых расстояния между звёздами сравнимы с их размерами (см. Тесные двойные звёзды, Полость Роша).

Литература по пределу Роша

Roche Е., Memoire sur la figure d'une masse fluide, soumise a Г attraction d'un point eloigne, в кн.: Academie des sciences et lettres de montpellier. Memoires de la Section des Sciences, v. 1-2, [P.], 1847-50;
Jeffreys H., Tbe relation of cohesion to Roche's limit, «Monthly Notices Roy. Astron. Soc.», 1947, v. 107, № 3, p. 260;
Aggarwal H. R., Оberbесk V. R., Roche limit of a solid body, «Astrophys. J.», 1974, v. 191, p. 577.

В. В. Леонтьев

к библиотеке к оглавлению FAQ по эфирной физике ТОЭЭ ТЭЦ ТПОИ ТИ

Знаете ли Вы, что только в 1990-х доплеровские измерения радиотелескопами показали скорость Маринова для CMB (космического микроволнового излучения), которую он открыл в 1974. Естественно, о Маринове никто не хотел вспоминать. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира