Закон излучения Планка (формула Планка) - закон распределения энергии в
спектре излучения
равновесного при определённой температуре Т. Был открыт
М. Планком (М. Planck) в 1900 на основе гипотезы квантования энергии вещества.
Планк моделировал вещество совокупностями гармонических осцилляторов различной
частоты v - резонаторов,
испускающих и поглощающих излучение
соответствующей частоты. Он предположил, что энергия вещества распределяется по
резонаторам каждой частоты v в виде дискретных порций hv - квантов
энергии (h - Планка постоянная).
Планка закон излучения является частным случаем распределения Бозе
(см. Бозе статистика).
Планка закон излучения даёт спектральную зависимость
(зависимость от частоты v или длины волны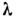 =
c/v)
объёмной плотности излучения (энергии излучения в единице объёма) и пропорциональной
ей испускат. способности абсолютно чёрного тела
=
c/v)
объёмной плотности излучения (энергии излучения в единице объёма) и пропорциональной
ей испускат. способности абсолютно чёрного тела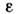 =
сu/4 (энергии излучения, испускаемой единицей его поверхности за единицу
времени). функции uv,T и
=
сu/4 (энергии излучения, испускаемой единицей его поверхности за единицу
времени). функции uv,T и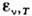 (или
(или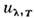 и
и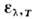 ), отнесённые
к ед. интервала частот (или длин волн), являются универсальными функциями
от v (или
), отнесённые
к ед. интервала частот (или длин волн), являются универсальными функциями
от v (или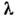 )
и Т, не зависящими от природы вещества, с к-рым излучение находится
в равновесии.
)
и Т, не зависящими от природы вещества, с к-рым излучение находится
в равновесии.
Планка закон излучения выражается формулой
и полной испускат. способности чёрного тела
Знаете ли Вы, что электромагнитное и другие поля есть различные типы колебаний, деформаций и вариаций давления в эфире.
Понятие же "физического вакуума" в релятивистской квантовой теории поля подразумевает, что во-первых, он не имеет физической природы, в нем лишь виртуальные частицы у которых нет физической системы отсчета, это "фантомы", во-вторых, "физический вакуум" - это наинизшее состояние поля, "нуль-точка", что противоречит реальным фактам, так как, на самом деле, вся энергия материи содержится в эфире и нет иной энергии и иного носителя полей и вещества кроме самого эфира.
В отличие от лукавого понятия "физический вакуум", как бы совместимого с релятивизмом, понятие "эфир" подразумевает наличие базового уровня всей физической материи, имеющего как собственную систему отсчета (обнаруживаемую экспериментально, например, через фоновое космичекое излучение, - тепловое излучение самого эфира), так и являющимся носителем 100% энергии вселенной, а не "нуль-точкой" или "остаточными", "нулевыми колебаниями пространства". Подробнее читайте в FAQ по эфирной физике.
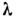 =
c/v)
объёмной плотности излучения (энергии излучения в единице объёма) и пропорциональной
ей испускат. способности абсолютно чёрного тела
=
c/v)
объёмной плотности излучения (энергии излучения в единице объёма) и пропорциональной
ей испускат. способности абсолютно чёрного тела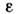 =
сu/4 (энергии излучения, испускаемой единицей его поверхности за единицу
времени). функции uv,T и
=
сu/4 (энергии излучения, испускаемой единицей его поверхности за единицу
времени). функции uv,T и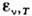 (или
(или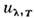 и
и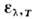 ), отнесённые
к ед. интервала частот (или длин волн), являются универсальными функциями
от v (или
), отнесённые
к ед. интервала частот (или длин волн), являются универсальными функциями
от v (или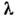 )
и Т, не зависящими от природы вещества, с к-рым излучение находится
в равновесии.
)
и Т, не зависящими от природы вещества, с к-рым излучение находится
в равновесии.
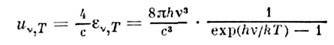
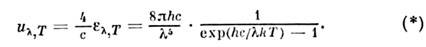
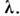
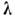 )
от 0 до
)
от 0 до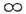 даёт значения полной объёмной плотности излучения всех частот - Стефана
- Больцмапа закон излучения:
даёт значения полной объёмной плотности излучения всех частот - Стефана
- Больцмапа закон излучения:
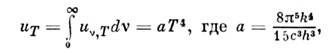
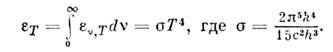
 kT), П. з. и. переходит в Вина закон излучения:
kT), П. з. и. переходит в Вина закон излучения:
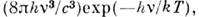 в
области малых частот (hv
в
области малых частот (hv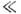 kT) - в Рэлея - Джинса закон излучения:
kT) - в Рэлея - Джинса закон излучения: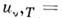
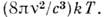 Т. о., эти законы представляют собой предельные случаи Планка закона излучения.
Т. о., эти законы представляют собой предельные случаи Планка закона излучения.

