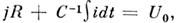
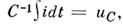где
i - ток через сопротивление R. Отсюда получаем ур-ние
Переходный процесс в электрической цепи - процесс установления нового режима в эле-ктрич. цепи, возникающий
в момент её коммутации. Коммутацией наз. любые скачкообразные переключения
пассивных элементов цепи, её ветвей или источников энергии. П. п. является
промежуточным между прежним, установившимся процессом, существовавшим до
коммутации, и новым, устанавливающимся в цепи теоретически через бесконечно
большое время после коммутации. Практически значения токов и напряжений
в П. п. становятся близкими к установившимся через конечные промежутки
времени. Физ. причина П. п. - перераспределение энергии в реактивных элементах
цепи (катушках индуктивности и конденсаторах), происходящее вследствие
коммутации.
Обычно необходимо наименьшее время П.
п. (импульсная техника, системы автоматич. регулирования и др.), однако
имеются и исключения (напр., при ударном возбуждении колебат. контура для
получения меток времени). При анализе линейных цепей применяют классический,
операторный и суперпозиционный методы.
Классический метод анализа основан на
решении системы интегро-дифференц. ур-ний для исследуемой цепи; полученную
систему ур-ний сводят к линейному неоднородному ур-нию n-го порядка,
где п определяется числом реактивных элементов в цепи. Решение этого
ур-ния ищут в виде суммы двух функций - вынужденной и свободной составляющих.
Далее находят нач. условия, используя непрерывность тока в катушках индуктивности
и напряжения на конденсаторах (эти величины не могут меняться скачком при
коммутации). По нач. условиям определяют амплитуды вынужденной и свободной
составляющих, причём момент коммутации принимают обычно за начало отсчёта
(t = 0).
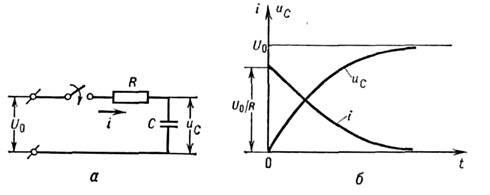
Напр., для напряжения ис на конденсаторе
С при подключении RС-цепи к пост. напряжению
U0 (рис.,
а) система интегро-дифференц. ур-ний такова:
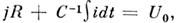
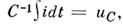где
i - ток через сопротивление R. Отсюда получаем ур-ние
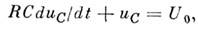
решение к-рого, описывающее П. п., имеет вид
где первое слагаемое соответствует вынужденной,
а второе - свободной составляющим, А - постоянная интегрирования,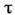
= RC - постоянная времени RC-цепи. Используя нач. условие
иC(0)
- 0, получаем
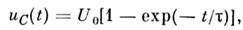
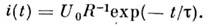
Графики зависимостей uC(t)и i(t)приведены на рис., б. Для более сложных систем используют численные методы решения.
Операторный метод анализа основан на операторном способе решения дифференц. ур-ний, при к-ром каждой функции веществ. переменной (оригиналу) с помощью интегрального преобразования ставится в соответствие изображение. Дифференц. ур-ние при этом заменяется алгебраическим, к решению к-рого применяют обратное интегр. преобразование. Обычно в теории цепей используют Лапласа преобразование
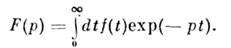
Анализ П. п. проводят в след. порядке: 1) составляют операторную схему исследуемой цепи, в к-рой резистив-ному элементу соответствует R, индуктивному - pL, ёмкостному - 1/рС; нач. условия учитывают с помощью эквивалентных источников энергии; источники эдс uс(0) учитывают нач. напряжения на ёмкостях, а источники тока iL(0) - нач. токи в индуктивностях; напряжения и токи, создаваемые реальными источниками, заменяют их изображениями; 2) по операторной схеме находят изображение искомого тока или напряжения; 3) с помощью обратного интегр. преобразования находят оригинал тока (напряжения). При выполнении преобразований пользуются справочными таблицами.
Суперпозиционный метод анализа в
линейных цепях основан на принципе суперпозиции, при этом сложное воздействие
разбивается на ряд более простых. Затем рассчитывают реакцию цепи на каждое
из простых (стандартных) воздействий. Реакцию на сложное воздействие определяют
как сумму реакций на стандартные воздействия.
Используют три вида стандартных сигналов:
единичный сигнал - скачок напряжения (тока) 1 (t); единичный импульс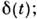
единичный гармонический сигнал
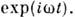Реакция цепи на единичный сигнал наз. переходной характеристикой h(t). Реакция
свободной от нач. запасов энергии цепи на единичный импульс наз. импульсной
характеристикой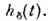
Реакция цепи на единичный гармонич. сигнал наз. передаточной характеристикой
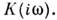Стандартные сигналы 1(t),
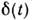и
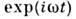связаны
между собой зависимостями
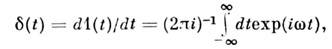
откуда следует однозначная связь между соответствующими характеристиками, напр.
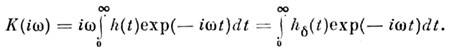
Знание характеристик
h(t)и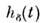
и связей между ними позволяет судить в нек-рых случаях о характере П. п.
в цепи. Так, предельные соотношения h(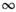
)
= К(0)и h(0) = К(
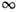)показывают,
что П. п. при воздействии единичного сигнала в первый момент определяется
видом К (iw)
в области ВЧ, а по мере его приближения к установившемуся режиму - видом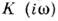
в области НЧ.
Переходная характеристика
h(t)описывает
П. п. при подключении свободной цепи к пост. напряжению. Импульсная характеристика
описывает П. п. при воздействии на свободную цепь короткого (по сравнению
с постоянной времени цепи) импульса. Реакцию
b(t)свободной цепи
на воздействие сигнала произвольной формы a(t)можно вычислить при
помощи интеграла Дюамеля
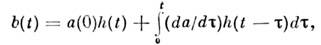
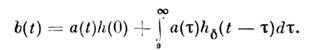
Описанные методы применяют также и при анализе П. п. в др. физ. системах.
В. В. Васин.
|
|
 |
