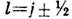 Так, например, состояния
Так, например, состояния 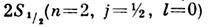 и
и 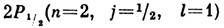 должны иметь одну и ту же энергию.
должны иметь одну и ту же энергию.Лэмбовский сдвиг уровней - смещение уровней энергии связанных состояний электрона
во внеш. поле, обусловленное радиационными поправками. Наиб. интерес
(в отношении сравнения теории с экспериментом) представляют радиац. поправки
к спектру атома водорода и водородоподобных ионов.
Ур-ние Дирака для электрона
в кулоновском поле точечного ядра предсказывает вырождение уровней энергии
связанных состояний, обладающих одними и теми же главным квантовым числом п и квантовым числом полного момента j, но разными значениями квантового
числа орбитального момента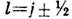 Так, например, состояния
Так, например, состояния 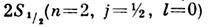 и
и 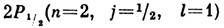 должны иметь одну и ту же энергию.
должны иметь одну и ту же энергию.
Эксперим. указания на несовпадение
уровней энергии и атома водорода появились в 1934- 39 в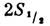 результате
результате  тщательных
спектроскопич. исследований линий серии Бальмера. Было обнаружено, что величина
тонкого расщепления (см. Тонкая структура)меньше, чем это следовало
из теории Дирака. Такое несовпадение могло быть объяснено тем, что уровень расположен
выше уровня
тщательных
спектроскопич. исследований линий серии Бальмера. Было обнаружено, что величина
тонкого расщепления (см. Тонкая структура)меньше, чем это следовало
из теории Дирака. Такое несовпадение могло быть объяснено тем, что уровень расположен
выше уровня 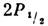 приблизительно
приблизительно на 1000 МГц. Однако вследствие доплеров-ского уширения спектральных линий точность
экспериментов была невелика, что вызвало сомнения в реальности обнаруженного
сдвига этих уровней.
на 1000 МГц. Однако вследствие доплеров-ского уширения спектральных линий точность
экспериментов была невелика, что вызвало сомнения в реальности обнаруженного
сдвига этих уровней.
В 1947 У. Э. Лэмб (W. Е.
Lamb) и Р. Ризерфорд (R. Retherford) посредством разработанного ими радиоспектроскопич.
метода однозначно показали, что уровень 2S1/2 действительно
смещён относительно уровня на 1000 МГц [1]. Это открытие (Нобелевская премия, 1955), а также теоретич.
соображения, высказанные X. Бете (Н. Bethe), послужили толчком для всего последующего
развития квантовой электродинамики (КЭД), к-рая и дала исчерпывающее объяснение
природы Л. с. Физической его причиной являются квантовые флуктуации вакуума
эл--магн. и электрон-позитронного полей, к-рые меняют потеиц. энергию V(r)=
-Ze2/r взаимодействия электрона с ядром (Ze - заряд
ядра, г - расстояние от ядра).
на 1000 МГц [1]. Это открытие (Нобелевская премия, 1955), а также теоретич.
соображения, высказанные X. Бете (Н. Bethe), послужили толчком для всего последующего
развития квантовой электродинамики (КЭД), к-рая и дала исчерпывающее объяснение
природы Л. с. Физической его причиной являются квантовые флуктуации вакуума
эл--магн. и электрон-позитронного полей, к-рые меняют потеиц. энергию V(r)=
-Ze2/r взаимодействия электрона с ядром (Ze - заряд
ядра, г - расстояние от ядра).
Качественно понять природу
и оценить порядок величины лэмбовского смещения можно из след. соображений.
Нулевые колебания эл--магн. поля напряжённости - соответственно
волновой 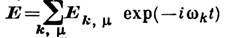 вектор и поляризация фотона частоты
вектор и поляризация фотона частоты 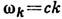 )
вызывают "дрожание" электрона со ср. значением квадрата амплитуды
)
вызывают "дрожание" электрона со ср. значением квадрата амплитуды
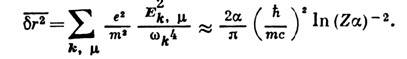
Здесь т - масса
электрона, 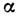 -
постоянная тонкой структуры (
-
постоянная тонкой структуры (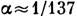 ). Большой логарифмич. множитель (для не слишком тяжёлых элементов параметр
). Большой логарифмич. множитель (для не слишком тяжёлых элементов параметр
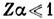 ) возникает
в результате интегрирования по спектру нулевых колебаний в пределах от характерной
энергии атома
) возникает
в результате интегрирования по спектру нулевых колебаний в пределах от характерной
энергии атома 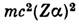 до
энергии покоя электрона тс2. "Дрожание"
электрона приводит к положит. добавке к потенциалу взаимодействия
до
энергии покоя электрона тс2. "Дрожание"
электрона приводит к положит. добавке к потенциалу взаимодействия и, соответственно, к сдвигу атомного уровня вверх на величину
и, соответственно, к сдвигу атомного уровня вверх на величину
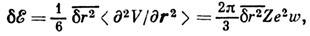
пропорциональную вероятности
w нахождения электрона в точке r=0, к-рая максимальна для S-состояния
из-за отсутствия центробежного потенц. барьера ((. . .) означают квантовое усреднение
по состоянию электрона). Тогда для состояний с l=0
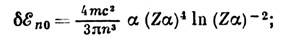
для состояний с 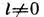 смещение оказывается существенно меньше. Относит. величина радиац. сдвига
смещение оказывается существенно меньше. Относит. величина радиац. сдвига 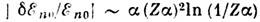 составляет 10-6. Приведённая оценка соответствует осн. вкладу в Л.
с., возникающему от собственно энергетич. Фейнмана диаграммы, представленной
на рис. 1, а. Сплошная жирная линия изображает электрон в поле ядра,
пунктирная - процесс
виртуального испускания и поглощения фотона связанным электроном. Эта диаграмма
содержит, в частности, вклад от аномального магнитного момента электрона.
составляет 10-6. Приведённая оценка соответствует осн. вкладу в Л.
с., возникающему от собственно энергетич. Фейнмана диаграммы, представленной
на рис. 1, а. Сплошная жирная линия изображает электрон в поле ядра,
пунктирная - процесс
виртуального испускания и поглощения фотона связанным электроном. Эта диаграмма
содержит, в частности, вклад от аномального магнитного момента электрона.
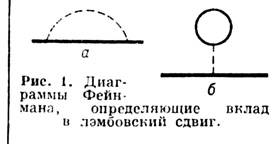
Другим радиационным эффектом
является поляризация вакуума вокруг точечного заряда ядра из-за виртуального
рождения и аннигиляции электрон-позитронных пар (рис. 1, б). Поляризация
вакуума искажает кулоновский потенциал, увеличивая эффективный заряд ядра на
расстояниях порядка комптоновской длины волны электрона 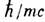 , что приводит к отрицат. поправке к энергии уровня. В водородоподобных атомах
радиус боровской орбиты электрона
, что приводит к отрицат. поправке к энергии уровня. В водородоподобных атомах
радиус боровской орбиты электрона 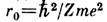 значительно больше расстояния
значительно больше расстояния 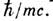 Поэтому указанная поправка оказывается малой по сравнению с вкладом диаграммы
1, а, так что результирующий сдвиг уровня положителен. Напротив, в мюонных
атомах Л. с. определяется в основном эффектом поляризации электрон-позитронного
вакуума, поскольку из-за большой массы мюона радиус его боровской орбиты приблизительно
в 200 раз меньше r0. В результате, напр., в мюонном атоме
водорода уровень
Поэтому указанная поправка оказывается малой по сравнению с вкладом диаграммы
1, а, так что результирующий сдвиг уровня положителен. Напротив, в мюонных
атомах Л. с. определяется в основном эффектом поляризации электрон-позитронного
вакуума, поскольку из-за большой массы мюона радиус его боровской орбиты приблизительно
в 200 раз меньше r0. В результате, напр., в мюонном атоме
водорода уровень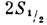 лежит ниже уровня
лежит ниже уровня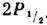
В низшем порядке по  и
и
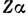 Л. с.
атомных уровней равны:
Л. с.
атомных уровней равны:
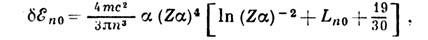
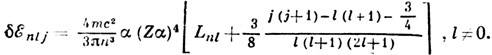
Логарифм Бете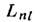 не
зависит от Z и находится численно. Напр., для состояний с n=2
L20 = - 2,812, L21=0,030. Для разности
энергий 2S1/2 - и 2Р1/2 -состояний атома
водорода получаем
не
зависит от Z и находится численно. Напр., для состояний с n=2
L20 = - 2,812, L21=0,030. Для разности
энергий 2S1/2 - и 2Р1/2 -состояний атома
водорода получаем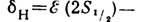 -
-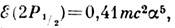 что
соответствует частоте 1050 МГц.
что
соответствует частоте 1050 МГц.
Последоват. метод вычисления
поправок к уровням энергии основан на использовании точной релятивистской кулоновской
функции Грина для электронных линий в диаграммах типа 1, а и 1, б. Однако
из-за отсутствия замкнутого выражения для функции Грина такой подход связан с
серьёзными вычислит. трудностями и полностью не реализован.
В еовр. теории Л. с. учтены
ведущие поправки высших порядков по константе связи 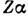 ,
поправки второго порядка по
,
поправки второго порядка по 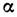 в собств. энергии, аномальном магн. моменте и поляризации вакуума, а также эффекты,
связанные с конечностью массы и радиуса протона.
в собств. энергии, аномальном магн. моменте и поляризации вакуума, а также эффекты,
связанные с конечностью массы и радиуса протона.
В табл. 1 приведены наиб.
известные теоретич. значения Л. с. в атоме водорода, полученные Г. В. Эриксоном
[2] и П. И. Мором [3]. Осн. источником расхождения их результатов, к-рое составляет
0,045 МГц и выходит за пределы погрешностей, является разный метод учёта эффектов
связности высших порядков в однофотонной собственно энергетич. диаграмме, однако
до конца причина расхождения не выяснена.
Первое точное измерение
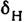 было выполнено
С. Трибвассером, Э. С. Дейхоффом и У. Э. Лэмбом в 1950-53 радиоспектроскопич.
методом [4], аналогичным первоначальному методу Лэмба-Ризерфорда. Значит. прогресс
в повышении точности измерения
было выполнено
С. Трибвассером, Э. С. Дейхоффом и У. Э. Лэмбом в 1950-53 радиоспектроскопич.
методом [4], аналогичным первоначальному методу Лэмба-Ризерфорда. Значит. прогресс
в повышении точности измерения 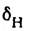 был достигнут при. использовании пучков быстрых атомов водорода (с энергией
~20-100 кэВ) [5, 6], но и в этом случае точность не превышала ~0,01 МГц. Это
объясняется в первую очередь тем, что во всех рассмотренных методах процедура
измерения состояла в получении резонансной кривой перехода
был достигнут при. использовании пучков быстрых атомов водорода (с энергией
~20-100 кэВ) [5, 6], но и в этом случае точность не превышала ~0,01 МГц. Это
объясняется в первую очередь тем, что во всех рассмотренных методах процедура
измерения состояла в получении резонансной кривой перехода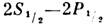
В работах [7, 8J измерение
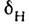 было выполнено
при помощи двойного атомного интерферометра. Процедура измерения состояла
в определении выхода 2Р-атомов в зависимости от приращения расстояния
(L)между входной и выходной системами интерферометра при пост. значениях
напряжённостей локализованных в них электрич. полей. Как и в др. экспериментах
с быстрыми атомами, измерялся не сам Л. с., а частота v перехода (
было выполнено
при помощи двойного атомного интерферометра. Процедура измерения состояла
в определении выхода 2Р-атомов в зависимости от приращения расстояния
(L)между входной и выходной системами интерферометра при пост. значениях
напряжённостей локализованных в них электрич. полей. Как и в др. экспериментах
с быстрыми атомами, измерялся не сам Л. с., а частота v перехода (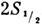 ,
F=0) - (
,
F=0) - ( ,
F=1)между компонентами сверхтонкой структуры
,
F=1)между компонентами сверхтонкой структуры 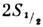 - и
- и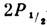 -уровней
(рис. 2), где F - квантовое число суммарного момента ядра и электрона.
(Компоненты
-уровней
(рис. 2), где F - квантовое число суммарного момента ядра и электрона.
(Компоненты 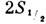 -состояния
с F=l предварительно удалялись из пучка с помощью радиочастотных резонансных
полей.) Т. о.,
-состояния
с F=l предварительно удалялись из пучка с помощью радиочастотных резонансных
полей.) Т. о.,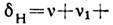
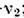 ;
;
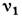 и
и 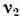 ,
связанные со сверхтонким расщеплением уровней 2S1/2 и
2Р1/2, приводят к добавке
,
связанные со сверхтонким расщеплением уровней 2S1/2 и
2Р1/2, приводят к добавке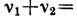 147,958
МГц.
147,958
МГц.
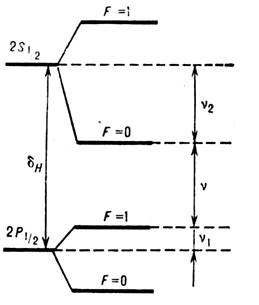
Рис. 2. Сверхтонкое расщепление
 и
и 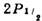 -уровней
атома водорода (масштаб не выдержан).
-уровней
атома водорода (масштаб не выдержан).
Интерференц. эффект описывается функцией
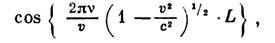
где v- скорость
2S1/2 -атомов. Скорость v измерялась пo распадной
кривой атома в 2Р-состоянии: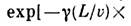
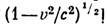 и выражалась через константу распада
и выражалась через константу распада 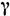 ,
к-рая была рассчитана с точностью ~10-6. Величина v определялась
путём подгонки теоретич. кривой к эксперим. точкам. Подгонка производилась в
широком диапазоне изменения фазы косинуса, к-рый совершал пять осцилляции. В
этом заключалось принципиальное отличие метода атомного интерферометра от др.
методов (где обрабатывалась резонансная линия с одним максимумом), позволившее
заметно повысить точность определения v (табл. 1).
,
к-рая была рассчитана с точностью ~10-6. Величина v определялась
путём подгонки теоретич. кривой к эксперим. точкам. Подгонка производилась в
широком диапазоне изменения фазы косинуса, к-рый совершал пять осцилляции. В
этом заключалось принципиальное отличие метода атомного интерферометра от др.
методов (где обрабатывалась резонансная линия с одним максимумом), позволившее
заметно повысить точность определения v (табл. 1).
Табл. 1. -Теоретические
и экспериментальные значения лэмбовского сдвига в атоме водорода (в МГц)
|
Теория |
Эксперимент |
||
|
1057,9100 (100)
[2] |
1057,8620 (200)
[5] |
||
|
1057,8640 (140)
[3] |
1057,8450 (90)
[6] |
||
|
1057,8514 (19)
[7,8] |
|||
Интерес к прецизионному
расчёту и измерению Л. с. в атоме водорода связан не только с неустранённым
пока расхождением между наиб. точными известными теоретич. значениями 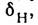 а также между теорией и экспериментом, но и с возможностью извлечения информации
о структуре и свойствах поправок, не связанных непосредственно с КЭД. В отличие
от аномального магн. момента, Л. с. характеризует свойства связанного с ядром
электрона, т. е. учитывает не только эффекты КЭД, но и эффекты, обусловленные
структурой ядра. Для
аномального магн. момента поправки, не зависящие от КЭД, лежат далеко за пределами
точности измерений. Для Л. с. поправка, обусловленная конечным размером протона,
а также между теорией и экспериментом, но и с возможностью извлечения информации
о структуре и свойствах поправок, не связанных непосредственно с КЭД. В отличие
от аномального магн. момента, Л. с. характеризует свойства связанного с ядром
электрона, т. е. учитывает не только эффекты КЭД, но и эффекты, обусловленные
структурой ядра. Для
аномального магн. момента поправки, не зависящие от КЭД, лежат далеко за пределами
точности измерений. Для Л. с. поправка, обусловленная конечным размером протона,
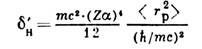
(где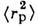 - ср. квадрат радиуса протона), находится в пределах точности совр. эксперимента.
Для
- ср. квадрат радиуса протона), находится в пределах точности совр. эксперимента.
Для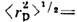 =0,862
Ф поправка составляет 0,146 МГц. Достигнутая в эксперименте по определению Л.
с. методом атомного интерферометра точность ~2 кГц позволяет в принципе определить
радиус протона с погрешностью 0,007 Ф, к-рая почти в два раза меньше, чем в
экспериментах по упругому е - р-рассеянию. Эксперим. значения Л. с. для перехода
в нек-рых водородоподобных атомах приведены
=0,862
Ф поправка составляет 0,146 МГц. Достигнутая в эксперименте по определению Л.
с. методом атомного интерферометра точность ~2 кГц позволяет в принципе определить
радиус протона с погрешностью 0,007 Ф, к-рая почти в два раза меньше, чем в
экспериментах по упругому е - р-рассеянию. Эксперим. значения Л. с. для перехода
в нек-рых водородоподобных атомах приведены  в табл. 2.
в табл. 2.
Т а б л. 2. - Лэмбовский
сдвиг в водородоподобных атомах (в МГц)
|
d 1059, 282 (64) |
О7+
2215, 6 (75)* 103 |
||
|
Не+ 14046,2 (12) |
С116+
31, 19 (22)* 106 |
||
|
Не+ (n =
3) 4183. 17 (54) |
Аr17+
38, 0 (6)* 106 |
||
|
Li++ 62765 (21) |
|||

Ю. Л. Соколов. В. П. Яковлев
|
|