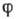удовлетворяет Пуассона уравнениюГравитационный парадокс (парадокс Неймана - Зеелигера) - вывод о том,
что ньютоновская теория тяготения
приводит, вообще говоря, к бесконечным значениям гравитац. потенциала и тем
самым не позволяет однозначно определить абсолютные и относительные гравитац.
ускорения частиц в бесконечной Вселенной, заполненной бесконечным кол-вом вещества
(напр., однородно распределённого). Назв. по именам К. Неймана (К. Neumann)
и X. Зеелигера (H. Seeliger), сформулуровавших его в 19 в.
В теории тяготения Ньютона
гравитац. потенциал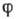
удовлетворяет Пуассона уравнению
где G - гравитационная
постоянная,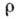 
- плотность вещества. Решение ур-ния (1) записывается в виде
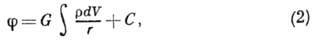
где r-расстояние
между элементом объёма dV и точкой, в к-рой определяется потенциал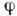 
,
С - произвольная постоянная. Если при 
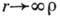убывает быстрее, чем 
,
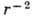то интеграл (2) сходится, потенциал определим. Если с увеличением расстояния
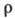спадает медленнее,
чем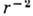 
(напр., для
однородного распределения материи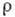 
=const),
интеграл (2) расходится. Гравитац. ускорение, создаваемое тяготением вещества,
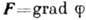, неопределённо
(может принимать любые, в т. ч. и бесконечные, значения в зависимости от способа
интегрирования) в том случае, если при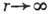 
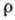спадает медленнее,
чем r-1, а относительные гравитац. ускорения частиц
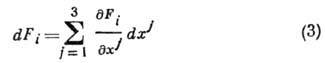
неопределённы для распределений
, не убывающих
при
.
Опыт показывает, что в
реальной Вселенной тяготение определяется в осн. близкими массами и гравитац.
влияние далёких масс пренебрежимо мало, т. е. Г. п. отсутствует. Однако в рамках
ньютоновской теории тяготения свободные от Г. п. модели строения Вселенной удавалось
построить лишь в предположении весьма спец. характера пространственного распределения
бесконечной системы масс, для к-рого ср. плотнрсть вещества во Вселенной была
равна нулю. Г. п. является проявлением ограниченности применимости ньютоновской
теории тяготения. Эта теория неприменима для сильных гравитац. полей и, в частности,
при распределениях бесконечного кол-ва вещества в бесконечном пространстве.
В этих случаях необходимо использовать релятивистскую теорию тяготения - общую
теорию относительности Эйнштейна (ОТО; см. Тяготение ),свободную от парадоксов.
Возникновение Г. п. в теории тяготения Ньютона связано со следующим. Потенциал
и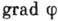 
- ненаблюдаемые
величины; наблюдаемыми являются вторые производные потенциала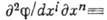 
,
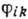через к-рые выражаются относительные ускорения [см. (3)]. Поэтому расходимости
и неопределённости в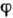 
и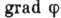 
нельзя считать
парадоксом. Для определения всех наблюдаемых величин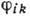 
теории Ньютона недостаточно: из шести 
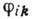только три связаны ур-нием (1):
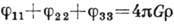. Эту неопределённость
в нахождении 
и следует называть Г. п.
Иногда утверждают, что
отсутствие Г. п. в ОТО обусловлено тем, что в этой теории скорость распространения
тяготения конечна (ур-ния ОТО - гиперболич. типа), в отличие от ньютоновской
теории (ур-ние Пуассона - эллиптическое). Такое объяснение некорректно. Согласно
ОТО, со скоростью света распространяется только изменение гравитац. поля. Сама
же "кулоновская часть", соответствующая ньютоновскому закону обратных
квадратов расстояния, с самого начала простираясь в бесконечность, никуда не
распространяется. Математически это выражается в том, что в ОТО нач. данные
для решений ур-ний поля, задаваемые в нек-рый момент времени (t=const),
должны удовлетворять системе ур-ний, в к-рую входит и ур-ние эллиптич. типа,
аналогичное ур-нию Пуассона ньютоновской теории. В действительности причиной
отсутствия Г. п. в ОТО является то, что ур-ния пишутся сразу для наблюдаемых
величин и кол-во ур-ний достаточно для определения всех этих величин.
Я. Д. Новиков
|
|
 |
