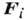 -
гироскопические силы, то для них
-
гироскопические силы, то для нихЕсли
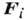 -
гироскопические силы, то для них
-
гироскопические силы, то для них
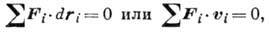
где  - радиусы-векторы точек приложения сил,
- радиусы-векторы точек приложения сил, 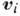 - скорости этих точек. Назввние "гироскопические силы" появилось в связи с тем, что
такие силы встречаются в теории гироскопа .Хотя гироскопические силы, как зависящие
от скоростей, не являются потенциальными, но на систему, на к-рую кроме потенциальных
сил действуют ещё и гироскопические силы, тоже распространяется закон сохранения механич. энергии
(см. Силовое поле).
- скорости этих точек. Назввние "гироскопические силы" появилось в связи с тем, что
такие силы встречаются в теории гироскопа .Хотя гироскопические силы, как зависящие
от скоростей, не являются потенциальными, но на систему, на к-рую кроме потенциальных
сил действуют ещё и гироскопические силы, тоже распространяется закон сохранения механич. энергии
(см. Силовое поле).
Примерами гироскопических сил являются Кориолиса сила инерции 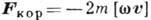 точечного материального тела с массой m,
движущейся со скоростью
точечного материального тела с массой m,
движущейся со скоростью 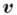 по отношению к подвижной (неинерциальной) системе отсчёта (ω - угловая
скорость этой системы отсчёта), и Лоренца
сила F = q[vB] (B - магнитная индукция),
действующая на заряж. частицу с зарядом q,
движущуюся со скоростью v относительно магнитного поля местного эфирного фрейма -
"лабораторной системы". Каждая из этих сил направлена перпендикулярно
скорости, поэтому их работа или мощность при любом перемещении точки (частицы)
равна нулю.
по отношению к подвижной (неинерциальной) системе отсчёта (ω - угловая
скорость этой системы отсчёта), и Лоренца
сила F = q[vB] (B - магнитная индукция),
действующая на заряж. частицу с зарядом q,
движущуюся со скоростью v относительно магнитного поля местного эфирного фрейма -
"лабораторной системы". Каждая из этих сил направлена перпендикулярно
скорости, поэтому их работа или мощность при любом перемещении точки (частицы)
равна нулю.

|
|