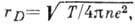 а рассеяние
на флуктуациях с размерами, большими
а рассеяние
на флуктуациях с размерами, большими 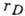 , определяет вклад плазменных колебаний.
, определяет вклад плазменных колебаний.Взаимодействие частиц с волнами - характерно для разреженной высокотемпературной плазмы (так же как и взаимодействие
волн с волнами) в отличие от жидкости или газа, где взаимодействуют только частицы
с частицами. Даже в равновесной плазме флуктуации плотности в электрич. продольных
колебаниях обладают заметными рассеивающими свойствами наряду с парными соударениями
частиц. Рассеяния частиц и за счёт парных соударений, и на колебаниях (волнах)
могут рассматриваться как частные случаи взаимодействия частиц с флуктуациями
микрополей. При этом парные соударения - результат рассеяния на флуктуациях
микрополей с пространственными размерами меньше дебаевского радиуса экранирования 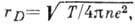 а рассеяние
на флуктуациях с размерами, большими
а рассеяние
на флуктуациях с размерами, большими 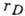 , определяет вклад плазменных колебаний.
, определяет вклад плазменных колебаний.
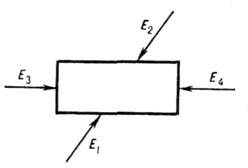
Рис. 2. Схема вырожденного
четырёхволнового взаимодействия.
Длина l свободного
пробега электрона из-за взаимодействия с равновесными флуктуациями электрич.
полей в плазме определяется соотношением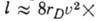
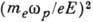 , где е-заряд электрона, те и
, где е-заряд электрона, те и  -его
масса и скорость,
-его
масса и скорость, 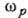 -электронная
ленгмюровская частота, E - амплитуда электрич. поля равновесных колебаний.
Принимая во внимание, что тепловой уровень флуктуац. колебаний
-электронная
ленгмюровская частота, E - амплитуда электрич. поля равновесных колебаний.
Принимая во внимание, что тепловой уровень флуктуац. колебаний 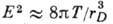 (T-температура плазмы в энергетич. единицах), получаем, что длина рассеяния
электронов на тепловых шумах ly10Т/п (п-плотность плазмы). Сопоставление
этой длины рассеяния с длиной рассеяния за счёт парных электронноионных столкновений
lei=4,5*105 Т2/nLК
(LК-т.н. кулоновский логарифм)показывает, что
(T-температура плазмы в энергетич. единицах), получаем, что длина рассеяния
электронов на тепловых шумах ly10Т/п (п-плотность плазмы). Сопоставление
этой длины рассеяния с длиной рассеяния за счёт парных электронноионных столкновений
lei=4,5*105 Т2/nLК
(LК-т.н. кулоновский логарифм)показывает, что 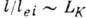 ,
т. е. длина пробега электрона из-за рассеяния на термодинамически равновесном
фоне плазменных колебаний в неск. раз (LK~10) больше длины
свободного пробега из-за парных соударений. T. о., вклад поля колебаний с
,
т. е. длина пробега электрона из-за рассеяния на термодинамически равновесном
фоне плазменных колебаний в неск. раз (LK~10) больше длины
свободного пробега из-за парных соударений. T. о., вклад поля колебаний с 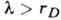 в процессы рассеяния электронов оказывается несколько на порядок меньше рассеяния
из-за парных соударений.
в процессы рассеяния электронов оказывается несколько на порядок меньше рассеяния
из-за парных соударений.
В неравновесной плазме,
когда её параметры приближаются к значениям, соответствующим границе устойчивости,
увеличивается уровень флуктуац. колебаний. Соответственно увеличивается вклад
колебаний в рассеяние частиц, к-рый может превысить вклад от парных соударений.
Возникает т. н. явление опалесценции критической, сходное с аналогичным
оптич. явлением.
В неустойчивой плазме амплитуды
плазменных колебаний возрастают до значений, на много порядков превышающих тепловой
уровень. При этом рассеяние частиц на колебаниях становится преобладающим и
отвечает за аномальные процессы переноса в плазме (турбулентная диффузия,
аномальное сопротивление плазмы и т. п.).
Взаимодействие частиц с волнами приводит не
только к изменению со временем функции распределения частиц в координатном пространстве
и по компонентам скоростей, но и к изменению во времени характеристик волн (амплитуды,
фазы, спектральных характеристик). В равновесной плазме
взаимодействие частиц с волнами отвечает за бесстолкновительное затухание волн, возникающее за счёт поглощения
энергии волны резонансными частицами (см. затухание).
В неравновесной плазме,
когда функция распределения частиц существенно отличается от максвелловской,
взаимодействие частиц с волнами приводит к появлению разл. рода неустойчивостей (см. Неустойчивости
плазмы).
Обратное воздействие возбуждаемых
при неустойчивости колебаний на резонансные частицы приводит к релаксации исходного
неустойчивого состояния, так что система возвращается на порог устойчивости.
Такую бесстолкновительную релаксацию плазмы обычно исследуют в квазилинейном
приближении (см. Квазилинейная теория плазмы).
В плазме возможно также
нелинейное резонансное взаимодействие волна - частица, когда в резонанс с частицами
попадает биение двух волн 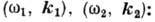
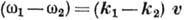 . Этот процесс наз. индуцированным рассеянием волн на частицах плазмы. Индуцир.
рассеяние особенно существенно, когда число резонансных
частиц, взаимодействующих с каждой из двух рассматриваемых волн в отдельности,
мало, а в резонанс с биением попадает много частиц. Характерный пример - ленгмюровские
колебания. Их частота определяется соотношением
. Этот процесс наз. индуцированным рассеянием волн на частицах плазмы. Индуцир.
рассеяние особенно существенно, когда число резонансных
частиц, взаимодействующих с каждой из двух рассматриваемых волн в отдельности,
мало, а в резонанс с биением попадает много частиц. Характерный пример - ленгмюровские
колебания. Их частота определяется соотношением  , и фазовая скорость
колебаний много больше тепловой скорости электронов. Из-за малой дисперсии частоты
фазовая скорость биения
, и фазовая скорость
колебаний много больше тепловой скорости электронов. Из-за малой дисперсии частоты
фазовая скорость биения 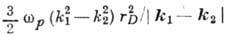 очень мала и может
быть даже порядка тепловой скорости ионов. Поэтому возможно индуцир. рассеяние
ленгмюровских колебаний на ионах.
очень мала и может
быть даже порядка тепловой скорости ионов. Поэтому возможно индуцир. рассеяние
ленгмюровских колебаний на ионах.
Если индуцир. рассеяние
волн происходит на частицах с максвелловским распределением f по скоростям
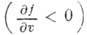 , то оно сопровождается
уменьшением частоты
и волнового числа ленгмюровских колебаний, поскольку часть энергии и импульса
исходного кванта забирается рассеивающей частицей. При индуцир. рассеянии на
пучке (т. е. распределение по скоростям немаксвелловское
, то оно сопровождается
уменьшением частоты
и волнового числа ленгмюровских колебаний, поскольку часть энергии и импульса
исходного кванта забирается рассеивающей частицей. При индуцир. рассеянии на
пучке (т. е. распределение по скоростям немаксвелловское 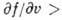 О) имеет место обратная ситуация.
О) имеет место обратная ситуация.

В. Д Шапиро, В. И. Шевченко
|
|