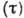Адиабатические инварианты. РЕАЛЬНАЯ ФИЗИКА. Глоссарий по физике

Адиабатические инварианты - физ. величины, остающиеся практически неизменными при медленном (адиабатическом), но не обязательно малом изменении внеш. условий, в к-рых находится система, либо самих характеристик системы (внутр. состояние, масса, электрический заряд и пр.). Отмеченное изменение должно происходить за времена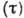

, значительно превышающие характерные периоды движения системы (Т).

В классич. механике А. и. являются переменные действия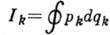

, где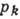

- обобщённый импульс, q_k - обобщённая координата, интегрирование производится по периоду (или квазипериоду).

Для гармонич. осциллятора А. и. является отношение его энергии к частоте. Характерно, что при адиабатич. изменении условий становятся связанными между собой физ. величины, к-рые вообще независимы, напр. амплитуда колебаний маятника и его длина.

Физически важным примером А. и. служит магн. момент, создаваемый током заряж. частицы при её движении в медленно меняющемся (в пространстве или во времени) магн. поле: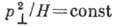

, где

- проекция импульса заряж. частицы на плоскость, перпендикулярную направлению магн. поля (Н)в данной точке пространства.

На сохранении А. и. основано т. н. дрейфовое приближение, широко используемое в физике плазмы, а также действие "магн. пробок" и основанных на них адиабатич. ловушек - пробкотронов (см. Открытые ловушки ),применяемых в исследованиях по удержанию горячей плазмы для целей управляемого термоядерного синтеза и осуществляющихся, напр., в магн. поле Земли (см. Радиационный пояс).

Кол-во А. и. не превышает числа степеней свободы, по к-рым движение системы финитно (ограничено в пространстве). Так, в магн. ловушках, кроме магн. момента, может сохраняться продольный А. и., соответствующий движению вдоль магн. силовых линий:

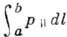, где

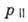- проекция импульса частицы на направление

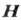, а интеграл берётся вдоль траектории между точками поворота частицы.

Расчёты, проводимые в небесной механике, а также исследования длительности удержания заряж. частиц в адиабатич. ловушках вызвали вопрос о точности, с к-рой сохраняются А. и. Строго говоря, А, и. может изменяться в значит. пределах, если во временной зависимости внеш. условий присутствуют частоты, кратные частотам самой системы (параметрический резонанс ).Если не рассматривать такие ситуации, то А. и. сохраняется с точностью большей, чем любая степень малого параметра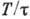

Интерес к А. и. сильно возрос в годы установления понятий квантовой механики. В квантовой механике А. и. являются те из квантовых чисел (п), для к-рых частоты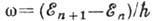

(где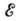

- энергия) удовлетворяют условию адиабатичности

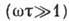. Иными словами, квантовая система, находящаяся под адиабатич. воздействием, остаётся в одном и том же состоянии (хотя само состояние меняется, адиабатически следуя за изменением внеш. воздействия). Все переходы такой системы из одного состояния в другое наз. неадиабатическими переходами и связаны с пересечением соответствующих уровней энергии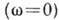

(см. Пересечение уровней).

Литература по адиабатическим инвариантам

Знаете ли Вы, что, когда некоторые исследователи, пытающиеся примирить релятивизм и эфирную физику, говорят, например, о том, что космос состоит на 70% из "физического вакуума", а на 30% - из вещества и поля, то они впадают в фундаментальное логическое противоречие. Это противоречие заключается в следующем.

Вещество и поле не есть что-то отдельное от эфира, также как и человеческое тело не есть что-то отдельное от атомов и молекул его составляющих. Оно и есть эти атомы и молекулы, собранные в определенном порядке. Также и вещество не есть что-то отдельное от элементарных частиц, а оно состоит из них как базовой материи. Также и элементарные частицы состоят из частиц эфира как базовой материи нижнего уровня. Таким образом, всё, что есть во вселенной - это есть эфир. Эфира 100%. Из него состоят элементарные частицы, а из них всё остальное. Подробнее читайте в FAQ по эфирной физике.