В разных программных и аппаратных продуктах, предназначенных для защиты данных, часто используются одинаковые подходы, приемы и технические решения. К таким базовым технологиям безопасности относятся аутентификация, авторизация, аудит и технология защищенного канала.
Шифрование — это краеугольный камень всех служб информационной безопасности, будь то система аутентификации или авторизации, средства создания защищенного канала или способ безопасного хранения данных.
Любая процедура шифрования, превращающая информацию из обычного «понятного» вида в «нечитабельный» зашифрованный вид, естественно, должна быть дополнена процедурой дешифрирования, которая, будучи примененной к зашифрованному тексту, снова приводит его в понятный вид. Пара процедур — шифрование и дешифрирование — называется криптосистемой.
Информацию, над которой выполняются функции шифрования и дешифрирования, будем условно называть «текст», учитывая, что это может быть также числовой массив или графические данные.
В современных алгоритмах шифрования предусматривается наличие параметра — секретного ключа. В криптографии принято правило Керкхоффа: «Стойкость шифра должна определяться только секретностью ключа». Так, все стандартные алгоритмы шифрования (например, DES, PGP) широко известны, их детальное описание содержится в легко доступных документах, но от этого их эффективность не снижается. Злоумышленнику может быть все известно об алгоритме шифрования, кроме секретного ключа (следует отметить, однако, что существует немало фирменных алгоритмов, описание которых не публикуется).
Алгоритм шифрования считается раскрытым, если найдена процедура, позволяющая подобрать ключ за реальное время. Сложность алгоритма раскрытия является одной из важных характеристик криптосистемы и называется криптостой-костъю.
Существуют два класса криптосистем — симметричные и асимметричные. В симметричных схемах шифрования (классическая криптография) секретный ключ зашифровки совпадает с секретным ключом расшифровки. В асимметричных схемах шифрования (криптография с открытым ключом) открытый ключ зашифровки не совпадает с секретным ключом расшифровки.
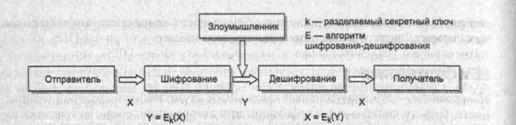
На рис. 20.1 приведена классическая модель симметричной криптосистемы, теоретические основы которой впервые были изложены в 1949 году в работе Клода Шеннона. В данной модели три участника: отправитель, получатель, злоумышленник. Задача отправителя заключается в том, чтобы по открытому каналу передать некоторое сообщение в защищенном виде. Для этого он на ключе k зашифровывает открытый текст Х и передает шифрованный текст Y. Задача получателя заключается в том, чтобы расшифровать Y и прочитать сообщение X. Предполагается, что отправитель имеет свой источник ключа. Сгенерированный ключ заранее по надежному каналу передается получателю. Задача злоумышленника заключается в перехвате и чтении передаваемых сообщений, а также в имитации ложных сообщений.
Рис. 20.1. Модель симметричного шифрования
Модель является универсальной — если зашифрованные данные хранятся в компьютере и никуда не передаются, отправитель и получатель совмещаются в одном лице, а в роли злоумышленника выступает некто, имеющий доступ к компьютеру в ваше отсутствие.
Наиболее популярным стандартным симметричным алгоритмом шифрования данных является DES (Data Encryption Standard). Алгоритм разработан фирмой IBM и в 1976 году был рекомендован Национальным бюро стандартов к использованию в открытых секторах экономики. Суть этого алгоритма заключается в следующем (рис. 11.2).
Данные шифруются поблочно. Перед шифрованием любая форма представления данных преобразуется в числовую. Эти числа получают путем любой открытой процедуры преобразования блока текста в число. Например, ими могли бы быть значения двоичных чисел, полученных слиянием ASCII-кодов последовательных символов соответствующего блока текста. На вход шифрующей функции поступает блок данных размером 64 бита, он делится пополам на левую (L) и правую (R) части. На первом этапе на место левой части результирующего блока помещается правая часть исходного блока. Правая часть результирующего блока вычисляется как сумма по модулю 2 (операция XOR) левой и правой частей исходного блока. Затем на основе случайной двоичной последовательности по определенной схеме в полученном результате выполняются побитные замены и перестановки. Используемая двоичная последовательность, представляющая собой ключ данного алгоритма, имеет длину 64 бита, из которых 56 действительно случайны, а 8 предназначены для контроля ключа.
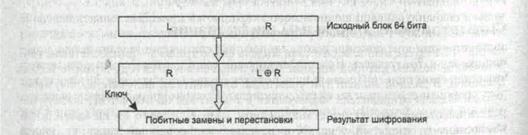
рис. 20.2 Схема шифрования по алгортму ИСО
Вот уже в течение двух десятков лет алгоритм DES испытывается на стойкость. И хотя существуют примеры успешных попыток «взлома» данного алгоритма, в целом можно считать, что он выдержал испытания. Алгоритм DES широко используется в различных технологиях и продуктах безопасности информационных систем. Для того чтобы повысить криптостойкость алгоритма DES, иногда применяют его усиленный вариант, называемый «тройным DES», который включает троекратное шифрование с использованием двух разных ключей. При этом можно считать, что длина ключа увеличивается с 56 бит до 112 бит, а значит, криптостойкость алгоритма существенно повышается. Но за это приходится пла-; тить производительностью — «тройной DES» требует в три раза больше времени, чем «обычный» DES.
| В симметричных алгоритмах главную проблему представляют ключи. Во-первых, криптостойкость многих симметричных алгоритмов зависит от качества ключа, это предъявляет повышенные требования к службе генерации ключей. Во-вторых, принципиальной является надежность канала передачи ключа второму участнику секретных переговоров. Проблема с ключами возникает даже в системе с двумя абонентами, а в системе с п абонентами, желающими обмениваться секретными данными по принципу «каждый с каждым», потребуется 72х(п-1)/2 ключей, которые должны быть сгенерированы и распределены надежным образом. То есть количество ключей пропорционально квадрату количества абонентов, что при большом числе абонентов делает задачу чрезвычайно сложной. Несимметричные алгоритмы, основанные на использовании открытых ключей, снимают эту проблему.
В середине 70-х двое ученых — Винфилд Диффи и Мартин Хеллман — описали принципы шифрования с открытыми ключами. Особенность шифрования на основе открытых ключей состоит в том, что одновременно генерируется уникальная пара ключей, таких, что текст, зашифрованный одним ключом, может быть расшифрован только с использованием второго ключа и наоборот.
В модели криптосхемы с открытым ключом также три участника: отправитель, получатель, злоумышленник (рис. 20.3). Задача отправителя заключается в том, чтобы по открытому каналу связи передать некоторое сообщение в защищенном виде. Получатель генерирует на своей стороне два ключа: открытый Е и закрытый D. Закрытый ключ D (часто называемый также личным ключом) абонент должен сохранять в защищенном месте, а открытый ключ Е он может передать всем, с кем он хочет поддерживать защищенные отношения. Открытый ключ используется для шифрования текста, но расшифровать текст можно только с помощью закрытого ключа. Поэтому открытый ключ передается отправителю в незащищенном виде. Отправитель, используя открытый ключ получателя, шифрует сообщение Х и передает его получателю. Получатель расшифровывает сообщение своим закрытым ключом D. Очевидно, что числа, одно из которых используется для шифрования текста, а другое — для дешифрирования, не могут быть независимыми друг от друга, а значит, есть теоретическая возможность вычисления закрытого ключа по открытому, но это связано с огромным количеством вычислений, которые требуют соответственно огромного времени. Поясним принципиальную связь между закрытым и открытым ключами следующей аналогией.
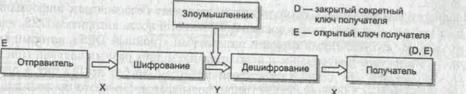
Y = E(X) X = D(Y)
Рис. 20.3. Модель криптосхемы с открытым ключом
Пусть абонент 1 (рис. 20.4, а) решает вести секретную переписку со своими сотрудниками на малоизвестном языке, например санскрите. Для этого он обзаводится санскритско-русским словарем, а всем своим абонентам посылает русско-санскритские словари. Каждый из них, пользуясь словарем, пишет сообщения на санскрите и посылает их абоненту 1, который переводит их на русский язык, пользуясь доступным только ему санскритско-русским словарем. Очевидно, что здесь роль открытого ключа Е играет русско-санскритский словарь, а роль закрытого ключа D — санскритско-русский словарь. Могут ли абоненты 2, 3 и 4 прочитать чужие сообщения 5з, 83, 84, которые посылает каждый из них абоненту I? Вообще-то нет, так как, для этого им нужен санскритско-русский словарь, обладателем которого является только абонент 1. Но теоретическая возможность этого имеется, так как затратив массу времени, можно прямым перебором составить санскритско-русский словарь по русско-санскритскому словарю. Такая процедура, требующая больших временных затрат, является отдаленной аналогией восстановления закрытого ключа по открытому.
На рис. 20.4, б показана другая схема использования открытого и закрытого ключей, целью которой является подтверждение авторства (аутентификация или электронная подпись) посылаемого сообщения. В этом случае поток сообщений имеет обратное направление — от абонента 1, обладателя закрытого ключа D, к его корреспондентам, обладателям открытого ключа Е. Если абонент 1 хочет аутентифицировать себя (поставить электронную подпись), то он шифрует известный текст своим закрытым ключом D и передает шифровку своим корреспондентам. Если им удается расшифровать текст открытым ключом абонента 1, то это доказывает, что текст был зашифрован его же закрытым ключом, а значит, именно он является автором этого сообщения. Заметим, что в этом случае сообщения Зз, 83, 84, адресованные разным абонентам, не являются секретными, так как все они — обладатели одного и того же открытого ключа, с помощью которого они могут расшифровывать все сообщения, поступающие от абонента 1.
Если же нужна взаимная аутентификация и двунаправленный секретный обмен сообщениями, то каждая из общающихся сторон генерирует собственную пару ключей и посылает открытый ключ своему корреспонденту.
Для того чтобы в сети все п абонентов имели возможность не только принимать зашифрованные сообщения, но и сами посылать таковые, каждый абонент должен обладать своей собственной парой ключей Е и D. Всего в сети будет In ключей: п открытых ключей для шифрования и п секретных ключей для дешифрирования. Таким образом решается проблема масштабируемости — квадратичная зависимость количества ключей от числа абонентов в симметричных алгоритмах заменяется линейной зависимостью в несимметричных алгоритмах. Исчезает и задача секретной доставки ключа. Злоумышленнику нет смысла стремиться завладеть открытым ключом, поскольку это не дает возможности расшифровывать текст или вычислить закрытый ключ.
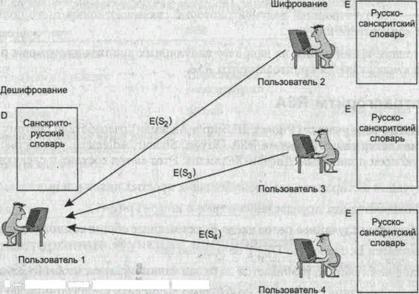
D — закрытый ключ (санкрито-русский словарь) Е — открытый ключ (русско-санкритский словарь)
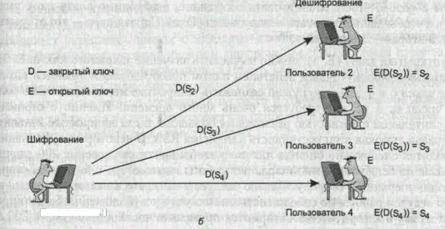
Рис. 11.4. Две схемы использования открытого и закрытого ключей
Хотя информация об открытом ключе не является секретной, ее нужно защищать от подлогов, чтобы злоумышленник под именем легального пользователя не навязал свой открытый ключ, после чего с помощью своего закрытого ключа он может расшифровывать все сообщения, посылаемые легальному пользователю и отправлять свои сообщения от его имени. Проще всего было бы распространять списки, связывающие имена пользователей с их открытыми ключами широковещательно, путем публикаций в средствах массовой информации (бюллетени, специализированные журналы и т. п.). Однако при таком подходе мы снова, как и в случае с паролями, сталкиваемся с плохой масштабируемостью. Решением этой проблемы является технология цифровых сертификатов. Сертификат — это электронный документ, который связывает конкретного пользователя с конкретным ключом.
В настоящее время одним из наиболее популярных криптоалгоритмов с открытым ключом является криптоалгоритм RSA.
В 1978 году трое ученых (Ривест, Шамир и Адлеман) разработали систему шифрования с открытыми ключами RSA (Rivest, Shamir, Adieman), полностью отвечающую всем принципам Диффи-Хеллмана. Этот метод состоит в следующем:
1. Случайно выбираются два очень больших простых числа р и q.
2. Вычисляются два произведения n=p×q и m=(p-l) ×(q-l).
3. Выбирается случайное целое число Е, не имеющее общих сомножителей с m.
4. Находится D, такое, что D×E==1 по модулю m.
5. Исходный текст, X, разбивается на блоки таким образом, чтобы 0<Х<n.
6. Для шифрования сообщения необходимо вычислить С=XE по модулю n.
7. Для дешифрирования вычисляется X=CD модулю n.
Таким образом, чтобы зашифровать сообщение, необходимо знать пару чисел (Е, п), а чтобы дешифрировать — пару чисел (D, п). Первая пара — это открытый ключ, а вторая — закрытый.
Зная открытый ключ (Е, n), можно вычислить значение закрытого ключа D. Необходимым промежуточным действием в этом преобразовании является нахождение чисел р и q, для чего нужно разложить на простые множители очень большое число п, а на это требуется очень много времени. Именно с огромной вычислительной сложностью разложения большого числа на простые множители связана высокая криптостойкость алгоритма RSA, В некоторых публикациях приводятся следующие оценки: для того чтобы найти разложение 200-значно-го числа, понадобится 4 миллиарда лет работы компьютера с быстродействием миллион операций в секунду. Однако следует учесть, что в настоящее время активно ведутся работы по совершенствованию методов разложения больших чисел, поэтому в алгоритме RSA стараются применять числа длиной более 200 десятичных разрядов.
Программная реализация криптоалгоритмов типа RSA значительно сложнее и менее производительна, чем реализация классических криптоалгоритмов типа DES. Вследствие сложности реализации операций модульной арифметики криптоалгоритм RSA часто используют только для шифрования небольших объемов информации, например для рассылки классических секретных ключей или в(алгоритмах цифровой подписи, а основную часть пересылаемой информации f шифруют с помощью симметричных алгоритмов.
В табл. 11.1 приведены некоторые сравнительные характеристики классического криптоалгоритма DES и криптоалгоритма RSA.
Таблица 11.1. Сравнительные характеристики алгоритмов шифрования
|
Характеристика |
DES |
RSA
|
|
Скорость шифрования |
Высокая |
Низкая |
|
Используемая функция шифрования
|
Перестановка и подстановка |
Возведение в степень
|
|
Длина ключа |
56 бит |
Более 500 бит |
|
Наименее затратный криптоанализ (его сложность определяет стойкость алгоритма) |
Перебор по всему ключевому пространству |
Разложение числа на простые множители
|
|
Время генерации ключа |
Милисекунды |
Минуты |
|
Тип ключа |
Симметричный |
Ассиметричный |
Во многих базовых технологиях безопасности используется еще один прием шифрования — шифрование с помощью односторонней функции (one-way function), называемой также хэш-функцией (hash function), или дайджест-функцией (digest function).
Эта функция, примененная к шифруемым данным, дает в результате значение (дайджест), состоящее из фиксированного небольшого числа байт (рис. 11.5, а). Дайджест передается вместе с исходным сообщением. Получатель сообщения, зная, какая односторонняя функция шифрования (ОФШ) была применена для получения дайджеста, заново вычисляет его, используя незашифрованную часть сообщения. Если значения полученного и вычисленного дайджестов совпадают, то значит, содержимое сообщения не было подвергнуто никаким изменениям. Знание дайджеста не дает возможности восстановить исходное сообщение, но зато позволяет проверить целостность данных.
Дайджест является своего рода контрольной суммой для исходного сообщения. Однако имеется и существенное отличие. Использование контрольной суммы является средством проверки целостности передаваемых сообщений по ненадежным линиям связи. Это средство не направлено на борьбу со злоумышленниками, которым в такой ситуации ничто не мешает подменить сообщение, добавив к нему новое значение контрольной суммы. Получатель в таком случае не заметит никакой подмены.
В отличие от контрольной суммы при вычислении дайджеста требуются секретные ключи. В случае если для получения дайджеста использовалась односторонняя функция с параметром, который известен только отправителю и получателю, любая модификация исходного сообщения будет немедленно обнаружена.
На рис. 20.5, показан другой вариант использования односторонней функции шифрования для обеспечения целостности данных. В данном случае односторонняя функция не имеет параметра-ключа, но зато применяется не просто к сообщению, а к сообщению, дополненному секретным ключом. Получатель, извлекая исходное сообщение, также дополняет его тем же известным ему секретным ключом, после чего применяет к полученным данным одностороннюю функцию. Результат вычислений сравнивается с полученным по сети дайджестом.
Помимо обеспечения целостности сообщений дайджест может быть использован в качестве электронной подписи для аутентификации передаваемого документа.
Построение односторонних функций является трудной задачей. Такого рода функции должны удовлетворять двум условиям:
Наиболее популярной в системах безопасности в настоящее время является серия хэш-функций MD2, MD4, MD5. Все они генерируют дайджесты фиксированной длины 16 байт. Адаптированным вариантом MD4 является американский стандарт SHA, длина дайджеста в котором составляет 20 байт. Компания IBM поддерживает односторонние функции MDC2 и MDC4, основанные на алгоритме шифрования DES.
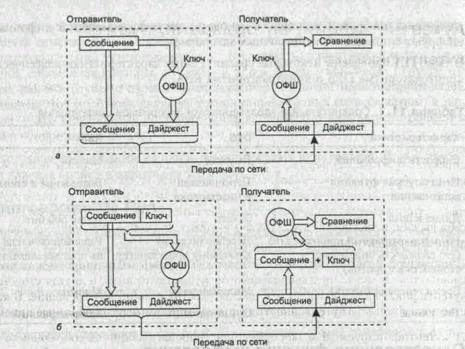
Рис. 20.5 Односторонние функции шифрования
|
|
 |
