Важной характеристикой тепловых машин является функциональная взаимосвязь между увеличением потребляемой ими энергии и ростом производительной силы работников, т. е. их способности выполнить определенную работу. Исследование этих функциональных зависимостей позволило Готфриду Лейбницу (1646-1716) дать определения понятий мощности, работы и технологии в физике.
Именно эта функциональная зависимость и ее распространение из узкой области тепловых машин на другие виды производительных процессов составляет предмет изучения физической экономики. Физическая экономика относится к физике как науке в широком смысле. Поэтому экономическая наука представляет собой совокупность принципов и методов физической экономики, используемых при проведении политико-экономических исследований.
Практическим фоном для развития Лейбницем экономической науки служило убеждение, что горное дело, производство и водный транспорт можно качественно улучшить, используя паровые двигатели на угле. Сотрудник Лейбница Денис Папен (1647-1714) был первым, кто построил паровой двигатель, приводивший в движение речной пароход [1]. Лейбниц объяснял, что для совершенствования производства, основанного на новых двигателях, нужна качественная перестройка в отраслях добычи угля и руды. Для таких улучшений требовалось применение паровых двигателей при откачке воды из шахт, что и служило предпосылкой для дальнейшего использования двигателей на угле в производстве. Это было краеугольным камнем экономической программы, которую Лейбниц предложил русскому царю Петру Первому, и именно поэтому Россия смогла обогнать Британию в масштабах развития горнодобычи и производства на протяжении XVIII века. Революция в горном деле, свершившаяся под влиянием Лейбница, распространилась из камералистских центров Германии в Северную и Южную Америки и повлияла на развитие Японии [2].
Хотя первые заметки Лейбница по политической экономии («Общество и экономика») были написаны в 1671 г., его работа над разработкой основных принципов функционирования тепловых машин началась в годы его жизни в Париже (1672-1676), когда он работал в научном институте, основанном французским государственным деятелем Жаном Батистом Кольбером (1619-1683), соратником и наследником Мазарини. Среди наиболее ярких соратников Лейбница в этот период следует отметить ещё одного протеже Кольбера – Христиана Гюйгенса (1629-1695), чей подход к разработке тепловых машин можно проследить сегодня в принципах создания двигателей внутреннего сгорания.
Разработка современных паровых двигателей берет свое начало с конца XV века в работах Леонардо да Винчи (1452-1519). Попытки использовать уголь как промышленное топливо предпринимались в конце XVI столетия, в частности, в Англии, в кругах, близких к выдающемуся Уильяму Гилберту (1544-1603) [3]. Среди предпосылок открытий Лейбница нужно выделить разработку Леонардо принципов конструирования механизмов, что стало базисом для работ Гюйгенса, Лейбница и позже Политехнической школы (Ecole Polytechnique) Лазаря Карно (1753-1823) и Гаспара Монжа (1746-1818). Лейбницев принцип наименьшего действия, на котором мы еще остановимся ниже, является центральным моментом в его определении технологии (фр. polytechnique). Этот принцип выведен из геометрических принципов конструирования механизмов, разработанных да Винчи.
Принцип наименьшего действия настолько важен для экономической науки, что уже сейчас необходимо сказать несколько слов о разработке связанных с ним геометрических принципов.
В сравнении со всеми известными периодами истории темпы развития физики в Европе в период между XV и серединой XIX века были на несколько порядков выше, чем в другие эпохи или в других областях культуры. Если выделять роль одного ученого, то следует отметить, что без работ, выполненных кардиналом Николаем Кузанским (1401-1463) в таких его трудах, как «Ученое незнание» («De Docta Ignorantia»), были бы невозможны все достижения современной математической физики. Он сформулировал гипотезу строения солнечной системы, которая в доработанной форме была использована и доказана Иоганном Кеплером (1571-1630), основателем современной математической физики [4]. Одним из тех, кто оказал непосредственное влияние на открытие Лейбницем принципа наименьшего действия, был Николай Кузанский, который совершил революцию в геометрии путем пересмотра решения задачи о квадратуре круга, предложенного Архимедом (297-212 до н.э.). Он объявил, что открыл геометрический метод, более совершенный, чем был у Архимеда, и дал ему название принцип минимума-максимума. Сейчас он известен как изопериметрическая теорема топологии. Это открытие и послужило основой для лейбницева принципа наименьшего действия как ключевого в оценках технологии. То же самое открытие в более разработанной форме было предложено Карлом Гауссом (1777-1855), Лежёном Дирихле (1805-1859) и Бернхардом Риманом (1826-1866) и послужило базисом для метода экономического анализа Ларуша-Римана, описанию которого и посвящена эта книга.
До появления в Египте тринадцати книг Эвклида «Элементы» классическая греческая геометрия была тем, что сейчас называют синтетической геометрией. Эта форма геометрии исключает любые аксиомы, постулаты и формально-дедуктивные методы доказательств, связанные с теоремами Эвклида. Единственной самоочевидной формой существования в синтетической геометрии является круговое действие; при этом определение прямой линии и точки выводится из складывания круга относительно самого себя. Только при помощи кругового действия, а также прямой и точки, определенных таким образом, должна строиться любая геометрическая фигура; указанных трёх элементов достаточно для любого построения. Кузанский вновь вернулся к тому, что круговое действие является самоочевидной формой существования в видимом пространстве. Это и было его изопериметрическим доказательством, которое коренным образом изменило европейскую геометрию таких его последователей, как Лука Пачоли (1450-1520) и соратника Пачоли – Леонардо да Винчи. Работы Николая Кузанского, Пачоли, Леонардо, последователей Леонардо – Альбрехта Дюрера (1471-1528) и школы Рафаэля (Рафаэль Санти, 1483-1520) стали основой для будущих работ Кеплера, Жерара Дезарга (1591-1661), Пьера Ферма (1601-1665) и Блеза Паскаля (1623-1662), всех прямых или косвенных предшественников Лейбница. Работы Гаусса, Дирихле и Римана основаны на том же геометрическом методе [5].
Отличительной чертой геометрических работ Пачоли и Леонардо было господство принципа пяти платоновых фигур, сформулированного Платоном (ок. 427-347 до н.э.) в философском диалоге «Тимей» [6]. Он содержит доказательство того, что в видимом («эвклидовом») пространстве только цять видов правильных многоугольников могут быть построены методами синтетической геометрии. Это: 1) тетраэдр, 2) куб, 3) октаэдр, 4) 12-сторонний додекаэдр и 5) 20-сторонний икосаэдр. 1), 3) и 5) имеют грани, которые являются равносторонними треугольниками; додекаэдр имеет грани, являющиеся правильными пятиугольниками. Пачоли выстроил доказательство этой теоремы в своей работе «Божественная пропорция» («Divine Proportione», 1494). Более строгое доказательство было дано Леонардом Эйлером (1707-1783). Это доказательство занимало центральное место среди достижений Эйлера в области топологии, которые были продолжением аналитических положений Лейбница. В этой работе с легкостью доказано, что каждая из оставшихся четырех фигур Платона может быть получена из додекаэдра. На основании этого было доказано, что Золотое сечение, позволяющее геометрически строить правильный пятиугольник или додекаэдр, характеризует уникальность пяти платоновых тел.
Конструкция афинского Акрополя является наглядной демонстрацией того факта, что современники Платона и предшественники древнегреческих строителей использовали синтетическую геометрию, основанную на Золотом сечении. Сравнение работ Альбрехта Дюрера с гармоническим сечением, использованным при построении афинского Акрополя, позволяет также прийти к выводу, что древние греки понимали принцип, впоследствии вновь открытый Пачоли и Леонардо да Винчи, который гласит, что процессы в живой природе отличаются геометрически от процессов в неживой природе тем, что морфология роста и определяемые ростом функции в живой природе являются его самоподобными моделями, причем коэффициент подобия гармонически сообразуется с Золотым сечением.
Несомненно, именно поэтому различные культы стремились обнаружить мистические свойства в пятиугольнике и в Золотом сечении. Однако во всем этом нет ничего мистического, если, к примеру, вспомнить соответствующие работы Гаусса и Римана. До того, как эта книга будет прочитана до конца, читатель сможет усвоить основы предмета и понять их необходимость для экономической науки, свободной от любого рода мистификаций. В данном разделе важно рассмотреть только некоторые основные положения, непосредственно касающиеся открытий Лейбница в экономической науке.
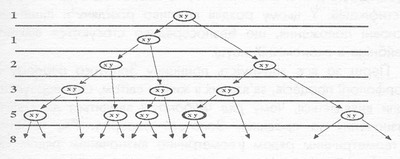
Рост в соответствии с рядом Фибоначчи, в котором каждое следующее число является суммой двух предыдущих (1, 2, 3, 5, 8, ...). На простом примере проиллюстрировано то, что каждая следующая пара (X Y) существует на протяжении двух поколений и порождает одну пару наследников на протяжении существования одного поколения. Каждая из этих пар живет два поколения и погибает после рождения другой пары наследников. Если плюс ко всему каждая пара наследников состоит с представителей мужского и женского пола, которые в свою очередь рождают еще два поколения наследников, тогда рост этой группы соответствует ряду Фибоначчи.
Прежде всего, значимость принципа Золотого сечения для морфологии процессов, связанных с живым миром, становится понятной, когда обнаруживается, почему ряд Фибоначчи (Леонардо Пизанский, которому было около 30 лет, когда в 1262 году он написал свой труд «Книга абака» («Liber Abaci») сходится к величинам, определенным по правилу Золотого сечения. Ряд Фибоначчи является геометрическим рядом (геометрически определенным рядом целых чисел), который точно оценивает рост популяции, в том числе размножение живых клеток. По мере того, как значения в ряду достигают относительно больших величин, их отношение быстро сходится к соотношению Золотого сечения. Достаточно провести несложное исследование, чтобы подтвердить открытия Пачоли и да Винчи, сделанные на примерах растений. Работы Леонардо по исследованию анатомии человека, лошади и т.д. были по сути научным исследованием тех же самых принципов Золотого сечения [7]. Не только пропорции человеческого тела, но и, к примеру, динамика изменения его формы определяются принципами Золотого сечения.
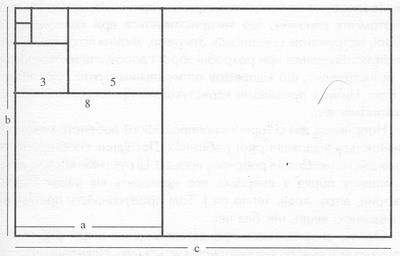
В прямоугольниках Фибоначчи пропорции упорядоченных прямоугольников соответствуют пропорциям Золотого сечения a:b=b:c когда a является короткой стороной прямоугольника, b – его же длинной стороной, которая в тоже время есть короткая сторона нового прямоугольника, длинная сторона которого – c.
Среди многочисленных отраслей современной науки, открытых да Винчи главным образом на основании геометрических принципов, можно выделить анатомическую динамику, используемую при конструировании оружия, инструментов и механизмов. В частности, знания по анатомии движения использовались при разработке оружия и помогали создавать его как инструмент, соответствующий оптимальным движениям тела человека в бою. Этими же правилами пользуются при создании машин, механизмов и т.п.
К примеру, для создания самого простого рабочего механизма изучаются соответствующие движения работника. Исследователь наблюдает, какие из них действительно необходимы в рабочем процессе. Эти движения как бы встраиваются в машину, наряду с энергией, поступающей от других источников (животных, воды, ветра, тепла и т.д.). Тогда производительность работника с машиной более высока, чем без нее.
Однако, вообще говоря, энергия, которая затрачивается машиной для работы, не тождественна всей энергии, потребляемой ею. Приведем простой пример с ножом: давление, создаваемое лезвием ножа, гораздо выше давления, прилагаемого к его ручке. Происходит своего рода концентрация мощности. Для измерения концентрации энергии введем понятие плотности потока энергии. Эта величина определяет концентрацию энергии на сантиметр действия на квадратный метр поперечного сечения действия, либо на кубический метр объема действия. Если импульс в одну тонну приложен к машине и воздействует 1000 раз подряд на рабочую плоскость, то можно утверждать, что на эту плоскость действует импульс в тысячу тонн. Дальше мы будем часто использовать плотность потока энергии и измерять ее будем в киловаттах на квадратный километр или на квадратный метр.
Важнейшим показателем эффективности машины является отношение усилий человека, затрачиваемых на ее обслуживание, к количеству работы, выполняемой этой машиной. Если машина, кроме мускульной силы человека, использует какой-то другой источник энергии (например, энергию животных, воды, ветра или тепла), мы должны подсчитать стоимость этой энергии в единицах общественных затрат на организацию доставки энергии до рабочих мест от этих источников. Эту стоимость мы рассматриваем как капитальные затраты на потребляемую энергию. После этого следует выявить изменения отношения капитальных затрат на одного работника, обслуживающего данный класс машин, к изменению производительности работника, использующего эту машину.
Это отношение можно описать математической функцией. Представим график, в котором ось Y отражает темпы роста выпуска продукции в расчете на одного работника, а ось X отражает повышающуюся стоимость капитальных затрат на потребляемую энергию в расчете на одного работника. Затем добавим ось Z, отражающую рост плотности потока энергии, подаваемой к устройству. В этой части книги обсуждение математических функций такого типа имеет отношение исключительно к только что определенной трехмерной функции.
В процессе передачи энергии для работы машин часть энергии теряется в виде «рассеиваемого тепла» или его эквивалента в других формах. По мере того, как мы значительно повышаем концентрацию мощности, т.е. плотность потока энергии усилий, прилагаемых для выполнения работы, соотношение потерь представляет все больший интерес. Здесь мы сталкиваемся с удивительным и любопытным обстоятельством. Оказывается, что при помощи потока энергии высокой плотности, составляющей лишь часть общей мощности, подаваемой к механизму, можно выполнять больший объем работы, чем при использовании всего потока относительно меньшей ее плотности. Получается, что часть энергии выполняет больший объем работы, чем вся энергия. Это одна из наиболее интересных особенностей экономической науки, которая в большей или меньшей степени свойственна практически всем ее фундаментальным направлениям.
Еще одна важная характеристика столь сильно интересующей нас математической функции – это явление «уменьшения степени отдачи». На каком этапе рост капитальных вложений на одного работника, или повышение плотности потока энергии, уже не позволяет нам достичь тех же темпов отдачи, которые мы наблюдали в предшествующие периоды увеличения интенсивности капитальных затрат, плотности потока энергии или того и другого одновременно?
Эти же принципы применимы, в частности, и в областях сельского хозяйства.
Мы измеряем сельскохозяйственное производство двумя способами: 1) производство продукции на одного работника и 2) урожайность с гектара или квадратного километра. В первом приближении мы измеряем само производство в бушелях зерна, тоннах животноводческой продукции и т.п. В конечном счете, в экономике мы должны определять эту продукцию как компоненты рыночных корзин. Существуют две рыночные корзины:
Используя рыночные корзины как стандарт для учета продукции, мы сравниваем объемы выпуска ее с необходимыми затратами, понесенными обществом для ее производства. Производство должно быть соотнесено с общим количеством квадратных километров, занимаемых данным обществом. Этим учитывается интенсивность его производственной деятельности на квадратный километр, показатель, основанный на принципе плотности потока энергии. Эти два показателя (на квадратный километр и на одного работника) связываются через плотность населения.
На примере сельского хозяйства видно то, как принципы, выявленные при изучении действия тепловых машин, могут быть применены к экономическим процессам в самом широком смысле.
Значение тепловых машин для экономического процесса в целом измеряется экономией общих (и усредненных) человеческих усилий. Суть этой меры раскрывает понятие рыночной корзины, которая имеет одно и то же содержание, но достигнутое меньшими усилиями всего общества, причем это содержание может быть улучшено по количеству и качеству без увеличения усилий, прилагаемых обществом. Другими словами, трудосберегающие технологии – это важнейший результат, рассмотрение которого входит в задачи политической экономии. Это полностью применимо и к счету национального дохода [8].
Мы уже отмечали, что повсеместное использование угля взамен дров, энергии воды и ветра как топлива для машин стало отправной точкой при создании Лейбницем экономической науки. Мы также определили основные характеристики необходимой нам математической функции. Стоимость добычи угля должна сопоставляться с выгодой, получаемой при его сгорании в тепловых машинах. По Лейбницу, назначение тепловых машин – позволить работнику с их помощью выполнить такие объемы работ, которые выполняют «сотни других», не использующих подобных машин. Указанное трудосбережение (экономия труда) должно сравниваться со стоимостью машин и потребляемого ими угля. В стоимость последнего входит его добыча, доставка, а также расходы по его превращению в источник силы, движущей машины.
Несколькими абзацами выше, в нашем первоначальном описании требуемой математической функции, мы ее определили, используя пример сравнения одной машины с другой. Сейчас мы должны обосновать ее заново. Пусть А – это экономия труда, полученная при усовершенствовании производительных сил посредством тепловых машин, а В – это дополнительные затраты общества по производству, ремонту и обеспечению энергией этих машин. Тогда С=А-В, где С – чистый доход общества на душу населения, который должен отражаться на оси Y. Этот доход С становится новым уровнем производства (и потребления) обществом на душу населения, превращаясь в добавок к рыночной корзине. На каком же уровне возрастания капиталоинтенсивности и увеличения плотности потока энергии эта функция дает «снижение отдачи»?
Капиталоинтенсивность принимается приблизительно равной отношению затрат труда (оператора машины) в стоимостном выражении к усредненным затратам труда отдельного работника. Капитальные затраты, использованные для расчета этого отношения, включают труд, необходимый для создания этой машины и поддержки ее в рабочем состоянии, а также для обеспечения ее энергией. Сюда не входят такие статьи «накладных расходов», как администрирование, ненаучные формы обслуживания, затраты по продаже, финансовые выплаты и т.п. .
Что же коррелирует с ростом капиталоинтенсивности? Средняя производительность труда в обществе в целом или же ее рост только в той группе наемных работников, которые заняты в сфере производства? Фактически должны коррелировать обе меры роста средней производительности на душу населения.
Кривая нашей математической функции, отображающей корреляцию роста капиталоинтенсивности со средней производительностью труда, является кривой, описывающей рост способности выполнения работы. Эту функцию мы должны расширить так же, как мы это делали с функцией, описывающей машину несколькими абзацами ранее. Мы должны добавить ось Z – рост плотности потока энергии. Тогда мы получим некую кривую, описывающую «уменьшение отдачи» на каком-то уровне капиталоинтенсивности, при условии, что поток плотности энергии постоянен. В случае постоянства капиталоинтенсивности мы также получим кривую, входящую в область «уменьшения отдачи». Когда обе эти величины растут одновременно, мы получим совершенно иной график. Нас будут интересовать только те кривые, которые содержат как рост капиталоинтенсивности, так и рост плотности потока энергии, но происходящие с разными скоростями. Из них наиболее интересными являются те, для которых относительная степень прироста каждой величины изменяется по линейному или нелинейному закону, т.е. зависимости, в которых степени изменения роста этих величин сами являются математической функцией. Это функция уровня капиталоинтенсивности и плотности потока энергии.
Другими словами, в наиболее интересных случаях невозможно добиться эффективного роста капиталоинтенсивности без одновременной работы в условиях какой-то минимальной плотности потока энергии. Так же невозможно действенно повышать эту плотность без какого-то минимального уровня капиталоинтенсивности. Именно эта ситуация и встречается в реальных экономических процессах.
Представьте ситуацию, при которой две тепловые машины потребляют одно и то же количество энергии в час, но отдельный работник на одной из них получает больший выход продукта, чем на другой. Различие этих двух типов машин состоит в их внутренней организации. Это различие и есть лейбницевское определение технологии (фр. polytechniqие).
Физическая экономика – это исследование обозначенных типов математических функций с позиций технологии.
В первом приближении технология определяется эквивалентным количеством кругового действия для преобразования использованной энергии в работу при помощи машины.
Это напоминает ситуацию в астрономии, когда внутренние процессы машины изучаются в виде циклических изменений в направлении приложенного действия, а общий цикл определяется как совокупность промежуточных циклов. С помощью метода, который Николай Кузанский определил как принцип минимума-максимума, или изопериметрический принцип, задается круговое действие, эквивалентное действию, производимому машиной. Это означает использование принципа наименьшего действия для анализа технологии машинных циклов.
Применение данной методики не связано с тем, что многие машины используют круговое движение. Скорее, это движение является доминирующим, потому что его необходимость определяется физическим принципом природы, соответствующим лейбницевскому принципу наименьшего действия.
Для того, чтобы добавить к нашей общей математической функции ось Z, мы должны отразить рост плотности потока энергии в рамках интерпретации кругового действия. Это приводит к высшей форме кругового действия – коническо-спиральному действию. Глубинная суть этого явления становится ясной после исследования данной характеристики этой функции с точки зрения работ по самоподобным коническо-спиральным функциям, выполненным Гауссом и Риманом.
Следует признать, что за исключением автора и его единомышленников никакие другие организации и институты мира не руководствуются определением Лейбница в экономической науке; автору не известны случаи, когда какой-либо университет трактовал бы экономическую науку как физическую экономику или признавал бы необходимость совместного использования методов физической экономики и математической физики в их взаимодействии при исследовании какого-либо объекта. Новые работы в области физической экономики свелись на нет в результате Венского конгресса 1815 года. Кроме камералистских программ, разработанных Лейбницем или попавших под его влияние, важнейшим центром, который применял принципы физической экономики, была Политехническая школа 1794-1825 годов, руководимая Лазарем Карно и его учителем Гаспаром Монжем. Начиная со ссылки Карно в Германию в 1816 году, его школа попала под влияние Пьера-Симона Лапласа (1749-1827) и начала распадаться. Это продолжалось и во времена Огюстена Коши (1789-1857) [9].
Приложение принципов физической экономики к предмету политической экономии было продолжено, причем плодотворно, после 1815 года такими яркими представителями Американской системы политической экономии, как Фридрих Лист (1789-1846), Генри Ч.Кэри (1793-1879) и Э. Пешайн Смит (1814-1882). Кэри, совместно с Генри Клэем, был лидером Либеральной партии, а также экономическим советником президента Авраама Линкольна. Один из соратников Кэри – Э. Пешайн Смит, будучи с 1872 года советником во время реставрации Мэйдзи в Японии, принимал участие в программах по переходу Японии на индустриальный путь развития. Достижения этой страны до сих пор вызывают чувство зависти во всех концах света. Таким образом, программы этих ученых сохраняли существенное влияние на мировую историю даже после их смерти. Эти программы были не чем иным, как практическим воплощением идей экономической науки, разработанных Лейбницем и его последователями с 1671 по 1815 год. Научное направление Лейбница и его метод в области физической экономики активно поддерживали некоторые крупные институты Германии до самой смерти Гаусса (1855), его ближайшего последователя Лежена Дирихле (1859) и их преемника и соратника – Римана (1866). Хотя Дирихле был протеже Александра фон Гумбольдта, обучался в Политехнической школе, работая совместно с Гумбольдтом, и хотя сам Гумбольдт тайно сотрудничал с Карно до его смерти в 1823 году, тем не менее университетский кружок Гумбольдта в Берлине и его соратники из окружения Гаусса и из Геттингена не распространяли свои открытия в области математической физики на физическую экономику как таковую. Удивительно, что первым, кто осознал основополагающее значение трудов Римана для решения ключевых проблем экономической науки, был автор этой книги. Произошло это в 1952 году.
Среди тех, кто немного разобрался в этой проблеме и осознавал ее значимость, был Генри Ч.Кэри. Примечательной в этом смысле является его работа «Единство закона». Намерения Кэри являются верными, а некоторые его рассуждения, изложенные в этой книге, заслуживают внимания любого серьезного студента-экономиста. Неудачные суждения в его книге вызваны тем, что в тот момент он находился под влиянием авторитета профессора Геттингенского университета Евгения Дюринга [10] – искусственно созданной знаменитости того периода. Находясь под его влиянием, Кэри принимал толкования принципов физики с позиций, противоположных направлению Гаусса и Римана. Таким образом, хотя Кэри верно утверждал, что термодинамика должна быть принята во внимание в экономической науке, он придерживался неверного взгляда на саму термодинамику.
Собственный вклад автора в экономическую науку относится к результатам исследования, впервые проведенного в 1952 году. В результате попыток 1948-1952 годов создать концепцию, опровергающую доктрину «информационной теории» Винера-Шеннона, автор занялся изучением трудов Георга Кантора 1871-1883 годов по трансфинитной упорядоченности. Это привело автора к новому, скорректированному взгляду на римановские работы периода 1852-1859 годов [11]. Он осознал, что римановская математическая физика содержит в себе решение проблемы численной оценки соотношения между темпами технологического прогресса и последующим ростом интенсивности экономического развития. Поэтому метод, разработанный с этих начальных позиций, был назван методом Ларуша – Римана.
Среди слушателей автора книги на лекциях по экономической науке были студенты-математики, специалисты по математической физике и родственным дисциплинам. С помощью их плодотворного взаимодействия в период примерно с 1970 года была осуществлена важная проработка оригинальной формы метода Ларуша-Римана. Эта работа, по профилю относящаяся к экономической науке, пересеклась с двумя такими неразрывно связанными и прогрессирующими темами, как управляемый термоядерный синтез и передовые направления в области физики плазмы. С этой точки зрения традиции Лейбница и Политехнической школы были возрождены.
Ниже мы покажем важность практических проработок в примыкающих областях науки.
Предположим, что в некотором случае мы теряем 80% энергии, поставляемой машине или какому-то процессу. Пусть даже эти потери обусловлены развитием и применением плотности потока энергии, возросшей на несколько порядков. Однако в некоторых из этих случаев мы выполняем большую работу, чем можно было выполнить путем использования всех 100% энергии, но поставляемой на низком уровне плотности ее потока. На этом любопытном явлении мы уже останавливались: простое преобразование энергии в работу является неверным представлением. Этот же феномен не только характеризует процессы в живой материи, но встречается нам и в других областях научных исследований.
Как будет показано ниже, рассмотрение проблем экономической науки с точки зрения метода римановской математической физики приводит нас к своеобразному пониманию понятий «работа» и «энергия», которое отличается от принятого Клаузиусом (1822-1888), Гельмгольцем (1821-1894), Максвеллом (1831-1879) и Больцманом (1844-1906). По мнению Кеплера, а также Гаусса, завершившего работы Кеплера в этом направлении, понятия работы и энергии, извлекаемые из экономической науки, являются верными и соответствуют идеям римановской математической физики как таковой. Ученые-экономисты, таким образом, должны искать в работах физиков и биологов практические примеры, требующие тех же понятий работы и энергии, которые возникают в экономике. Главной целью таких поисков является определение тех физических процессов, которые по своей природе наиболее плодотворны для развития технологии.
Кроме того, что у Римана возникали трудности из-за «инквизиции», проводимой окружением Клаузиуса, Гельмгольца и др. (начиная приблизительно с 1857 г.), все усложняющееся течение болезни лишило его возможности писать уже в начале 60-х годов. И только с началом исследовательских работ над архивами Римана, начатых в 1978 г. и приведших Уве Парпарта-Хенке к изучению архивов Бетти в Италии, нам, наконец, стал по-настоящему известен стиль мышления Римана в период 1860-1866 гг.
Даты 1852-1859 определены следующим образом. Квалификационная диссертация Римана («О гипотезах, на которых покоится геометрия»), опубликованная в 1854 г., но завершенная уже в 1853 году, была одной из трех диссертаций, составленных Риманом под руководством его патрона Гаусса, подготовленная им к аттестации 1853 г. Две другие находятся в архиве неопубликованных работ и являются документами чрезвычайной важности для истории науки, несмотря на весьма ограниченную их известность.
На основании этих свидетельств мы датируем истинно «римановский» период в его математической физике как время написания этих трех нацеленных на будущее квалификационных диссертаций. Год 1859 определяется выпуском труда «О распространении плоских воздушных волн конечной амплитуды», а также моментом, когда большинство римановских работ по электродинамике были завершены. (В 1861 году появились примечания к римановским лекциям по электродинамике в Геттингене, опубликованным Карлом Хаттендорфом в 1875 г.) Кое-кто может отнести начальную дату к более ранней диссертации (1851 г.), а не к подготовке квалификационной; однако споры не стоят затраченных усилий. Таково наше обоснование предложенной датировки этого периода 1852-1859 годами.
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
