содержатся соответственно в
0-ом, 1-ом, 2-ом, 3-ем, 4-ом столбцах матрицы.Поршнев С.В.
Для проверки второго закона Кеплера
необходимо провести сравнение площади,
заметаемой радиус-вектором за равные промежутки
времени, используя значения кинематических
характеристик движения тела в гравитационном
поле, полученные численным решением системы ДУ
(24), (25), возвращенные в матрицу Z. Напомним, что
размерность матрицы Z, содержащей решения
системы ДУ, -- N* 5; нумерация
столбцов и строк матрицы начинается с нулевого
значения; значения t, содержатся соответственно в
0-ом, 1-ом, 2-ом, 3-ем, 4-ом столбцах матрицы.
Так как решение уравнений движения проводится на равномерной временной сетке, то для задания начального и конечного значений временного интервала, в течение которого вычисляется площадь сектора, заметаемого радиус-вектором, достаточно указать номер соответствующей строки матрицы Z и количество используемых точек (т.е. длину временного интервала).
При достаточно малом шаге интегрирования D t уравнений движения
(определяемым количеством точек N, в которых
ищется решение системы ДУ,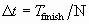 
) площадь, заметаемая радиус вектором
за время D t, примерно равна
площади треугольника с вершинами в точках (0,0),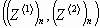 
, 
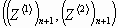(рис. 8).
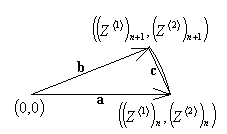
рис. 8
Для вычисления площади треугольника, у которого заданы координаты вершин, можно воспользоваться формулой Герона
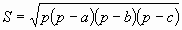, (28)
где p - полупериметр треугольника, изображенного на рис. 8, a, b, c - длины его сторон:
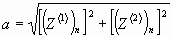, (29)
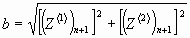, (30)
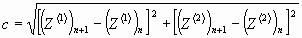. (31)
Однако программа вычисления площади сектора, заметаемого радиус-вектором, получается более компактной, если использовать встроенную в пакет Mathcad функцию, вычисляющую векторное произведение трехмерных векторов. Как известно из аналитической геометрии, площадь треугольника, изображенного на рис. 8, равна
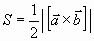, (32)
поэтому алгоритм вычисления площади сектора, заметаемого радиус-вектором, реализуется следующей последовательностью действий:
1. Задание начального момента времени и длины временного интервала.
2. Присвоение координатам вектора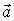 
соответствующих значений координат
орбиты (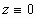
) в момент времени.
3. Присвоение координатам вектора соответствующих значений координат
орбиты (
) в момент времени
.
4. Вычисление площади треугольника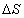 
, заметаемого радиус-вектором на
временном интервале .
5. Нахождение площади, заметаемой радиус-вектором
на временном интервале 
,
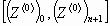суммированием известной площади, заметаемой
радиус-вектором на интервале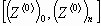 
, и D S.
Для реализации этого алгоритма документ, описанный в предыдущем разделе, необходимо дополнить следующими строками.
1) Задание номера начальной точки, начиная с которой производится вычисление площади, заметаемой радиус-вектором
;
2) Задание количества точек, по которым вычисляется площадь, заметаемая радиус-вектором
;
3) Программа для вычисления площади, реализующая описанный выше алгоритм
Далее, задавая различные начальные значения номера начальной точки, можно убедиться в том, что значение переменной S с определенной точностью остается.
Рис.9
Представляет определенный интерес не только вычислить площадь сектора, заметаемого радиус-вектором, но и изобразить данный сектор на рисунке вместе с траекторией тела. Однако анализ этой задачи обнаруживает известную ограниченность графических возможностей Mathcad, который позволяет изображать на рисунках только функциональные зависимости. Средств, позволяющих нарисовать замкнутую фигуру произвольной формы и залить ее выбранным цветом, разработчики Mathcad, к сожалению, не предусмотрели. Однако выход из данной ситуации все-таки существует. Он состоит в том, чтобы последовательно нарисовать каждый из секторов, заметаемых радиус-вектором за время Dt. Для построения последовательности секторов необходимо сформировать двумерный массив S1, содержащий координаты вершин последовательных треугольников, аппроксимирующих сектор, заметаемый радиус вектором (рис. 9), и затем построить график зависимости, заданной в виде таблицы. Ниже мы приводим текст соответствующей программы, который следует добавить в ранее созданный документ.
Затем построить на одном чертеже орбиту, отметить фокус эллипса, и нарисовать сектор, заметаемый радиус-вектором (рис. 10).
Рис.10
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
