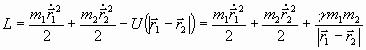MathCAD КМ ТПОИ 3GL к экономической информатике 4GL - визуальным средам

Решение задачи Кеплера в пакете Mathcad

Поршнев С.В.

Уравнения движения планет

В качестве отправной точки решения задачи Кеплера рассмотрим движение двух тел, взаимодействующих друг с другом, считая их при этом материальными точками. Функция Лагранжа такой системы имеет вид

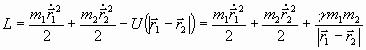, (1)

где 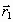, 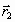- радиус-векторы первого и второго тела, соответственно, 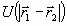- потенциальная взаимодействия тел, g - гравитационная постоянная. Введем вектор, направленный от первого тела ко второму телу

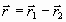. (2)

Тогда в системе отсчета с началом координат в центре масс рассматриваемой системы тел

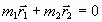. (3)

Из (2), (3) находим:

, (4)

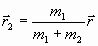. (5)

Подставляя (4), (5) в (1), получаем

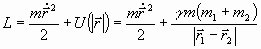, (6)

где введено обозначение

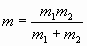. (7)

Величину, определяемую в соответствии с (7), принято называть приведенной массой. Функция (6) формально совпадает с функцией Лагранжа одной материальной точки с массой m, движущейся в потенциале 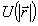, симметричном относительно начала выбранной системы отсчета. Таким образом, задача о движении двух взаимодействующих тел сводится к задаче о движении одного тела с массой m в заданном внешнем поле 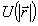, создаваемом неподвижным центром с массой m₁+m₂. Отметим, что если масса одного из взаимодействующих тел значительно меньше массы другого тела, последнее можно рассматривать как неподвижный притягивающий центр, и найденная зависимость 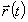будет описывать траекторию движения более легкого тела.

В противном случае, решив задачу о движении тела с массой m в потенциале 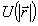по зависимости , в соответствии с (4), (5) находят траектории каждой частицы .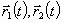

Воспользовавшись уравнениями Лагранжа (здесь обобщенными координатами являются координаты радиус-вектора, обобщенными скоростями - координаты вектора )

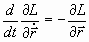, (8)

получим уравнение движения тела

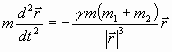, (9)

которое при m₁>> m₂ принимает вид

(10)

в полном соответствии с законом всемирного тяготения Ньютона.

Отметим два важных свойства силы тяготения, вытекающих из (10):

1) сила зависит только от расстояния между телами;

2) сила направлена по прямой, проходящей через центры взаимодействующих тел.

Такие силы называются центральными. Можно показать ([1]), что следствием указанных свойств является сохранение момента импульса тела

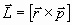, (11)

где .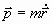

Сохранение момента импульса, в свою очередь, означает, что траектория движения тела в центральном поле лежит в плоскости, которой перпендикулярен вектор 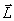. Кроме того, движение тела ограничивается условиями сохранения полной энергии

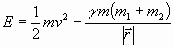(12а)

и величины

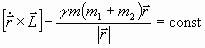. (12б)

Для решения уравнений движения выберем прямоугольную систему координат, начало которой находится в центре масс (рис.1).

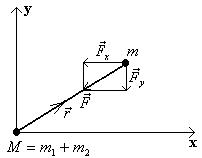
pic0002.jpg (4662 bytes)

Рис.1

(Отметим, что в отличие от аналитического решения, наиболее просто получаемого в цилиндрической системе координат, численное решение задачи Кеплера более удобно проводить в декартовой системе координат). Уравнения движения (9) в выбранной системе координат имеют следующий вид:

, (13)

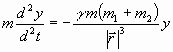. (14)

Введя обозначение и сократив общие множители, запишем выражения (13), (14), составляющие систему ДУ второго порядка, в виде

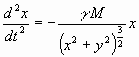, (15)

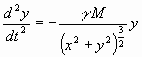. (16)

Предваряя численное решение системы уравнений (15), (16), проведем обезразмеривание этих уравнений. Если в качестве единиц измерения расстояния и времени выбрать радиус орбиты R и период обращения Т, соответствующие движению тела по окружности, то можно ввести безразмерные переменные , , 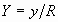. Выполнив в (15), (16) замену переменных x® X, y® Y, t® t , получаем:

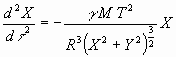, (17)

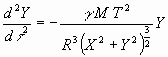. (18)

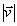Как известно, при движении тела по окружности величина центростремительного ускорения а связана с радиусом круговой орбиты и скоростью тела соотношением

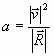. (19)

При движении в гравитационном поле по окружности центростремительное ускорение обусловлено гравитационной силой. Следовательно,

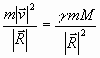, (20)

откуда находим

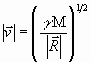. (21)

Выражение (21), являясь общим условием любой круговой орбиты, позволяет найти зависимость периода движения от радиуса орбиты. Период движения

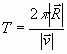, (22)

поэтому, подставив в (22) выражение (21), получим

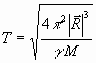. (23)

Подставляя выражение (23) в (17), (18), получаем окончательно обезразмеренную систему уравнений

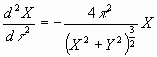, (24)

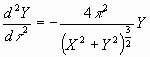. (25)

Из уравнений (24), (25) видна их универсальность - они не зависят ни от периода обращения тела вокруг центра поля, ни от радиуса орбиты. Следовательно, величина 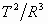, входящая в (17) и (18), одинакова для всех тел, совершающих движение в гравитационном поле по замкнутым траекториям, что является доказательством справедливости третьего закона Кеплера.

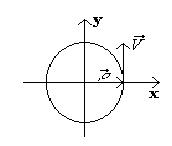
pic0003.jpg (3778 bytes)

Рис.2

При решении системы дифференциальных уравнений будем считать, что в начальный момент времени тело находилось в точке с радиус-вектором 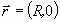, скорость тела была направлена вертикально вверх, (рис. 2). Так как система уравнений (24), (25) является безразмерной, необходимо также привести к безразмерному виду начальные условия. Выполнив, как и выше, замену переменных , , 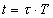приводим начальные условия к следующему виду:

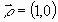, (26)

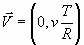, (27)

где T определяется выражением (23).

Однако использовать конкретные числовые значения R, T, M для проверки законов Кеплера не требуется, так как безразмерные начальные условия также обладают известным универсализмом. Для того чтобы это показать, найдем безразмерную скорость тела, движущегося в гравитационном поле по окружности. Подставив (21), (23) в (27), получаем

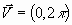. (28)

Следовательно, для получения орбит, отличных от круговых, достаточно задавать значения начальной скорости, отличные от 2p.

на верх MathCAD КМ ТПОИ 3GL к экономической информатике 4GL - визуальным средам

Знаете ли Вы, что в 1974 - 1980 годах профессор Стефан Маринов из г. Грац, Австрия, проделал серию экспериментов, в которых показал, что Земля движется по отношению к некоторой космической системе отсчета со скоростью 360±30 км/с, которая явно имеет какой-то абсолютный статус. Естественно, ему не давали нигде выступать и он вынужден был начать выпуск своего научного журнала "Deutsche Physik", где объяснял открытое им явление. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира