|
|
|
При программировании
сложных изображений, состоящих из множества элементов, используется метод, который
называется методом базовой точки. Суть этого метода заключается в следующем:
1. Выбирается некоторая
точка изображения, которая принимается за базовую.
2. Координаты остальных
точек отсчитываются от базовой точки.
3. Если координаты
точек изображения отсчитывать от базовой в относительных единицах, а не в пикселах,
то обеспечивается возможность масштабирования изображения.
На рис. 10.17 приведено
изображение кораблика. Базовой точкой является точка с координатами (X0
Y0). Координаты остальных точек отсчитываются именно от этой точки.
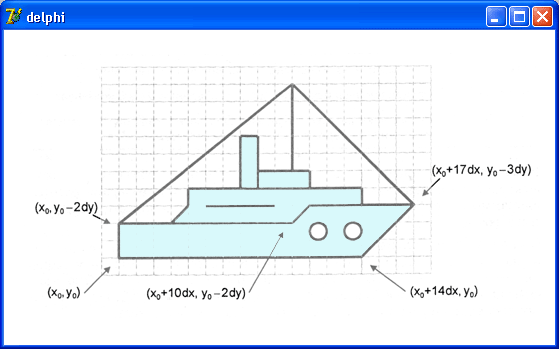
Рис. 10.17. Определение
координат изображения относительно базовой точки
В листинге 10.9 приведен
текст программы, которая выводит на экран изображение перемещающегося кораблика.
Листинг 10.9.
Кораблик
unit
ship_;
interface
uses
Windows, Messages, SysUtils, Classes,
Graphics, Controls, Forms, Dialogs,
StdCtrls,
ExtCtrls;
type
TForm1
= class(TForm)
Timer1:
TTimer;
procedure
Timer1Timer(Sender: TObject);
procedure FormActivate(Sender: TObject);
private
{
Private declarations } public
{
Public declarations } end;
var
Form1:
TForm1;
x,y:
integer; // координаты корабля (базовой точки)
implementation
{$R
*.DFM}
//
вычерчивает кораблик
procedure
Titanik(x,y: integer; // координаты базовой точки
color: TColor); // цвет корабля
const dx = 5; dy = 5;
var
buf: TColor;
begin
with
form1.canvas do begin
buf:=pen.Color; // сохраним текущий цвет
pen.Color:=color;
// установим нужный цвет
//
рисуем . . .
//
корпус MoveTo(x,y);
LineTo(x,y-2*dy) ;
LineTo (x+10*dx, y-2*dy) ;
LineTo (x+ll*dx, y-3*dy) ;
LineTo (x+17*dx,y-3*dy) ;
LineTo (x+14*dx, y) ;
LineTo
(x,y) ;
// надстройка
MoveTo(x+3*dx,y-2*dy) ;
LineTo (x+4*dx, y-3*dy) ;
LineTo (x+4*dx, y-4*dy) ;
LineTo (x+13*dx,y-4*dy) ;
LineTo (x+13*dx, y-3*dy) ;
MoveTo(x+5*dx,y-3*dy) ;
LineTo
(x+9*dx, y-3*dy) ;
//
капитанский мостик
Rectangle
(x+8*dx, y-4*dy, x+ll*dx, y-5*dy)
//
труба
Rectangle
(x+7*dx, y-4*dy, x+8*dx, y-7*dy) ;
//
иллюминаторы
Ellipse
(x+ll*dx,y-2*dy,x+12*dx,y-l*dy) ;
Ellipse
(x+13*dx, y-2*dy, x+14*dx, y-l*dy) ;
//
мачта
MoveTo(.x+10*dx,y-5*dy)
; LineTo(x+10*dx,y-10*dy);
//
оснастка
MoveTo(x+17*dx,y-3*dy);
LineTo(x+10*dx,y-10*dy);
LineTo(x,y-2*dy);
pen.Color:=buf; // восстановим старый цвет карандаша
end;
end;
//
обработка сигнала таймера
procedure TForm1.Timer1Timer(Sender: TObject);
begin
Titanik(x,y,form1.color); // стереть рисунок
if x < Form1.ClientWidth
then x := x+5
else begin // новый рейс x := 0;
у := Random(50) + 100;
end;
Titanik(x,у,clWhite);
// нарисовать в новой точке end;
procedure TForml.FormActivate(Sender: TObject);
begin
x:=0;
y:=100;
Form1.Color:=clNavy;
Timerl.Interval := 50; // сигнал таймера каждые 50 миллисекунд
end;
end.
Отрисовку и стирание изображения кораблика выполняет процедура Titanik, которая получает в качестве параметров координаты базовой точки и цвет, которым надо вычертить изображение кораблика. Если при вызове процедуры цвет отличается от цвета фона формы, то процедура рисует кораблик, а если совпадает — то "стирает". В процедуре Titanik объявлены константы dx и dy, определяющие шаг (в пикселах), используемый при вычислении координат точек изображения. Меняя значения этих констант, можно проводить масштабирование изображения.
|
|
|
Дело в том, что в его постановке и выводах произведена подмена, аналогичная подмене в школьной шуточной задачке на сообразительность, в которой спрашивается:
- Cколько яблок на березе, если на одной ветке их 5, на другой ветке - 10 и так далее
При этом внимание учеников намеренно отвлекается от того основополагающего факта, что на березе яблоки не растут, в принципе.
В эксперименте Майкельсона ставится вопрос о движении эфира относительно покоящегося в лабораторной системе интерферометра. Однако, если мы ищем эфир, как базовую материю, из которой состоит всё вещество интерферометра, лаборатории, да и Земли в целом, то, естественно, эфир тоже будет неподвижен, так как земное вещество есть всего навсего определенным образом структурированный эфир, и никак не может двигаться относительно самого себя.
Удивительно, что этот цирковой трюк овладел на 120 лет умами физиков на полном серьезе, хотя его прототипы есть в сказках-небылицах всех народов всех времен, включая барона Мюнхаузена, вытащившего себя за волосы из болота, и призванных показать детям возможные жульничества и тем защитить их во взрослой жизни. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
