|
|
|
Поверхности, на которую
программа может осуществлять вывод графики, соответствует объект Canvas. Свойство
pixels, представляющее собой двумерный массив типа TColor, содержит информацию
о цвете каждой точки графической поверхности. Используя свойство Pixels, можно
задать тре-
буемый цвет для любой
точки графической поверхности, т. е. "нарисовать" точку. Например,
инструкция
Form1.Canvas.Pixels[10,10]:=clRed
окрашивает точку поверхности
формы в красный цвет.
Размерность массива
pixels определяется размером графической поверхности. Размер графической поверхности
формы (рабочей области, которую также называют клиентской) задается значениями
свойств ciientwidth и ClientHeight, а размер графической поверхности компонента
image — значениями свойств width и Height. Левой верхней точке рабочей области
формы соответствует элемент pixels [0,0], а правой нижней -Pixels[Ciientwidth
- 1,ClientHeight - 1].
Свойство Pixels можно
использовать для построения графиков. График строится, как правило, на основе
вычислений по формуле. Границы диапазона изменения аргумента функции являются
исходными данными. Диапазон изменения значения функции может быть вычислен.
На основании этих данных можно вычислить масштаб, позволяющий построить график
таким образом, чтобы он занимал всю область формы, предназначенную для вывода
графика.
Например, если некоторая
функция f(x) может принимать значения от нуля до 1000, и для вывода ее графика
используется область формы высотой в 250 пикселов, то масштаб оси Y вычисляется
по формуле: т = 250/1000. Таким образом, значению f(x) = 70 будет соответствовать
точка с координатой Y =233. Значение координаты Y вычислено по формуле
Y= h -f(x) х т = 250 - 70х(250/1000),
где h - высота области
построения графика.
Обратите внимание на
то, что точное значение выражения 250 - 70х(250/1000) равно 232,5. Но т. к.
индексом свойства pixels, которое используется для вывода точки на поверхность
Canvas, может быть только целое значение, то число 232,5 округляется к ближайшему
целому, которым является число 233.
Следующая программа,
текст которой приведен в листинге 10.5, используя свойство pixels, выводит график
функции у = 2 sin(jc) e*/5. Для построения графика используется вся
доступная область формы, причем если во время работы программы пользователь
изменит размер окна, то график будет выведен заново с учетом реальных размеров
окна.
Листинг 10.5.
График функции
unit
grfunc_;
interface
Windows, Messages, SysUtils, Classes,
Graphics,
Controls, Forms, Dialogs;
type
TForm1
= class(TForm)
procedure FormPaint(Sender: TObject);
procedure FormResize(Sender: TObject);
private
{ Private declarations }
public
{Public declarations }
end;
var
Forml:
TForml;
implementation
{$R
*.DFM}
// Функция, график которой надо построить
Function f(x:real):real;
begin
f:=2*Sin(x)*exp(x/5) ;
end;
//
строит график функции
procedure
GrOfFunc;
var
x1,x2:real; // границы изменения аргумента функции
y1,y2:real; // границы изменения значения функции
х:real; // аргумент функции
у:real; // значение функции в точке х
dx:real;
// приращение аргумента
l,b:integer; // левый нижний угол области вывода графика
w,h:integer; // ширина и высота области вывода графика
mx,my:real; // масштаб по осям X и Y
х0,у0:integer;
// точка — начало координат
begin
//
область вывода графика
l:=10;
// X — координата левого верхнего угла
b:=Forml.ClientHeight-20;
//У
— координата левого верхнего угла
h:=Forml.ClientHeight-40;
// высота
w:=Forml.Width-40;
// ширина
x1:=0;
// нижняя граница диапазона аргумента
х2:=25; // верхняя граница диапазона аргумента
dx:=0.01;
// шаг аргумента
//
найдем максимальное и минимальное значения
//
функции на отрезке [x1,x2]
y1:=f(xl);
// минимум
y2:=f(xl);
//максимум
x:=x1;
repeat
У
:= f (х);
if
у < yl then yl:=y;
if
у > у2 then y2:=y;
х:=x+dx;
until (x >= х2);
//
вычислим масштаб
my:=h/abs(y2-yl);
// масштаб по оси Y
mx:=w/abs(x2-xl);
// масштаб по оси X
х0:=1;
у0:=b-Abs(Round(y1*my))
;
with
form1.Canvas do
begin
//
оси
MoveTo(l,b);LineTo(l,b-h);
MoveTo(x0,y0);LineTo(x0+w,y0);
TextOut(l+5,b-h,FloatToStrF(y2,ffGeneral,6,3));
TextOut(l+5,b,FloatToStrF(yl,ffGeneral,6,3));
//
построение графика
x:=xl;
repeat
y:=f(x);
Pixels[x0+Round(x*mx),y0-Round(y*my)]:=clRed;
x:=x+dx;
until (x >= x2);
end;
end;
procedure TForm1.FormPaint(Sender: TObject);
begin
GrOfFunc;
end;
// изменился размер окна программы
procedure TForm1.FormResize(Sender: TObject);
begin
//
очистить форму
forml.Canvas.FillRect(Rect(0,0,ClientWidth,
ClientHeight));
//
построить график
GrOfFunc;
end;
end.
Основную работу выполняет
процедура GrOfFunc, которая сначала вычисляет максимальное (у2) и минимальное
(yl) значения функции на отрезке [x1l,x2]. Затем, используя информацию о ширине
(Forml.Clientwidth -40) и высоте (Form1.ClientHeight - 40) области вывода графика,
вычисляет масштаб по осям X (mх) иY(mу).
Высота и ширина области
вывода графика определяется размерами рабочей (клиентской) области формы, т.
е. без учета области заголовка и границ. После вычисления масштаба процедура
вычисляет координату у горизонтальной оси (уо) и вычерчивает координатные оси
графика. Затем выполняется непосредственное построение графика (рис. 10.10).
Вызов процедуры GrOfFunc
выполняют процедуры обработки событий onPaint и onFormResize. Процедура TForm1.
FormPaint обеспечивает вычерчивание графика после появления формы на экране
в результате запуска программы, а также после появления формы во время работы
программы, например, в результате удаления или перемещения других окон, полностью
или частично перекрывающих окно программы. Процедура TForm1.FormResize обеспечивает
вычерчивание графика после изменения размера формы.
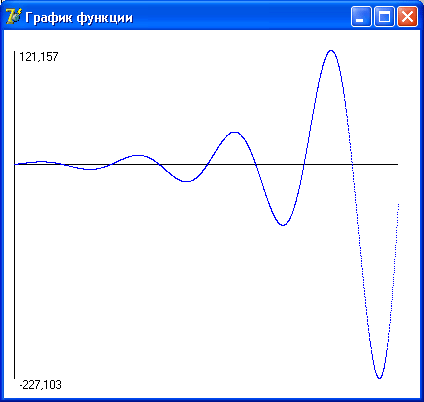
Рис. 10.10. График,
построенный процедурой GrOfFunc
Приведенная программа
довольно универсальна. Заменив инструкции в теле функции f (х), можно получить
график другой функции. Причем независимо от вида функции ее график будет занимать
всю область, предназначенную для вывода.
Примечание
Рассмотренная программа работает корректно, если функция, график которой надо построить, принимает как положительные, так и отрицательные значения. Если функция во всем диапазоне только положительная или только отрицательная, то в программу следует внести изменения. Какие — пусть это будет упражнением для читателя.
|
|
|
Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.
Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.
Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.
Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.
|
|
 |
