A. L. Dmitriev
Baltic State Technical University «VOENMEH»,
1 Krasnoarmeyskaja str. 190005, St. Petersburg, Russia
Abstract. Temperature dependence of the force of gravity is one of the important problems in physics. Body’s absolute temperature characterizes body’s internal energy, related to chaotic movement of its particles. Additionally, temperature defines speed and acceleration of body’s mircoparticles. Theory of Relativity hypothesizes that the “weight of energy” positively affects weight of the body based on temperature increase. Such dependence has not yet been proven by laboratory experiments due to extremely low value of expected effect. Instead, kinematic nature of the dependence of the force of gravity from temperature related to accelerated movement of body’s microparticles, explains relatively strong negative temperature dependence of the weight which have been observed during experiments. Such effects suggest need for deeper research of gravity and will have important scientific and practical value.
Keywords: gravitation, temperature, weight, acceleration, space experiment
Introduction
The problem of the absolute body temperature influence on the strength of the gravitational interaction has long ago started to attract the attention. According to the theory of relativity, the physical weight (excluding the influence of artifacts) of heated body is greater than of a cold one. The amount of extra "energy weight" is extremely small and almost unavailable for direct measurements. The report provides an overview of experiments based on accurate laboratory weighing of heated bodies, in which a negative temperature dependence of the physical weight of bodies is observed. A space experiment is suggested to testify the temperature dependence of the weight, based on the measurement of the radial position of the heated sample located on the orbit of the Earth's satellite.
Laboratory experiments confirming negative temperature dependence of bodyweight
Temperature
dependence of the weight is characterized by the following parameter
![]() ,
where
,
where
![]() is a change of bodyweight and
is a change of bodyweight and
![]() is a change of its absolute temperature. Theory of Relativity states
that temperature change of gravitational body mass
is a change of its absolute temperature. Theory of Relativity states
that temperature change of gravitational body mass
![]() is
related to the change
is
related to the change
![]() of its thermal energy,
of its thermal energy,
![]() ,
where
,
where
![]() (
(![]() -
is specific heat of material,
-
is specific heat of material,
![]() - is speed of light), coefficient
- is speed of light), coefficient
![]() is positive; i.e. its value for the sample of iron
is positive; i.e. its value for the sample of iron
![]() is approximately
is approximately
![]() .
Heating of such sample weighing
.
Heating of such sample weighing
![]() to
to
![]() causes
relative increase in its weight by
causes
relative increase in its weight by
![]() ,
which is impossible to measure during experiments in the lab.
,
which is impossible to measure during experiments in the lab.
In
the meantime, laboratory measurements of the weight of heated bodies
described below demonstrate that coefficient
![]() is negative and its value is much higher than the value provided
above.
is negative and its value is much higher than the value provided
above.
1.1. Measuring the force of gravity dependence from temperature on a torsion balance
Show
and Davy used torsion balance [1] to measure effect of temperature on
the force of gravity. Even though authors concluded that temperature
change of the force of gravity have not been noticed, more careful
analysis of results [2] showed that during these experiments negative
temperature dependence of the force of gravity was present.
Temperature coefficient was
![]() .
.
Data shift to the right of relatively zero point of abscissa on provided histogram corresponds to a decrease of the weight of heated sample.

Figure 1. Generalized results obtained by Show and Davy [2]. Sequence number of measurements is shown on an ordinate, horizontal scale illustrates position of torsion balance rocker.
Weighing of heated samples on high precision analytical balance
In their popular book “Evolution of Physics”, Einstein and Infeld argued that according to the Theory of Relativity heated piece of metal weighs more than a cold one. In the 90s, publications [3-6] state that experimental data pointing towards negative temperature dependence of the weight of non-magnetic metal s

amples have been achieved. Image of samples in Duare’s container heated by ultrasound is presented on Figure 2.
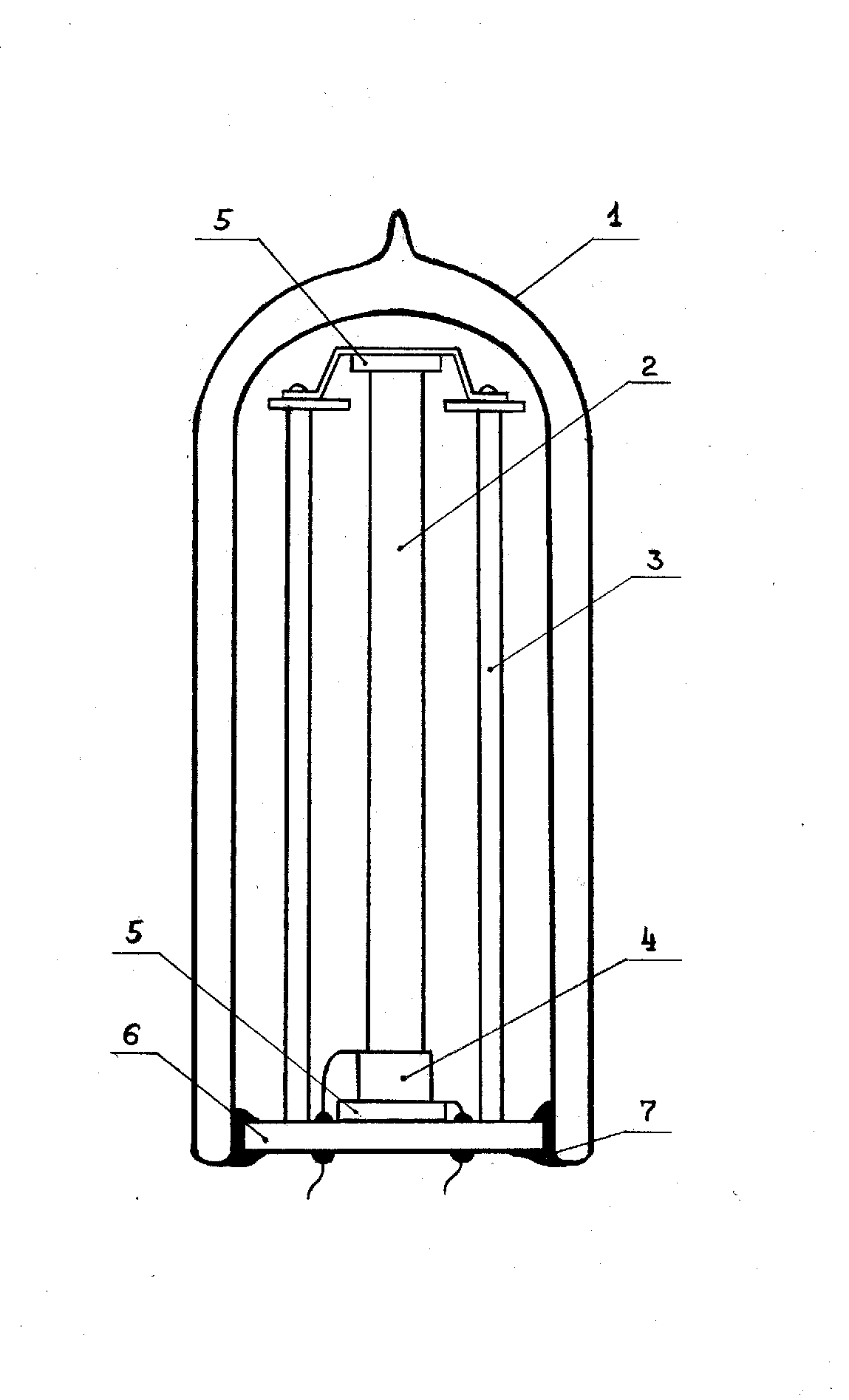
Layout
of Hermetically Sealed Container. 1 – Dewar Flask; 2 – Metal Rod; 3 – Holder Support;
4 – Electroacoustic Transducer (PZT); 5 – Gaskets (Foam Plastic); 6 – Holder Base (Ebonite); 7 – Cold
Welding.
Figure 2. Image of weighed metal samples
Experimental time dependence of the weight of heated sample presented on Figure 3.
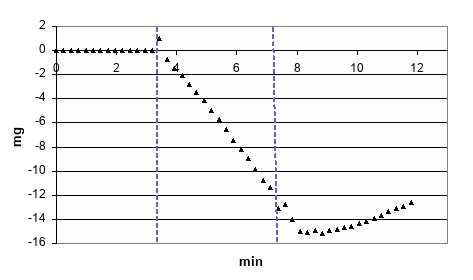
Figure 3. Example of experimental time dependence of the weight of heated sample. Dashed lines show moments when heater was turned on and off.
Experimental
values of temperature coefficient
![]() of
different types of non-magnetic materials are listed in Table
1;
where
of
different types of non-magnetic materials are listed in Table
1;
where
![]() is density,
is density,
![]() is speed of sound.
is speed of sound.
Table 1.
|
Sample |
Lead |
Copper |
Brass |
Titanium |
Duralumin |
PZT |
|
|
11.34 |
8.89 |
8.55 |
4.50 |
2.79 |
7.20 |
|
|
2.64 |
3.80 |
3.45 |
5.07 |
5.20 |
3.50 |
|
|
4.5 |
6.5 |
4.5 |
8.7 |
11.6 |
2.8 |
There
is an increase of
![]() value along with decrease of
value along with decrease of
![]() value of the material.
value of the material.
Negative temperature dependence of the weight of non-magnetic metal samples is being observed during their electric (Figure 4) or chemical heating.
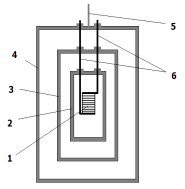
Figure 4. The design of container with electrical heater. 1 - a copper sample with a
winding of an electric heater; 2,3 - cylinders from titan; 4 - cylinder
from brass; 5 - a wire of suspension bracket of container; 6 – copper conductors
Example of temperature change of the weight of container with the metal sample in it connected to electric heater is shown on Figure 5 [7].
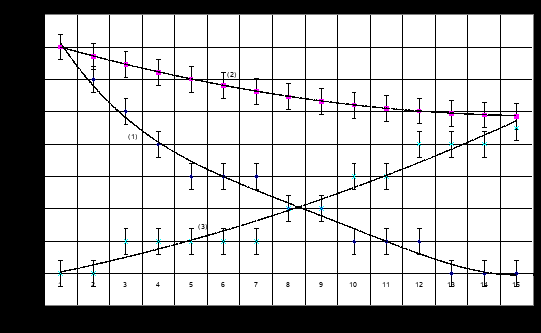
Figure 5. 1 - experimental temporary dependence of the weight of container; 2- calculated dependence of weight taking into consideration effect of temperature convection of the air; 3- change of temperature of the surface of external cylinder.
1. 3. Chemical heating of the sample body [7,8].
The design of container, in which heating of a tight steel cylinder made of stainless steel was carried out by a chemical method, is shown in Figure 6.
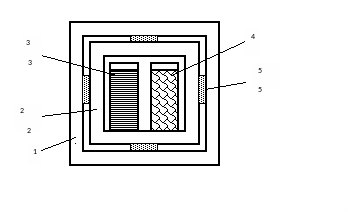
Figure 6. The design of container with chemical heating of the internal cylinder (before overturn). 1 - the external cylinder; 2 - the internal cylinder; 3 - an open vessel with distilled water; 4 - an open vessel with crystals of NaOH; 5 - polyfoam
Diameter of the external brass-cylinder is 60 mm, height - 62 mm, thickness of walls - 3.5 mm, weight - 475 g; diameter of the internal cylinder - 45 mm, height - 46 mm, thickness of walls - 4.5 mm, weight - 280 g. In the condition specified in the figure the temperature of the internal cylinder is constant, the weight of completely equipped container is equal to 773.7651g.
Measurements of weight with a margin error readout of 0.1 mg were also carried out with laboratory scale of XP2004S mark at temperature of air in a working room equal to 19.8 0C, humidity - 31.8 %, pressure - 1022 hPa.
In the course of measurements the container was overturned, then the current value of its weight was registered. In the overturned condition, inside the small cylinder, there is going a process of partial dissolution of crystals NaOH (masse of 5 mg) in distilled water (masse of 6 mg) which is accompanied by heat release. The temperature of the mix in the first seconds of reaction grows by 10 0C, and, as have been shown by special measurements, the average temperature of the internal temperature of the mix in the first seconds of reaction grows by 10 0C, and, as have been shown by special measurements, the average temperature of the internal cylinder, owing to a heat transfer, is smoothly increased by 3-4 0C within the first two-three minutes. A specific feature of the given experiment is that, first, the process of dissolution of crystals of alkali is not accompanied by release of gases and, due to reliable sealing of covers of containers, the release of air from small and big cylinders (and the corresponding handicap to weighing) is absent. Second, due to the big weight of the external cylinder, the temperature of its surface, owing to a heat transfer, increases during the first two minutes by no more than by 0.2 0C. As a result, apparent reduction of weight of the container caused by air convection, which is determined by differences of temperatures of the surface of the container and the ambient air, in the first 2-3 minutes of measurements does not exceed 0.1 mg. High durability of the external cylinder also practically excludes influence of its weak temperature deformations on change of buoyancy of the weighed container.

Figure 7. 1 - experimental time dependence of change of weight of container in the overturned position; 2 - calculated dependence of change of weight of the container with account for influence of temperature air convection; 3 - experimental dependence of temperature of the surface of the external cylinder
Figure 7. shows experimental time dependences of weight of container, temperatures of its surface, and the calculated value of weight caused by temperature convection of air close to the walls of the container. Obviously, the paths of curves 1 and 2 essentially differ, accompanied by a typical sharp fall of weight of the container during the first minutes of measurements.
Let's
estimate influence of temperature artefacts on the results of
measurements of weights of samples. Change
![]() of
apparent weight of the container, caused by change of volume of the
steel cylinder owing to thermal expansion of its material is equal to
of
apparent weight of the container, caused by change of volume of the
steel cylinder owing to thermal expansion of its material is equal to
![]() ,
(1)
,
(1)
where
![]() - density of air,
- density of air,
![]() - factor of linear expansion of material of the cylinder,
- factor of linear expansion of material of the cylinder,
![]() -
its diameter,
-
its diameter,
![]() -
height. Change
-
height. Change
![]() of
apparent weight of the container, caused by deformations of walls of
the cylindrical vessel, owing to temperature change
of air pressure
of
apparent weight of the container, caused by deformations of walls of
the cylindrical vessel, owing to temperature change
of air pressure
![]() within its volume, as it is possible to show on the basis of the
theory of elasticity [8], is equal to:
within its volume, as it is possible to show on the basis of the
theory of elasticity [8], is equal to:
![]() (2)
(2)
where
![]() -
thickness of walls,
-
thickness of walls,
![]() -
the modulus of elasticity and
-
the modulus of elasticity and
![]() -
Poisson’s ratio . The size
-
Poisson’s ratio . The size
![]()
![]() is
connected to change of temperature
is
connected to change of temperature
![]() of
air within the volume of the external cylinder
of
air within the volume of the external cylinder
![]() ,
where
,
where
![]() -
normal pressure of atmosphere and
-
normal pressure of atmosphere and
![]() -
temperature of air in the cylinder. The given estimate is
overestimated, as in the second addend of formula 2, describing
deformation of face walls of a vessel, such walls are presented by
thin membranes; actually, the deflection of end faces is less than it
is supposed in conclusion 2.
-
temperature of air in the cylinder. The given estimate is
overestimated, as in the second addend of formula 2, describing
deformation of face walls of a vessel, such walls are presented by
thin membranes; actually, the deflection of end faces is less than it
is supposed in conclusion 2.
The
change
![]() of
apparent weight of the container, caused by
air
convection due to difference
of
apparent weight of the container, caused by
air
convection due to difference
![]() of
temperatures of surface of the external steel cylinder and
temperatures of air in the closed box of analytical balance, will be
estimated on the basis of [10] according to which
of
temperatures of surface of the external steel cylinder and
temperatures of air in the closed box of analytical balance, will be
estimated on the basis of [10] according to which
![]() (3)
(3)
where
the area of lateral surface of the cylinder is
![]() .
.
In
Table
2
the experimental and calculated values of change of weight of
container, corresponding to the third minute of measurements are
given. In the given calculations the density of air
![]() ,
,
![]() (obviously
overestimated value),
(obviously
overestimated value),
![]() .
.
Table 2.
Calculated
Total
(![]() )
and
experimental
(
)
and
experimental
(![]() )
)
|
|
|
|
|
|
|
|
mcg |
mcg |
mcg |
mcg |
mcg |
|
60 |
62 |
3.5 |
18.9 |
0.36 |
9 |
0.22 |
2.6 |
|
54 |
|
640 |
Obviously, observable (registered) reduction of weights of containers essentially, with account for errors of measurements, exceeds calculated one.
1.4. Experiments of A. P. Shegolev, Fan Liangzao et.al.
In
the 90s, Leningrad engineer A.P. Shegolev measured the weight of
steel ball heated by radiation of powerful laser being inserted into
conical opening in the side of the ball. During heating of the ball
weighing 4.2 kg by 300 degrees, its weight decreased by 3 g, which is
equal to coefficient of
![]() .
.
Chinese
scientists Fan Liangzao, Feng Jinsong and Liu Wu Qing in their
experiments demonstrated that with the change of temperature of
weighed metal sample from 1000 °Ñ
to 6000 °C relative decrease in their weight was 0,5% to 0,8%, which
is equal to
![]() [5].
[5].
Temperature decrease of the weight of metal surfaces deposited in vacuum was outlined in the publication of M. N. Rocklein and S. M. George [6].
1.5. Decrease of the weight of optical fiber during radiation of semiconductor laser also confirms negative temperature dependence of the force of gravity [11,12].
Fluctuation of measurements of balance is being compensated by decrease of temperature of the weight of fiber optics. Vertical lines indicate moments when laser was turned on and off.
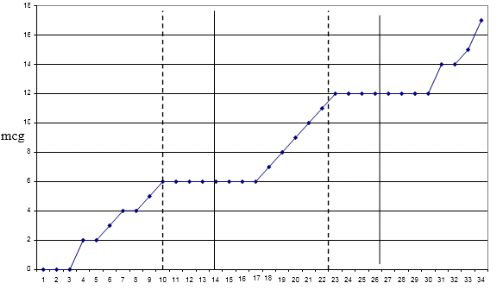
Figure 8. Temporary change of the weight of container [12]. Horizontal scale - number of measurement
2. Thermogravimety [8]
At
creation of a basic curve the seeming mass
![]() of the holder (crucible) in air is equal
of the holder (crucible) in air is equal
![]() ,
where
,
where
![]() -
the mass of a crucible,
-
the mass of a crucible,
![]() -
its volume and
-
its volume and
![]() - air density. Temperature change of the seeming weight
- air density. Temperature change of the seeming weight
![]() ,
(4)
,
(4)
where
![]() ,
,
![]() - volume expansion coefficient of material of a crucible.
- volume expansion coefficient of material of a crucible.
Let’s
![]() ;
;
![]() ;
;
![]() .
.
For
numerical estimates we will use results of [9]. Volume coefficient of
expansion
![]() and, for example, at
and, for example, at
![]() ,
the values of coefficients
,
the values of coefficients
![]() are equal
are equal
![]() and
and
![]() .
As the absolute values
.
As the absolute values
![]() ,
the main contribution to the seeming change of mass of a crucible is
made by the effects of buoyancy described by coefficient
,
the main contribution to the seeming change of mass of a crucible is
made by the effects of buoyancy described by coefficient
![]() .
Obviously, the consent of the experimental and provided settlement
data is possible only at
.
Obviously, the consent of the experimental and provided settlement
data is possible only at
![]() This
fact directly confirms the negative temperature dependence of weight
of bodies.
Temperature change of weight of the holder, it is generally connected
with change of temperature of a porcelain crucible, the assessment of
size of relative temperature change of the weight of porcelain from
where follows the
This
fact directly confirms the negative temperature dependence of weight
of bodies.
Temperature change of weight of the holder, it is generally connected
with change of temperature of a porcelain crucible, the assessment of
size of relative temperature change of the weight of porcelain from
where follows the
![]() Sign and an order of the specified size correspond to data of
measurements of physical temperature dependence of weight of metals
[3-6], and PZT-ceramic [10].
Sign and an order of the specified size correspond to data of
measurements of physical temperature dependence of weight of metals
[3-6], and PZT-ceramic [10].
3. Form of the channel of glow discharge
Arched form of glow discharge which temperature reaches several thousand degrees, under pressure of 0.1 atmosphere and amperage of 30-70mA (Figure 9), is a consequence of temperature dependence of gravity affecting the discharge plasma. In [13,14] it is shown that form of such glow discharge is affected by gravity field pushing plasma, which demonstrates the effect of temperature on the force of gravitation.

Figure 9. Arched form of glow discharge
Simple Phenomenological Model of negative temperature dependence of the gravity force [3,7,10]
Proceeding
from the principle of inertness of mechanical system, that is, its
tendency to preserve the stable state, accelerated under action of
external, for example, elastic force of movement of a test body
downwards should cause an increment
![]() of acceleration of the gravity applied to a body which is directed
from the centre of the Earth. On the contrary, the accelerated
movement of a trial body upwards is accompanied by increase of
acceleration of the gravity applied to a body by value
of acceleration of the gravity applied to a body which is directed
from the centre of the Earth. On the contrary, the accelerated
movement of a trial body upwards is accompanied by increase of
acceleration of the gravity applied to a body by value
![]() .
Values
.
Values
![]() and
and
![]() ,
generally speaking, can be different. Change of acceleration of the
gravity acting on a body, moving with acceleration
,
generally speaking, can be different. Change of acceleration of the
gravity acting on a body, moving with acceleration
![]() under influence of the elastic force, in the elementary (linear)
approximation, is represented as
under influence of the elastic force, in the elementary (linear)
approximation, is represented as
![]() ,
(5)
,
(5)
where
symbols
![]() mean passing
mean passing
![]() and a contrary
and a contrary
![]() ,
in relation to a direction of vector
,
in relation to a direction of vector
![]() of normal acceleration of a gravity, orientation of a vertical
projection of vector
of normal acceleration of a gravity, orientation of a vertical
projection of vector
![]() of acceleration of external forces, and factors
of acceleration of external forces, and factors
![]() and
and
![]() characterize a degree of change of values
characterize a degree of change of values
![]() .
.
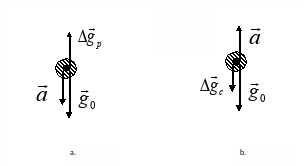
Figure
10.
(a)
Changes in gravity force acceleration acting on test body while body is falling down with acceleration;
(b) Changes in gravity force acceleration while body is moving up with acceleration.
If
the body under action of the external, electromagnetic in nature,
elastic force makes harmonious oscillations along a vertical with
frequency
![]() and amplitude
and amplitude
![]() ,
the average for the period
,
the average for the period
![]() of fluctuations value
of fluctuations value
![]() of change of acceleration of free falling (AFF) of such mechanical
oscillator is equal to the sum of average changes of AFF in movement
of a body passing and contrary to vector
of change of acceleration of free falling (AFF) of such mechanical
oscillator is equal to the sum of average changes of AFF in movement
of a body passing and contrary to vector
![]() ,
,
![]() ,
(6)
,
(6)
and
at constant
![]() it is equal
it is equal
![]() .
(7)
.
(7)
From
3, it follows that at
![]() ,
the average acceleration of free falling of mechanical oscillator,
for example, a rotor with a horizontal axis of rotation, is less than
value
,
the average acceleration of free falling of mechanical oscillator,
for example, a rotor with a horizontal axis of rotation, is less than
value
![]() of normal acceleration of the gravity force. The reduction, averaged
on several series of the measurements of the apparent weight of a
rotor with horizontal axis, was observed in experiment [7], by
results of which for the material of a rotor (stainless steel) it is
possible to approximately estimate the order of value of difference
of normal acceleration of the gravity force. The reduction, averaged
on several series of the measurements of the apparent weight of a
rotor with horizontal axis, was observed in experiment [7], by
results of which for the material of a rotor (stainless steel) it is
possible to approximately estimate the order of value of difference
![]() .
.
If
to consider as the mentioned above trial body a microparticle of a
solid body bound together by forces of interatomic interaction with
other similar particles, formulas 1-3 allow to explain influence of
temperature on acceleration of free falling (weight) of such body.
Thermal movement of microparticles of a solid body is accompanied by
their significant accelerations, in so doing, the average value
![]() of a projection of these accelerations on a vertical is proportional
to average speed of chaotic movement of microparticles. In a
classical approximation, at a body temperature higher than the one of
Debye-temperatures, the acceleration
of a projection of these accelerations on a vertical is proportional
to average speed of chaotic movement of microparticles. In a
classical approximation, at a body temperature higher than the one of
Debye-temperatures, the acceleration
![]() is in direct ratio to a square root from an absolute body
temperature
is in direct ratio to a square root from an absolute body
temperature
![]() ,
where
,
where
![]() - the factor dependent on physical properties of a material.
- the factor dependent on physical properties of a material.
In one-dimensional approximation, we can consider a test body as a chain of microparticles bound by elastic forces
![]() ,
(8)
,
(8)
where
![]() - speed of a longitudinal acoustic wave in a solid test body and
- speed of a longitudinal acoustic wave in a solid test body and
![]() -
its density.
-
its density.
Formally,
having replaced in equation (6) the average for the period of
fluctuations magnitude of acceleration
![]() with average acceleration of particles
with average acceleration of particles
![]() ,
we shall present the temperature dependence
,
we shall present the temperature dependence
![]() of weight of a body as
of weight of a body as
![]() ,
(9)
,
(9)
where
![]() -
weight of a body,
-
weight of a body,
![]() . Negative
temperature dependence of weight of not-magnetic metal samples at
close to normal (
. Negative
temperature dependence of weight of not-magnetic metal samples at
close to normal (![]() )
temperatures of bodies experimentally proves to be true, in so doing,
the relative change of weight for a unit of temperature
)
temperatures of bodies experimentally proves to be true, in so doing,
the relative change of weight for a unit of temperature
![]() ,
(10)
,
(10)
is
equal to several units
![]() [3,4].
[3,4].
The
typical increase of value
![]() along with reduction of density of a sample material is observed that
is in agreement with (4), Table
1
(we should note that outside the limits of considered classical
approximation, for example, at close to zero absolute temperatures of
bodies, formulas 5,6 are not satisfied).
along with reduction of density of a sample material is observed that
is in agreement with (4), Table
1
(we should note that outside the limits of considered classical
approximation, for example, at close to zero absolute temperatures of
bodies, formulas 5,6 are not satisfied).
Weight of oscillator in a variable field of gravitation
Ballistic gravimeters with the test body executed in the form of a mechanical rotor with a horizontal axis of rotation should also be considered as new and perspective means of high-frequency (HF) gravimetry [11]. Rotary motion corresponds to two oscillatory motions of the rotor particles along the orthogonal axis of coordinates. The accelerated harmonic motion of the rotor particles on a vertical is characterized by an infinite set of time derivates. In these condition the interaction of such rotor with a non-stationary gravitational field of the Earth can have a specific, not trivial character. Such researches will promote obtaining the new data on dynamic characteristics and specific features of the gravitational field of the Earth.
We
will
note
that square dependence
![]() shows
that changes of weight of the oscillator will be considerable owing
to thermal fluctuations of particles of material of the oscillator
which frequency is in hyper-sound area.
shows
that changes of weight of the oscillator will be considerable owing
to thermal fluctuations of particles of material of the oscillator
which frequency is in hyper-sound area.
Some interesting and deserving attention results turn out at calculations of change of weight of the mechanical oscillator which is freely falling in a variation field of gravitation.
We
shall present elementary time dependence
![]() as
as
![]() , (11)
, (11)
where
![]() – frequency of changes of FFA value,
– frequency of changes of FFA value,
![]() -
their relative amplitude,
-
their relative amplitude,
![]() -
the phase. Acceleration
-
the phase. Acceleration
![]() of
the material point making harmonious oscillations along a vertical
with amplitude
of
the material point making harmonious oscillations along a vertical
with amplitude
![]() is equal to
is equal to
![]() (12)
(12)
where
![]() - frequency of oscillations.
- frequency of oscillations.
The
averages for oscillation half-cycle
![]() of
values of changes of accelerations
of
values of changes of accelerations
![]() and
and
![]() are equal to
are equal to
![]() (13)
(13)
![]() (14)
(14)
The relative change of FFA of the oscillator, in view of 3, shall be presented as
![]() (15)
(15)
where
![]() ,
,
![]() and frequency function
and frequency function
![]() is equal t
is equal t
 (16)
(16)
here
![]() and
and
![]() .
.
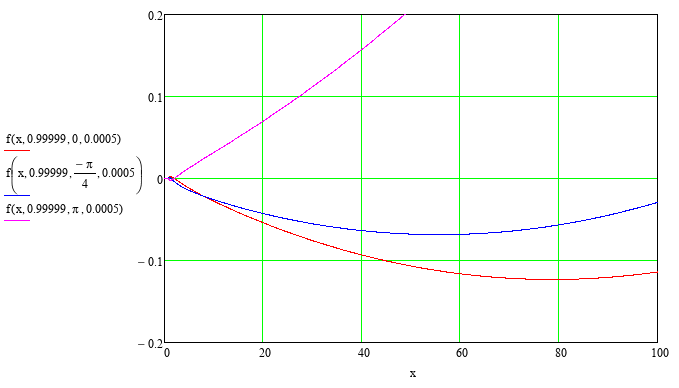
Examples
of frequency functions
![]() at various parameters
at various parameters
![]() ,
and both low values of
,
and both low values of
![]() are shown in Figure
11.
are shown in Figure
11.

Figure
11.
Frequency
functions
![]() at low values of argument
at low values of argument
![]() ;
relative amplitude of fluctuations of FFA
;
relative amplitude of fluctuations of FFA
![]() .
.
Examples
of frequency functions
![]() at various parameters
at various parameters
![]() ,
and both low (a) and high (b) values of
,
and both low (a) and high (b) values of
![]() are shown in Figure
12
and
Figure 13 a,b.
are shown in Figure
12
and
Figure 13 a,b.
Figure
12.
Examples
of frequency functions
![]() at high values of argument
at high values of argument
![]() ;
relative amplitude of fluctuations of FFA
;
relative amplitude of fluctuations of FFA
![]() .
.
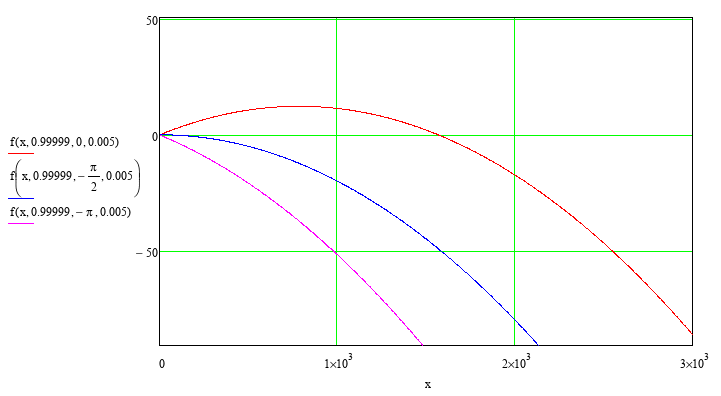
a.
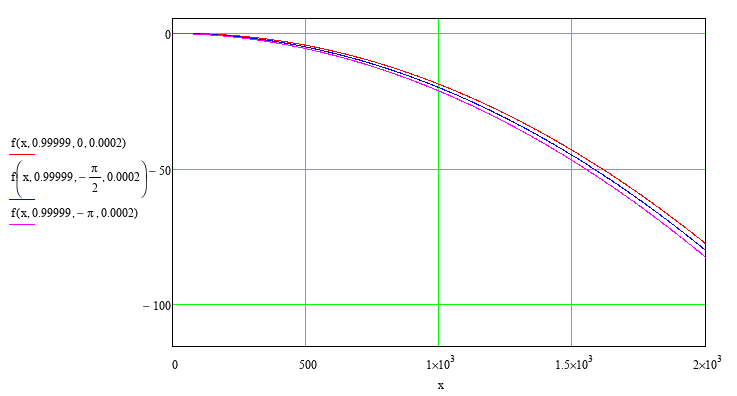
b.
Figure
13.
Examples
of frequency functions
![]() at the high values of argument
at the high values of argument
![]() ;
à.
- relative amplitude of FFA fluctuations
;
à.
- relative amplitude of FFA fluctuations
![]() ,
b. -
,
b. -
![]() .
.
Obviously,
the sign and a general view of functions
![]() essentially
depend on parameters
essentially
depend on parameters
![]() .
According to estimations given above, in the calculations,
.
According to estimations given above, in the calculations,
![]() is assumed. The given calculated dependences show that even at
small, with relative value of about the 100-th fractions of percent,
amplitudes
is assumed. The given calculated dependences show that even at
small, with relative value of about the 100-th fractions of percent,
amplitudes
![]() of fluctuations in value of normal acceleration of the gravity of the
Earth, the weight of mechanical oscillator can be changed
appreciably.
of fluctuations in value of normal acceleration of the gravity of the
Earth, the weight of mechanical oscillator can be changed
appreciably.
At
frequencies
![]() of oscillations, with an order of the frequency
of oscillations, with an order of the frequency
![]() of own FFA fluctuations, in area
of own FFA fluctuations, in area
![]() ,
the weight of oscillator periodically changes with frequency, and
sign and values of such changes essentially depend on a difference of
phases
,
the weight of oscillator periodically changes with frequency, and
sign and values of such changes essentially depend on a difference of
phases
![]() of oscillations (see Figure
11).
At high (
of oscillations (see Figure
11).
At high (![]() )
frequencies of oscillator, the monotonous dependence of average
weight of oscillator on frequency of its fluctuations is taking
place, with influence of phase
)
frequencies of oscillator, the monotonous dependence of average
weight of oscillator on frequency of its fluctuations is taking
place, with influence of phase ![]() being insignificant (Figure
13. b).
Such
reduction of weight of oscillator at high frequencies of fluctuations
will agree with negative temperature dependence of weight of bodies
as the frequencies of thermal fluctuations of microparticles of solid
state bodies are rather high and lie in the field of the hypersound.
being insignificant (Figure
13. b).
Such
reduction of weight of oscillator at high frequencies of fluctuations
will agree with negative temperature dependence of weight of bodies
as the frequencies of thermal fluctuations of microparticles of solid
state bodies are rather high and lie in the field of the hypersound.
Obviously,
the sign and a general view of functions
![]() essentially
depend on parameters
essentially
depend on parameters
![]() .
According to estimations [7], in the calculations,
.
According to estimations [7], in the calculations,
![]() is assumed. The given calculated dependences show that even at
small, for example, with relative value of about the 100-th fractions
of percent, amplitudes
is assumed. The given calculated dependences show that even at
small, for example, with relative value of about the 100-th fractions
of percent, amplitudes
![]() of fluctuations in value of normal acceleration of the gravity of the
Earth, the weight of mechanical oscillator can be changed
appreciably.
of fluctuations in value of normal acceleration of the gravity of the
Earth, the weight of mechanical oscillator can be changed
appreciably.
At
frequencies
![]() of
oscillations, with an order of the frequency
of
oscillations, with an order of the frequency
![]() of own fluctuations of FFA, in area
of own fluctuations of FFA, in area
![]() ,
the weight of oscillator periodically changes
with
sign and values of such changes essentially depending on a difference
of phases
,
the weight of oscillator periodically changes
with
sign and values of such changes essentially depending on a difference
of phases
![]() of oscillations and FFA (Figure
11).
of oscillations and FFA (Figure
11).
6. Experimental Dependence of Acceleration of Free Falling Rotor
Experimental check of the dependence of average weight of the above-considered oscillator on frequency of its fluctuations can be executed, measuring the instant values of acceleration of free falling rotor [11]. Mechanical rotor is the system of the accelerated, moving on a circular trajectory microparticles, forming a solid state body, and linked to each other by forces of elasticity. With horizontal orientation of rotor rotation axis, the vertical component of trajectories of movement of particles of the rotor corresponds to the oscillations of such particles considered in [3,7].
Measurements of instant values of free falling acceleration of the closed container with the rotor of vacuum mechanical gyroscope fixed inside are described in [11,15]. The rotor (mass is 250 g ) gathered momentum up to the maximal frequency 400 Hz , then during the run out time (about 22 min) its frequency smoothly decreased, the container was periodically dropped down, and by method of falling scale, the instant values of acceleration of free falling of the container were measured. The example the frequency dependence of change of acceleration of free falling container with a rotor fixed inside it, and with horizontally positioned axis of rotor is shown in Figure 14.
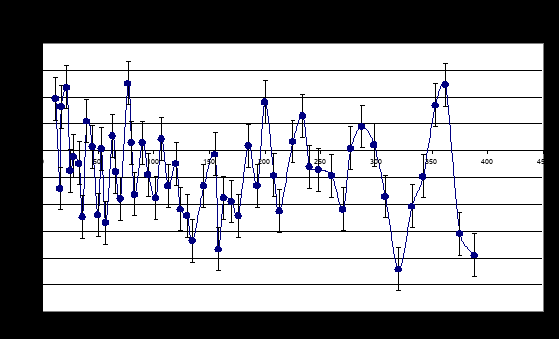
Figure 14. The frequency dependence of free falling acceleration of the container with horizontally positioned rotor; the changes of AFF ( Gal ) relatively to the value of AFF with the stopped rotor have been shown.
Experimental researches into free falling mechanical oscillators (rotors, vibrators) will allow to bring the necessary specifications into the offered models, to determine the borders of their applicability, and to prove more strictly the size parameters introduced into these models. Such researches will promote obtaining the new data on dynamic characteristics and specific features of the gravitational field of the Earth.
7. Orbital space experiment
Laboratory
measurements of effect of temperature on the force of gravity were
conducted with thorough consideration of the effect of different
disturbances (thermal expansion of bodies, Archimedean force, air
convection, electric and magnetic fields, etc.). Experimental error
of the value of temperature coefficient
![]() was
approximately several ones to dozen %. High accuracy of measurements
of temperature dependence of the force of gravity may be achieved in
proposed space experiment. In essence such experiment proposes to fix
position of heated sample body being placed in the orbit of Earth
satellite [15,16].
was
approximately several ones to dozen %. High accuracy of measurements
of temperature dependence of the force of gravity may be achieved in
proposed space experiment. In essence such experiment proposes to fix
position of heated sample body being placed in the orbit of Earth
satellite [15,16].
With
constant velocity of the orbital movement of the body, changes
![]() of acceleration of gravity applied to the body correlated to the
change
of acceleration of gravity applied to the body correlated to the
change
![]() of its gravitational (inert) mass, cause proportional changes
of its gravitational (inert) mass, cause proportional changes
![]() of the radius of its orbit,
of the radius of its orbit,
![]() .
(17)
.
(17)
According
to (1), with positive
![]() , heating of the body
, heating of the body
![]() will affect decrease
will affect decrease
![]() of the radius of its geocentric orbit. Specifically in relative
approximation
of the radius of its geocentric orbit. Specifically in relative
approximation
![]() .
(18)
.
(18)
If
on near Earth orbit across its radius there are two bodies and the
temperature of one of the bodies changes, physical temperature
dependence of the force of gravity (free fall acceleration) will be
the cause of the change of relative position of such bodies. With
carrier radius close to average radius of Earth
![]() ,
relative radial offset of the sample, i.e. heated to 1000
C, is equal to about
,
relative radial offset of the sample, i.e. heated to 1000
C, is equal to about
![]() .
For higher orbits temperature shift
.
For higher orbits temperature shift
![]() of the weight increases. Modern sensors measure shift of surfaces
much lower than stated value (fractions of nanometers).
of the weight increases. Modern sensors measure shift of surfaces
much lower than stated value (fractions of nanometers).
Principal scheme of measuring module is shown on Figure 15.
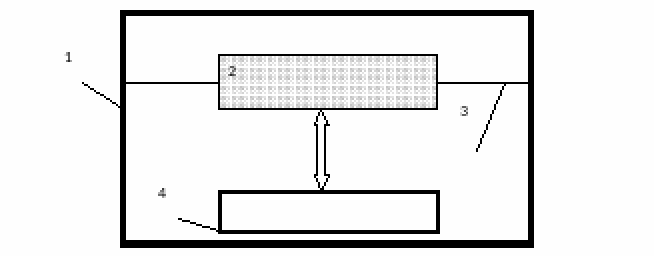
Figure 15. The device of the measuring system. 1 - case; 2 - test mass with electric heater; 3 - membrane spring; 4 - displacement meter
Space
method of measurements will allow to determine the value of
temperature coefficient
![]() of the weight change with precision higher than
of the weight change with precision higher than
![]() ,
which is enough for measurement of both relative and non-relative
effects.
,
which is enough for measurement of both relative and non-relative
effects.
Conclusion
Temperature dependence of the force of gravity is still an object of scientific discussions. High precision terrestrial and space experiments in this area will clarify the problem. They will accelerate progress of both physics of gravity and its practical applications.
References
Shaw P. E. and Davy N. The Effect of Temperature on Gravitative Attraction, (1923) Phys. Rev. V. 21(6), pp. 680-691.
Dmitriev A. Temperature Dependence of Gravitational Force: Experiments, Astrophysics, Perspectives. arXiv: physics/0611173, 20 Nov. 2006.
Dmitriev A. L., Nikushchenko E. M. and Snegov V. S. Influence of the Temperature of a Body on its Weight, (2003) Measurement Techniques, V. 46, No 2, pp. 115-120.
Dmitriev A. L., Experimental Study of Gravity Force Temperature Dependence (2007), 8-th International Conference of General Relativity and Gravitation (GRG-18), Sydney, Abstract Book, pp. 77-78.
Fan Liangzao, Feng Jinsong, Liu Wuqing, An experiment discovery about gravitational force changes in materials due to temperature variation, (2010) Engineering Sciences (China), ¹ 8 (2).
Rocklein M. N., George S. M., Temperature-Induced Apparent Mass Changes Observed during Quartz Crystal Microbalance Measurements of Atomic Layer Deposition, (2003) Analytical Chemistry. V 75. ¹ 19. pp. 4975-4982.
Dmitriev A. L., Bulgakova S. A. Negative Temperature Dependence of Gravity – A Reality, (2013) Proc. WASET. Issue 79. pp. 1560-1565.
Dmitriev A. L., Thermogravimetry and the negative temperature dependence of gravity, (2015) Applied Physics Research, V. 7, No 6, pp. 43-48.
Wendlandt, W. Thermal Methods of Analysis, John Wiley & Sons, New York, 1974.
Dmitriev, A. L. Physical substantiation of an opportunity of artificial change of body weight, Physics Procedia, 2012, Vol. 38, pp. 150-163.
Dmitriev A. L. Prospects of high-frequency gravimetry. Proc. of the International Conference APSAC 2015, Vienna, Austria, March 15-17, 2015. pp 237 – 240. International Journal of Circuits, Systems and Signal Processing. Vol. 9. pp. 275-280 (2015).
Dmitriev A. L., Chesnokov N. N., Reduction of the weight of optical fiber during distribution of laser radiation, (2018) Proc. VII International Conference on Photonics and Information Optics, Moscow, pp. 224-227.
Dmitriev A. L., Nikushchenko E. M., On the Shape of the Glow Discharge Channel, (2017) Technical Physics, V. 62, No. 5, pp. 816–817.
Dmitriev A. L., Nikushchenko E. M., Expulsion of Plasma in a Gravitational Field, (2016) Applied Physics Research, V. 8, No 2, pp. 38-39.
Dmitriev A. L., Physical Gravity (2018), “Pechatnyj Ceh.” Publ., SPb, 240 p.
Dmitriev A. L., in Proc. XII All-Russ. Conference “Innovation Techn.”, V. 1, pp. 64-67, SPb (2020).