Keywords—Gravitation, temperature, weight.
By the papers in the most authoritative scientific journals, the last experimental work dealing with research of temperature dependence on the force of gravitation was published in 1923 by Shaw and Davy in Phys. Rev. [1]. For the next 80 years interest to this theme had considerably fallen that was promoted much by the statement which had been made within the general theory of relativity regarding the smallest and practically not observable positive temperature dependence of physical weight of bodies. Meanwhile, a careful analysis of experimental data of Shaw and Davy shows that even those authors actually observed appreciable negative temperature dependence of force of gravitation [2].
At the beginning of the 21st century some works of the Russian and Chinese researchers showing rather strong negative influence of temperature on weight of bodies [3-6] became known. Nevertheless, the enormous reputation of the general theory of relativity till now sets barriers to the organization of experimental researches of temperature dependence of gravitation.
Actually, negative temperature dependence of force of gravitation directly contradicts the general theory of relativity and, in particular, puts under doubt a reality of achievement of a singularity condition at a gravitational collapse; hence, it also forces to doubt some popular cosmological theories.
No matter how reasons of pure theorists were convincing, physics is primarily an experimental science and it is just experience that makes basis of adequate physical concepts.
The paper provides the results of recent laboratory experiment s regarding studying the influence of temperature on physical weight of bodies and considers some simple phenomenological models allowing to prove the obtained experimental data.
The results of measurements of mass of thermo-isolated containers containing heated up metal elements in which temperature reduction of weight is regularly observed and which can not be explained by the action of artefacts are submitted below.
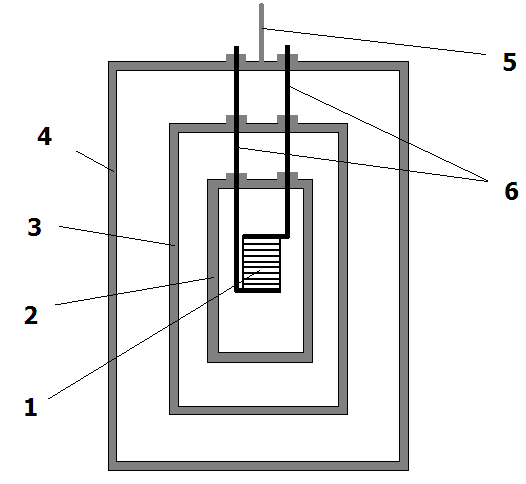
In the first series of measurements a copper sample which is placed inside a three-layer container was heated up before weighing by means of an electric spiral. The design of such container (No 1) is shown in Fig. 1.

Fig. 1 The design of container No 1. 1 - a copper sample with a winding of an electric heater; 2,3 - cylinders from titan; 4 - cylinder from brass; 5 - a wire of suspension bracket of container; 6 - copper conductors
Use of container in form of three enclosed tight metal cylinders with thickness of walls of 1.0 mm, two of which are made of titan - a material with low factor of heat conductivity, and the external cylinder - from brass, improves thermo-isolation properties of the container. The heated sample is a copper core 10 mm in diameter, height of 15 mm, weight of 10.3 g which is wrapped up with a layer of mica and an incandescence filament - Nichrome wire 0.3 mm in diameter.
Tightness of containers is provided by tight fit of cylinders covers and by "cold welding" of all elements of the joint, including electrodes of the heater. Weight of the collected container is 128 g, diameter of the external cylinder is 40 mm, height is 51 mm. Time of heating of a copper sample is 60 s, current in the circuit of the heater is 1.5 A, electric resistance of the heater is 6 Ohm. Under the specified conditions of the experiment the temperature of the external of a calibrated thermo-element.
After heating the container was weighed with laboratory scales of wall of the container was preliminarily measured by means XP2004S Precision trade mark by firm "Mettler-Toledo GmbH" under normal conditions of atmosphere in the working room (temperature of air is 240C, humidity - 45 %, pressure - 1000 hPa). Results of measurements of the current values of mass of the container and temperatures of its surface are given in Fig. 2. Here, there is also shown calculated according to temperature measurements change of weight of the container, caused by influence of air convection.
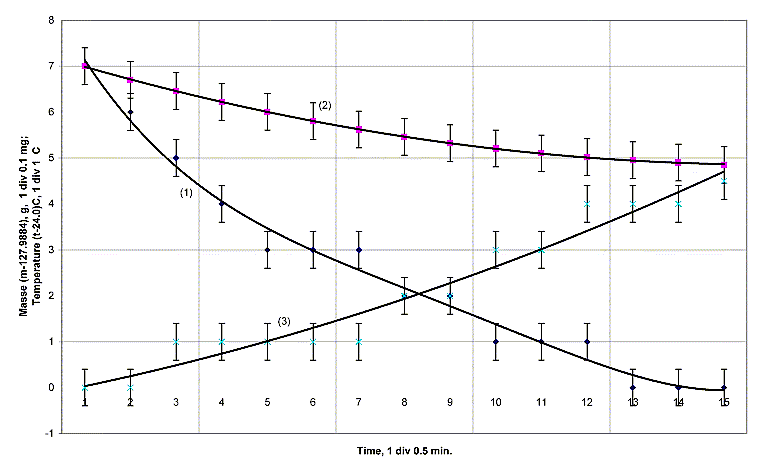
Fig. 2 1 - experimental time dependence of weight of container No 1; 2 - calculated dependence of weight of the container with account for influence of air temperature convection; 3 - change of temperature of surface of the external cylinder
The design of container No 2, with external cylinder made of steel, is shown in Fig. 3.
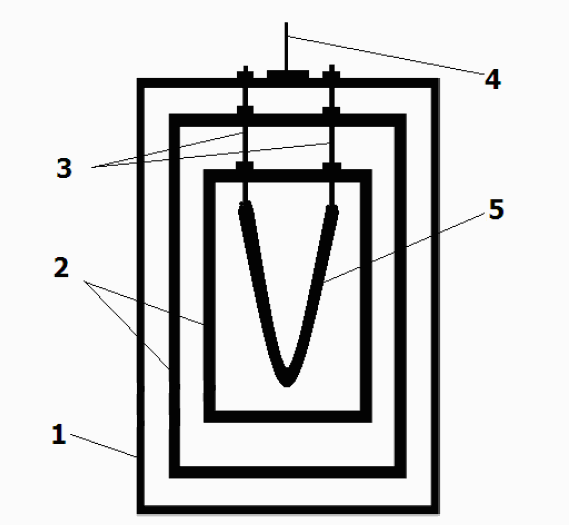
Fig. 3. The design of the container No 2. 1 - a cylinder made of steel, 2 - cylinder made of titan, 3 - copper electrodes, 4 - a suspension bracket, 5 - an electric spiral
Here as a heater, there is used a Nichrome spiral with weight of 540 mg, suspended inside the small cylinder. The full weight of the container is 167 g, thickness of walls of the external cylinder - 1.5 mm, diameter - 40 mm, height - 53 mm; thickness of walls of internal cylinders from titan - 2.0 mm. An electric heater with 10.5 Ohm resistance was connected to a power source (voltage 15 V, current 1.3
А) for 40 min, then the container was weighed. Results of measurements of mass of container No 2 and temperatures of the wall of the external cylinder are given in Fig. 4.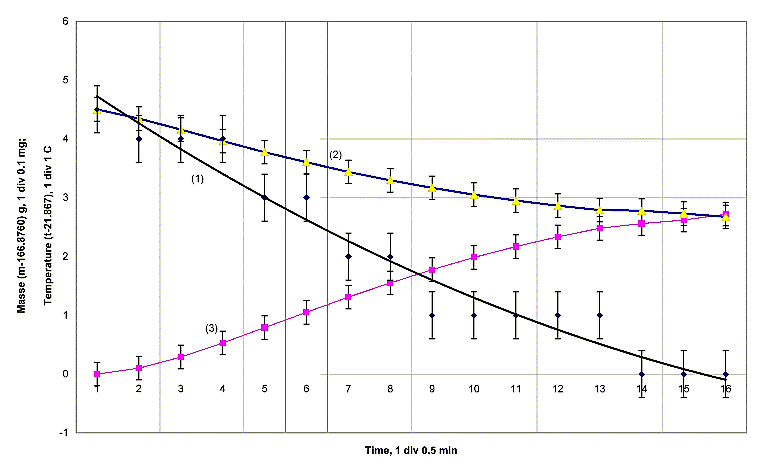
Fig. 4 1 - experimental time dependence of weight of container No 2; 2 - calculated dependence of weight of the container with account for the influence of temperature air convection; 3 - change of temperature of the surface of the external cylinder
The design of container No 3, in which heating of a tight steel cylinder made of stainless steel was carried out by a chemical method, is shown in Fig. 5.
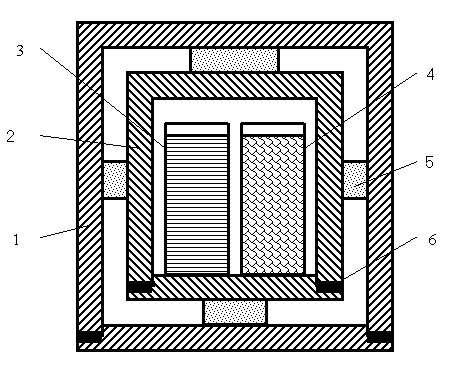
Fig. 5. The design of container No 3 with chemical heating of the internal cylinder. 1 - the external cylinder; 2 - the internal cylinder; 3 - an open vessel with distilled water; 4 - an open vessel with crystals of NaOH; 5 - polyfoam; 6 - vacuum sealing
Diameter of the external brass-cylinder is 60 mm, height - 62 mm, thickness of walls - 3.5 mm, weight - 475 g; diameter of the internal cylinder - 45 mm, height - 46 mm, thickness of walls -4.5 mm, weight - 280 g. In the condition specified in the figure the temperature of the internal cylinder is constant, the weight of completely equipped container is equal to 773.7651g.
Measurements of weight with a margin error readout of 0.1 mg were also carried out with laboratory scale of XP2004S mark at temperature of air in a working room equal to 19.8 0C, humidity - 31.8 %, pressure - 1022 hPa.
In the course of measurements the container was overturned, then the current value of its weight was registered. In the overturned condition, inside the small cylinder, there is going a process of partial dissolution of crystals NaOH (masse of 5 mg) in distilled water (masse of 6 mg) which is accompanied by heat release. The temperature of the mix in the first seconds of reaction grows by 10 0C, and, as have been shown by special measurements, the average temperature of the internal temperature of the mix in the first seconds of reaction grows by 10 0C, and, as have been shown by special measurements, the average temperature of the internal cylinder, owing to a heat transfer, is smoothly increased by 3-4 0C within the first two-three minutes. A specific feature of the given experiment is that, first, the process of dissolution of crystals of alkali is not accompanied by release of gases and, due to reliable sealing of covers of containers, the release of air from small and big cylinders (and the corresponding handicap to weighing) is absent. Second, due to the big weight of the external cylinder, the temperature of its surface, owing to a heat transfer, increases during the first two minutes by no more than by 0.2 0C. As a result, apparent reduction of weight of the container caused by air convection, which is determined by differences of temperatures of the surface of the container and the ambient air, in the first 2-3 minutes of measurements does not exceed 0.1 mg. High durability of the external cylinder also practically excludes influence of its weak temperature deformations on change of buoyancy of the weighed container.
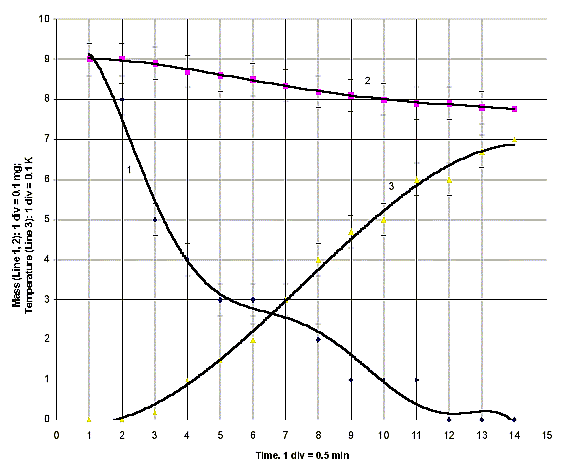
Fig. 6. 1 - experimental time dependence of change of weight of container No 3 in the overturned position; 2 - calculated dependence of change of weight of the container with account for influence of temperature air convection; 3 - experimental dependence of temperature of the surface of the external cylinder
Fig. 6 shows experimental time dependences of weight of container No 3, temperatures of its surface, and the calculated value of weight caused by temperature convection of air close to the walls of the container. Obviously, the paths of curves 1 and 2 essentially differ, accompanied by a typical sharp fall of weight of the container during the first minutes of measurements.
Let's estimate influence of temperature artefacts on the results of measurements of weights of samples [7].
Calculated Total (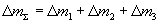 ) and Experimental (
) and Experimental (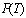 ) is Temperature Reduction of Weights of
Containers № 1-3
) is Temperature Reduction of Weights of
Containers № 1-3
|
№ |
|
|
|
|
|
|
|
mcg |
mcg |
mcg |
ΔmΣ, mcg |
mcg |
|
1 |
40 |
51 |
1.5 |
18.9 |
0.36 |
9 |
1.4 |
6.0 |
|
107 |
|
440 |
|
2 |
40 |
53 |
1.3 |
11.9 |
0.30 |
20 |
1.0 |
2.8 |
|
86 |
|
225 |
|
3 |
60 |
62 |
3.5 |
18.9 |
0.36 |
9 |
0.22 |
2.6 |
|
54 |
|
640 |
Change 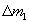 of apparent weight of the container, caused by change of volume of the steel cylinder owing to thermal expansion of its material is equal to
of apparent weight of the container, caused by change of volume of the steel cylinder owing to thermal expansion of its material is equal to
 (1)
(1)
where  - density of air,
- density of air, 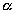 - factor of linear expansion of material of the cylinder,
- factor of linear expansion of material of the cylinder, 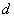 - its diameter,
- its diameter,  - height. Change
- height. Change  of apparent weight of the container, caused by deformations of walls of the cylindrical vessel, owing to temperature change of air pressure
of apparent weight of the container, caused by deformations of walls of the cylindrical vessel, owing to temperature change of air pressure 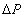 within its volume, as it is possible to show on the basis of the theory of elasticity [8], is equal to:
within its volume, as it is possible to show on the basis of the theory of elasticity [8], is equal to:
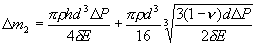 (2)
(2)
where  - thickness of walls,
- thickness of walls, 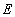 - the modulus of elasticity and
- the modulus of elasticity and 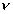 - Poisson's ratio . The size
- Poisson's ratio . The size 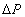
 is connected to change of temperature
is connected to change of temperature  of air within the volume of the external cylinder
of air within the volume of the external cylinder 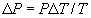 , where
, where 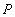 - normal pressure of atmosphere and
- normal pressure of atmosphere and 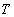 - temperature of air in the cylinder. The given estimate is overestimated, as in the second addend of formula 2, describing deformation of face walls of a vessel, such walls are presented by thin membranes; actually, the deflection of end faces is less than it is supposed in conclusion 2.
- temperature of air in the cylinder. The given estimate is overestimated, as in the second addend of formula 2, describing deformation of face walls of a vessel, such walls are presented by thin membranes; actually, the deflection of end faces is less than it is supposed in conclusion 2.
The change  of apparent weight of the container, caused by air convection due to difference
of apparent weight of the container, caused by air convection due to difference  of temperatures of surface of the external steel cylinder and temperatures of air in the closed box of analytical balance, will be estimated on the basis of [9] according to which
of temperatures of surface of the external steel cylinder and temperatures of air in the closed box of analytical balance, will be estimated on the basis of [9] according to which
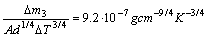 (3)
(3)
where the area of lateral surface of the cylinder is 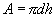 .
.
In Table I the experimental and calculated values of change of weights of containers No 1-3, corresponding to the third minute of measurements are given. In the given calculations the density of air 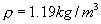 ,
, 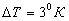 (obviously overestimated value),
(obviously overestimated value), 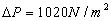 .
.
Obviously, observable (registered) reduction of weights of containers essentially, with account for errors of measurements, exceeds calculated one.
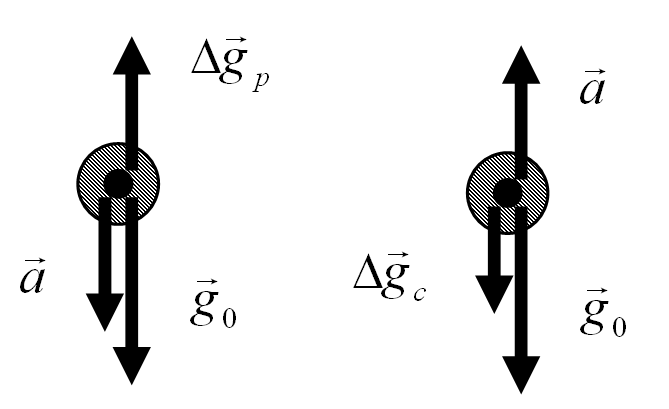
Let's consider the gravitational analogy of the phenomenon of Faraday electromagnetic induction and Lenz rules - Fig. 7 [10], [11].
(a) (b)
Fig. 7 Gravity analogy of the Faraday induction law and the Lenz rules
Proceeding from the principle of inertness of mechanical system, that is, its tendency to preserve the stable state, accelerated under action of external, for example, elastic force of movement of a test body downwards (Fig. 7 (a)) should cause an increment 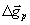 of acceleration of the gravity applied to a body which is directed from the centre of the Earth. On the contrary, the accelerated movement of a trial body upwards (Fig. 7b) is accompanied by increase of acceleration of the gravity applied to a body by value
of acceleration of the gravity applied to a body which is directed from the centre of the Earth. On the contrary, the accelerated movement of a trial body upwards (Fig. 7b) is accompanied by increase of acceleration of the gravity applied to a body by value 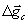 . Values
. Values 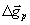 and
and 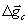 , generally speaking, can be different. Change of acceleration of the gravity acting on a body, moving with acceleration
, generally speaking, can be different. Change of acceleration of the gravity acting on a body, moving with acceleration 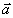 under influence of the elastic force, in the elementary (linear) approximation, is represented as
under influence of the elastic force, in the elementary (linear) approximation, is represented as
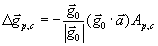 (4)
(4)
where symbols 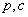 mean passing (
mean passing (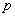 ) and a contrary (
) and a contrary (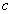 ), in relation to a direction of vector
), in relation to a direction of vector 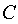 of normal acceleration of a gravity, orientation of a vertical projection of vector
of normal acceleration of a gravity, orientation of a vertical projection of vector 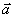 of acceleration of external forces, and factors
of acceleration of external forces, and factors 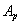 and
and 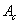 characterize a degree of change of values
characterize a degree of change of values 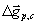 . If the massive body (for example, a ball) under action of the external, electromagnetic in nature, elastic force makes harmonious oscillations along a vertical with frequency
. If the massive body (for example, a ball) under action of the external, electromagnetic in nature, elastic force makes harmonious oscillations along a vertical with frequency 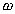 and amplitude
and amplitude 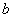 , the average for the period
, the average for the period 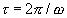 of fluctuations value
of fluctuations value 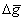 of change of acceleration of free falling (AFF) of such mechanical oscillator is equal to the sum of average changes of AFF in movement of a body passing and contrary to vector
of change of acceleration of free falling (AFF) of such mechanical oscillator is equal to the sum of average changes of AFF in movement of a body passing and contrary to vector 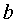 ,
,
 (5)
(5)
and at constant  it is equal
it is equal
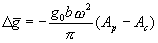 (6)
(6)
From (6), it follows that at 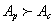 , the average acceleration of free falling of mechanical oscillator, for example, a rotor with a horizontal axis of rotation, is less than value
, the average acceleration of free falling of mechanical oscillator, for example, a rotor with a horizontal axis of rotation, is less than value 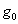 of normal acceleration of the gravity force. The reduction, averaged on several series of the measurements of the apparent weight of a rotor with horizontal axis, was observed in experiment [12], by results of which for the material of a rotor (stainless steel) it is possible to approximately estimate the order of value of difference
of normal acceleration of the gravity force. The reduction, averaged on several series of the measurements of the apparent weight of a rotor with horizontal axis, was observed in experiment [12], by results of which for the material of a rotor (stainless steel) it is possible to approximately estimate the order of value of difference 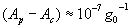 .
.
The absolute values of factors 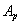 and
and 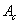 can be measured on the basis of the shock mechanical experiments accompanied by the high, above
can be measured on the basis of the shock mechanical experiments accompanied by the high, above 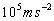 accelerations of interacting bodies. For steel samples the order of values
accelerations of interacting bodies. For steel samples the order of values 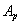 and
and 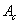 is approximately equal to
is approximately equal to 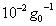 [13].
[13].
If to consider as the mentioned above trial body a microparticle of a solid body bound together by forces of interatomic interaction with other similar particles, formulas 1-3 allow to explain influence of temperature on acceleration of free falling (weight) of such body [4]. Thermal movement of microparticles of a solid body is accompanied by their significant accelerations, in so doing, the average value 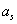 of a projection of these accelerations on a vertical is proportional to average speed of chaotic movement of microparticles. In a classical approximation, at a body temperature higher than the one of Debye-temperatures, the acceleration
of a projection of these accelerations on a vertical is proportional to average speed of chaotic movement of microparticles. In a classical approximation, at a body temperature higher than the one of Debye-temperatures, the acceleration 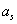 is in direct ratio to a square root from an absolute body temperature
is in direct ratio to a square root from an absolute body temperature 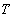 ,
,
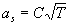 (7)
(7)
where 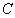 - the factor dependent on physical properties of a material.
- the factor dependent on physical properties of a material.
In one-dimensional approximation, we can consider a test body as a chain of microparticles bound by elastic forces, as shown in [3], [10],
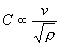 (8)
(8)
Where 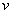 - speed of a longitudinal acoustic wave in a solid test body and
- speed of a longitudinal acoustic wave in a solid test body and 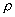 - its density.
- its density.
Formally, having replaced in equation (6) the average for the period of fluctuations magnitude of acceleration 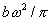 with average acceleration of particles
with average acceleration of particles 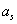 , we shall present the temperature dependence
, we shall present the temperature dependence 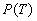 of weight of a body as
of weight of a body as
 (9)
(9)
where 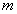 weight of a body,
weight of a body, 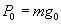 ,
, 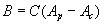 .
.
In a small range of temperatures the linear dependence of changes 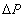 of weight and
of weight and 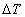 of a body temperature is satisfied,
of a body temperature is satisfied,
 (10)
(10)
Negative temperature dependence of weight of not-magnetic metal samples at close to normal (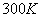 ) temperatures of bodies experimentally proves to be true, in so doing, the relative change of weight for a unit of temperature
) temperatures of bodies experimentally proves to be true, in so doing, the relative change of weight for a unit of temperature
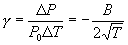 (11)
(11)
is equal to several units  [4].
[4].
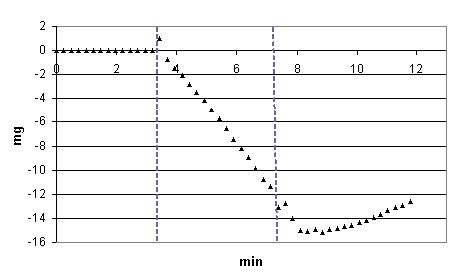
Fig. 8 Change in time of apparent weight of the metal core which is heated up with an ultrasonic radiator
The typical increase of value  along with reduction of density of a sample material is observed that is in agreement with (8) (see Table II). (We should note that outside the limits of considered classical approximation, for example, at close to zero absolute temperatures of bodies, formulas 7-8 are not satisfied).
along with reduction of density of a sample material is observed that is in agreement with (8) (see Table II). (We should note that outside the limits of considered classical approximation, for example, at close to zero absolute temperatures of bodies, formulas 7-8 are not satisfied).
Characteristics of Samples and Results of Measurement [4]
|
Sample |
Lead |
Copper |
Brass |
Titanium |
Duralumin |
|
Length, mm |
80.2 |
71.6 |
140.0 |
140.0 |
140.0 |
|
Diameter, mm |
8.0 |
10.5 |
8.0 |
8.0 |
8.0 |
|
Mass, g |
45.6 |
39.2 |
58.5 |
31.2 |
19.1 |
|
Ultrasound Frequency, kHz |
135.43 |
129.70 |
131.27 |
136.22 |
134.90 |
|
|
4.56 |
6.50 |
4.50 |
8.70 |
11.60 |
The magnitude of factor 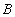 for the mentioned above materials is within the limits of
for the mentioned above materials is within the limits of 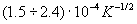 .
.
Strong calculation of time change of weight of the container containing a heater, is based on the decision thermo-physical tasks about distribution of heat to elements of its design. Owing to necessity of the account of boundary conditions and various physical properties of materials, the decision of such task is carried out by computing methods. The general tendency of time change of weight of the container at the initial moments of time of weighing can be found at the decision of a simple task on distribution of heat in a homogeneous bar. The one-dimensional equation of heat conductivity for thermo-isolated a homogeneous bar looks like
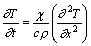 (12)
(12)
where  - function of distribution of temperature,
- function of distribution of temperature, 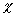 - factor of heat conductivity, c - a specific thermal capacity of a material of a bar,
- factor of heat conductivity, c - a specific thermal capacity of a material of a bar, 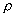 - density.
- density.
The example of temperature distribution on length of a bar in initial 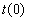 and the subsequent the moments of time are shown on Fig. 9.
and the subsequent the moments of time are shown on Fig. 9.
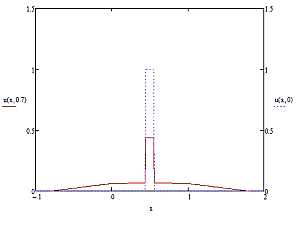
Fig. 9 Distribution of temperature (here - u) on length (x) of a bar in initial (a shaped line) and the subsequent (a continuous line) the moments of time
With the account (6), time dependence 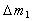 of weight of a bar in length
of weight of a bar in length 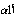 is represented by integral
is represented by integral
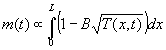 , (13)
, (13)
The example of settlement dependence 
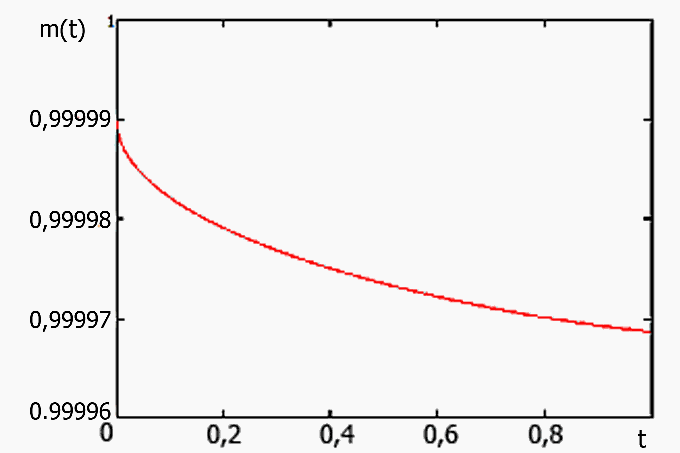
Fig. 10 Time dependence 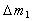 full weight of a homogeneous bar (in relative units)
full weight of a homogeneous bar (in relative units)
Apparently from this figure, for the initial moments of process of distribution of heat typically sharp reduction of weight of a bar. The similar tendency in experiments is observed that is especially appreciable on Fig. 2 and Fig. 6.
Temperature dependence of force of gravitation - one of fundamental problems of physics. The negative temperature dependence of weight of bodies is confirmed by laboratory experiments and similar to Faraday phenomenon in electrodynamics is a consequence of natural "conservatism" of physical system, its tendency to preserve a stable condition. Realization of experimental researches of influence of temperature of bodies on their gravitational interaction is timely and, undoubtedly, will promote progress of development of physics of gravitation and its applications. We welcome consolidation of efforts of various groups of researchers, both experimenters and theoreticians for implementation of this important problem.
Authors thank Yu. I. Kamenskih, V. S Snegov and E. M. Nikushchenko for the help in experiments, and Doctor of Chemistry I. B. Dmitrieva for recommendations regarding the choice of a chemical heater.
