The Clouds of Physics and Einstein's Last Query:
Can Quantum Mechanics be Derived
from General Relativity?
Prof. F. Winterberg, University of Nevada, Reno NV89557-0058
Abstract
Towards the end of the 19th century, Kelvin pronounced as the "clouds of physics", 1) the failure of the Michelson-Morely experiment to detect an ether wind, and 2) the violation of the classical mechanical equipartition theorem in statistical thermodynamics. And he believed that the removal of these clouds would bring physics to an end. But as we know, the removal of these clouds led to the two great breakthroughs of modern physics: 1) The theory of relativity, and 2) to quantum mechanics.
Towards the end of the 20th century more clouds of physics became apparent. They are 1) the riddle of quantum gravity, 2) the superluminal quantum correlations, and 3) the small cosmological constant. As there was in the discovery of radioactivity by Bequerel and Curie, really one more cloud of 19th century physics carried over to become a 20th century cloud of physics, leading to the discovery of the atomic nucleus (and nuclear energy), there are likewise late 20th century clouds which have become 21st century clouds of physics. They are: 1) The riddle of dark energy making up 70% of the physical universe, 2) the non-baryonic cold dark matter making up 26%, and 3) the very small initial entropy of the universe. It is the very small initial entropy which is most difficult to understand, with some scholars even suggesting for its explanation a divine intervention (see my version of Michelangelo). But with GOD normally not mentioned in physics textbooks, this has become an embarrassment for the physics community.
In my talk I will try to explain the importance of these clouds for the future of physics and present conjectures for a possible solution of these riddles. These conjectures will have to do with Einstein's last query: "Can quantum mechanics be derived from general relativity", and with the question is there an ether?
To create our universe GOD must aim at a point in phase space of the entire universe as small as 1/1010123
1. Introduction
One great scientific event of the 19th century was Darwin's theory of evolution. The theory made a lot of sense provided a sufficient amount of time was given. But as Kelvin, at his time a towering authority in physics, had pointed out (by the theory he and Helmholtz had developed), the sun could not be more than 100 million years old, explaining the radiative energy output by the sun to result from the conversion of gravitational potential energy into heat through its shrinking to a smaller diameter. The conclusion by Kelvin was a big blow to Darwin's theory, because it was difficult to believe that a time of 100 million years was long enough to explain the evolution from bacteria to homo sapiens. Today, of course, we know that the sun shines by the release of energy from nuclear fusion, giving it a lifetime of about 10 billion years, sufficiently long for Darwin's theory of evolution. This is a good example of how careful one should be in drawing such far reaching conclusions as were drawn by Kelvin, and as they are drawn today with our present (most likely still) limited knowledge of the physical universe. We are fairly certain, ordinary matter, of which we and all the stars are composed, makes up only 4% of the material content of the entire universe, with 26% made up from completely unknown heavy particles (the non-baryonic cold dark matter), and 70% of an unknown energy ("quintessence"), not even made up of particles.
At his time Kelvin tried to bring the house of physics in order, not only with regard to the time scale he gave for Darwin's theory of evolution. He was of the opinion that apart from a few "clouds", physics is an almost completed science. These clouds were: 1) The failure of the Michelson-Morely experiment to detect an ether wind, and 2) the failure of classical statistical thermodynamics to explain the specific heat of solids at low temperatures. As we know today the removal of these clouds led to the two great breakthroughs of 20th century physics: The theory of relativity and quantum mechanics. Adding the discovery of nuclear energy, not anticipated by Kelvin, there were three clouds in all.
At the turn from the 20th into the 21st century there again appear new clouds over the horizon, not less mystifying than were Kelvin's clouds. Drawing from Kelvin's experience, it is very unlikely that these clouds can be removed by the extrapolation of present theories, like the extrapolation of general relativity in the four space-time dimensions, (the dimension of every physics laboratory), to more than four space-time dimensions, and from zero-dimensional point particles to higher dimensional brane particles. What is mathernaticalfy so obvious, as are these extrapolations, is physically most likely wrong. We must rather look for radical new ideas, such as suggested by Einstein's last query: "Can quantum mechanics be derived from general relativity?" In paraphrasing Bohr (with regard to Heisenberg's failed unified field theory), it is not that at first glance this question seems to be crazy, but if it is crazy enough to be true.
2. The New Clouds
At the turn of the 21st century, the most vexing cloud of physics was and still is the unsolved problem of quantum gravity: How to quantize Einstein's gravitational field equations. While of the four fundamental forces of nature, the electromagnetic, the weak, the strong, and the gravitational force, only the first three can be quantized in a mathematically consistent way, this turns out to be impossible for gravity. The problem seemed to be solvable only by making such outlandish conjectures that there are more than the three dimensions of space, and that the point-like structure of elementary particles, (required by the postulates of the special theory of relativity), must be replaced by strings or higher dimensional surfaces (membranes). In making the second of these two conjectures, the followers of this line of research seem to have forgotten that points, lines, and surfaces are just abstract elements of Euclidean geometry with no physical meaning. The argument in favor of strings is that the infinities in relativistic quantum mechanical calculations can there be avoided. But because of Heisenberg's uncertainty relation, to measure the zero diameter of a string or thickness of a membrane requires an infinite amount of energy, this avoidance is an illusion. For point-like particles, quantization works only for renormalizable theories, like quantum electrodynamics, where the subtraction of two infinities is set equal to the value of an observed quantity. This "trick" does not work for quantum gravity.
While for quantum gravity the problem is "mathematical", it is for the superluminal quantum correlation (EPR experiment) "physical". About this problem, i.e. cloud of physics, countless papers and books have been written, making all sorts of philosophical conjectures, with the most outlandish the "many worlds interpretation". It is my belief that the reason for the failure of all these authors to reach a reasonable explanation for these superluminal connections is that they have put themselves into a "straight jacket" which can be expressed by the formula: Einstein can not be wrong and there are no superluminal connections. But the experiments, taken at face value, clearly demonstrate the existence of such superluminal connections. The easiest way to explain these superluminal connections is that there is an ether, which in addition to the transmission of electromagnetic and gravitational waves, permits the transmission of superluminal signals. But if there is an ether, it also can lead to a solution of the problem of quantum gravity, which is much more plausible than one assuming the existence of higher dimensions. As it was shown before Einstein by Lorenz and Poincare, the special theory of relativity can be completely and consistently derived from the existence of an ether. And with the superluminal quantum correlations, exposing themselves in such a clear case, as in Aspect's EPR experiment, there should be the possibility to detect the ether by experiment.
Two other clouds of the 21st century physics, the non-baryonic cold dark matter, and the dark energy making up 70% of the physical universe, also point in the direction for the existence of an ether.
We finally turn to the two remaining clouds, the small cosmological constant and the very small initial entropy. As it appears, they may be connected to each other. As I will argue, both of them suggest the hidden existence of negative, apart from positive masses. Assuming that there is an ether, these negative masses must be an essential part of this ether.
3. Einstein's Last Query
It is in seeking an answer to Einstein's last query: "Can quantum mechanics be derived from general relativity?" where we may find a key for the solution of all these mysteries, removing the last clouds of physics. On a first glance, Einstein's query seems to be absurd: How can quantum mechanics be derived from a classical field theory? But we must keep in mind that Einstein's field equations are not only nonlinear, but self-sourced. Classical fluid dynamics is also nonlinear but not self-sourced. Self-sourced means here, that the gravitational field, having energy and hence mass, is a source of its own field.
This then raises the question: Does one really need in addition to Einstein's vacuum field equation
|
Rik = 0 | (1) |
the geodetic equation of motion for a point mass singularity
In 1927 Einstein and Grommer [1] tried solve this problem, which they were able to find in the limit of weak fields. It turned out that in this limit they obtained the classical Newtonian equation of motion of a point particle, and the answer to Einstein's query seemed to be negative. However, the conclusion drawn was only valid under the restriction that the singularity is a mass monopole. This opens the question if something like quantum mechanics can be obtained admitting mass multipoles, containing negative masses, in particular mass dipoles, including the superposition of a mass monopole with a mass dipole (pole-dipole particle). One of the characteristics of quantum mechanics is the "Zitterbewegung" (quivering motion) of a particle. It was shown by Mathisson [2] and by von Weyssenhoff [3], that the motion of a more general mass multipole, strikingly resembles the quivering motion of an elementary particle, first derived by Schrodinger [4] in his famous papers on the "Zitterbewegung" for a Dirac particle. And as neither the quantum potential, derived from Schrodinger's equation, obeys the equivalence principle, nor does the motion of a mass multipole. This, of course, can not explain all of quantum, mechanics, but it is a hint that the existence of negative masses may play an important part in the fundamental laws of nature.
A second important characteristic of quantum mechanics is the superluminal wave function collapse, and a third characteristic is the wave function entanglement.
Entanglement actually already occurs in classical mechanics in the interaction of coupled harmonic oscillators. It there means that an assembly of such oscillators can be decomposed in a set of uncoupled oscillators (normal modes) by a principal axis transformation. Therefore, if as Schrodinger believed, the behavior of a single particle can be described by a wave equation, it can for two particles be described by a set of different quasiparticles (normal modes), each of them described by a wave function not entangled by the wave function of the other quasiparticle. This description, however, requires to give up the particle aspect entirely, viewing particles not more than the normal modes of an ether. Giving up the multi-particle aspect and replacing it by a set of normal modes in an ether means that the particles can not be localized, because they are spread out over space, as are waves. The particle property then only emerges if a measurement is made, by which the wave function collapses into small volumes of space, giving the appearance of a particle, for example on a spot of a photographic plate. The question then comes up: What causes the collapse of the wave function? I offer the following conjecture as an answer: It is a kind of gravitational collapse, on the time scale (G Newton's constant)
where p is the density of the fluctuating ether.
If the special theory of relativity is considered a dynamic ether theory, with electromagnetic and gravitational waves moving with the velocity of light through an ether, as in the pre-Einstein theory of relativity by Lorentz and Poincare, then the velocity of light can be surpassed during a gravitational collapse, where in reaching the event horizon, matter held together by electromagnetic or likewise acting forces, becomes unstable and disintegrates into more fundamental particles. According to our present view these ultimate particles can only be Planck mass particles. And in assuming that there are positive and negative masses, there must be positive and negative Planck mass particles. To be consistent with Planck's conjecture, that all of physics should be reduced to units named after him, the spatial extension of the Planck mass particles must be a Planck length.
4. The Planck Ether Hypothesis
To construct a model of the vacuum composed of positive and negative Planck mass particles, we assume that the vacuum is filled with an equal number of positive and negative Planck mass particles with each Planck length volume occupied in the average by one Planck mass particle. And to be consistent with Planck's hypothesis, these Planck mass particles must interact over a Planck length by the Planck force c4/G. We then only have to choose the sign of the force in such a way that the ether composed of positive and negative Planck mass particles is stable. This requires that the force between Planck mass particles of equal sign is repulsive, but between those of opposite sign attractive. While the law for the conservation of energy is conserved during the collision between a positive with negative Planck mass particle of mass mp, the momentum fluctuates by Ap = mpc. This behavior is illustrated on the cover and Fig. H.3 of my monograph (reference [5]) and reproduced here. Therefore, Heisenberg's uncertainty principle
where Ap = mpc, and Aq = rp (rp Planck length), is in the Planck ether established at the most fundamental scale, the Planck scale, solely from the hypothesis for the existence of negative masses.
A fluctuation of the momentum, of course, violates Newton's third axiom: actio = reactio. That Newton's third law is violated in quantum mechanics is also established in the sense that the wave function acts on the particle, but not the particle on the wave function.
|
Fig. 11.3 Diffusion of the positive and negative Planck mass fluid. Solid circles represent positive and dotted ones negative Planck mass particles |
5. The Quasipartirie Spectrum of the Planck Ether
The proposed Planck ether can be compared with a superfluid, but a superfluid with two mass components, and with the two components interacting in a way that the momentum fluctuates. As it turns out, this medium exhibits a spectrum of elementary particles, greatly resembling the spectrum of particles of the standard model.
Let us first make a comparison with the ground state spectrum of a superfluid, shown in Fig. III.6 of reference [5]. It is assumed that the spectrum of a superfluid is universal, with its shape taken from measurements of superfluid helium, with the Debye length replaced by the Planck length. In this spectrum the phonons (dilatons) are related to a scalar gravitational field, and the rotons can be identified with the particles of the non-baryonic cold dark matter. The rotons, with an energy somewhat below the Planck energy mpc2, are separated from the ground state by an energy gap, in fairly good agreement with the observation that 70% of the energy of the universe does not consist of particles, and that 26% consists of non-baryonic cold dark matter.
Next we are considering higher excitations of the Planck ether. As in a superfluid they result from quantized vortices. There are two such excitations, one in which the two superfluid components co-rotate, and one where they counter-rotate (see Fig III.4 of ref. [5])
The origin of charge is explained to result from a field of virtual phonons, having their source in the zero-point fluctuations of Planck mass particles bound in the vortex fragments, as shown in Fig. Ill 7 [5].
With no energy required for the excitation of a large number of positive and negative mass vortices, one obtains a lattice of vortex rings as shown in Fig. TV 2a [5], with two kinds of waves, shown in Fig. FV 2b [5], one simulating electromagnetic and the other one gravitational waves, both propagating with the velocity of light through this vortex lattice. This reduces the problem of quantum gravity (but also quantum electrodynamics) to a non-relativistic many body problem.
It was Schrodinger who showed that Dirac's equation implies the existence of negative masses, which by fonning a bound state with positive masses result in mass-pole-dipole configurations, possessing a luminal "Zitterbewegung". Instead, one can obtain the Dirac equation assuming the existence of negative masses. In the proposed Planck ether model, the Dirac spinors are quasiparticles made up from the positive and negative mass vortex solutions. And with the two kinds of vortex solutions, co- and counter-rotating, there are two families of Dirac spinors as in the standard model. Because the interaction between the vortices is nonlinear, there are no more than four such quasiparticle solutions as the four families of the standard model.
The masses of these Dirac spinor particles are explained by the positive gravitational interaction energy between a very large positive and a very large negative mass, the large positive and negative masses of the vortex quasiparticles, making up a Dirac spinor. The masses thusly obtained are in fairly good agreement with the empirical masses.
The model reproduces all of the symmetries of the standard model, replacing strings in higher dimensions with vortices in the three dimensions of space, and interpreting Lorentz invariance as a dynamic symmetry for objects held together by electromagnetic, or likewise acting forces.
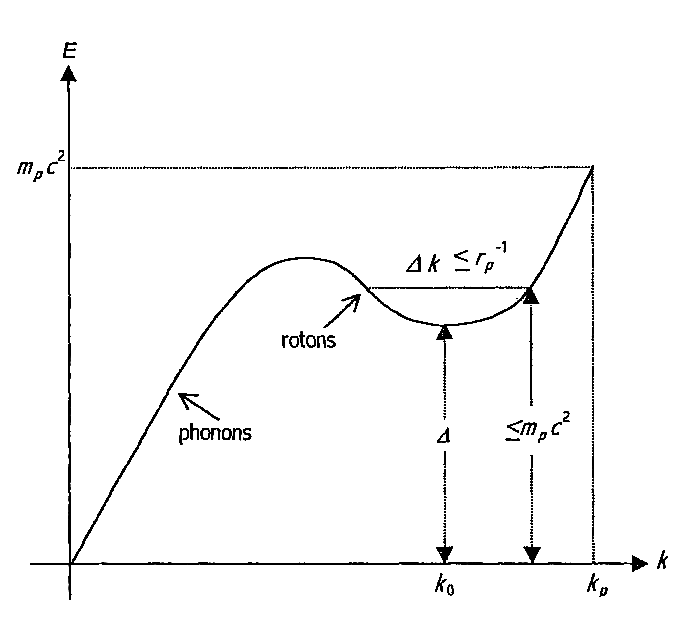
Fig. III.6 The phonon-roton energy spectrum of the hypothetical Planck aether
Fig. III.4 Row pattern of co- and counter-rotating vortex solutions.
Solid and dotted lines represent the flow of the positive and of the negative Planck mass fluid.
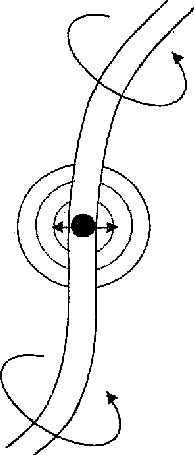
Fig. III.7 Origin of charge by zero point osciilations of Planck masses bound in vortex filaments generating a virtual field of phonons, resulting in a long range Newtonian gravitational force.
Electromagnetic wave
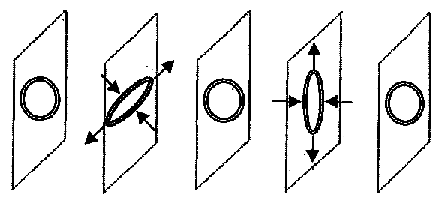
Gravitational wave
Fig. IV.2a The likely structure of the ring vortex lattice.
A dipping of a rectangular parallelepiped. The orientation of the rings is periodical.
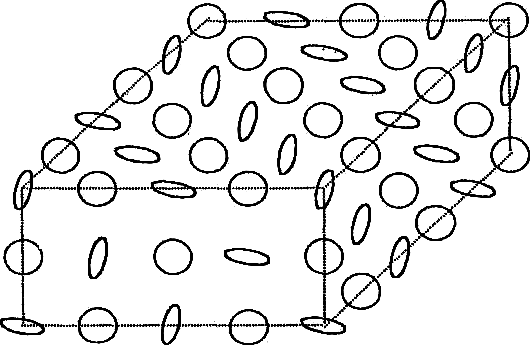
Fig. IV.2b Deformation of the vortex lattice for an electromagnetic and a gravitational wave.
6. The Problem of the Small Cosmological Constant and of the Small Initial Entropy
The assumption for the existence of hidden negative masses also sheds light on the two remaining mysteries: The small cosmological constant and the small initial entropy. Through the zero point energy of the vacuum, the cosmological constant A should be huge and of the order A = l/rp2, where rp = 10-33 cm is the Planck length, hence A = 1066 cm2. According to Einstein's gravitational field equations, this would mean that the radius of the universe is equal to R = rp ~= 10-33 cm. But astronomical observations rather suggest that R ~= 1028 cm. The cosmological constant is therefore off from what theory predicts by about 122 orders of magnitude. But if there is an equal number of positive besides negative Planck masses making up the Planck ether, both contributing by their mutual Zitterbewegung mechanism to the zero point energy of the vacuum, the cosmological constant would actually have to be zero. The observed small positive value of the cosmological constant can then possibly be explained by a dynamic symmetry breaking of the otherwise "symmetric" positive-negative mass ether.
The prospect to make plausible the smallness of the cosmological constant in the proposed positive-negative mass two-component ether model gives hope to make plausible the very small initial entropy of the universe [6], without invoking the help of God [5]. There we make the following hypothesis: If an assembly of positive and negative masses, with their total energy equal to zero, is brought together, the temperature and hence entropy of the mixture must go to zero. This hypothesis is the only one consistent with Nernst's theorem, which says that at zero temperature the entropy should be zero. To satisfy this hypothesis, we assume that negative masses have a negative entropy, because only then is an analytic continuation of the entropy from positive to negative temperatures possible.
For the entropy of a mixture of positive and negative masses to become zero in the course of a gravitational collapse requires an exact correlation in the disorder of the positive with the negative masses. This is certainly true if the negative mass is equal to the negative gravitational field energy of the positive mass, because the Newtonian gravitational field of each particle, all the way down to the smallest dimension, is precisely correlated to the position of the particle. The entropy of the positive mass of matter and the entropy of the negative mass of its gravitational field, might therefore be called complementary, like a positive and negative photographic image. Then, if in a gravitational collapse these two images exactly overlap, the entropy should go to zero. For the universe, the time needed to bring it back to a low entropy is the Poincare recurrence time. While under normal conditions this time is huge, it may in a dense mixture of positive and negative masses with a divergent acceleration become quite small.
Applied to the universe, this means that following its gravitational collapse, it can begin anew with a low entropy.
7. How Can We Detect the Ether?
All the talk about the existence of a hypothetical ether must remain empty unless we can find a way for its detection.
I will focus here on two possibilities:
To 1.
In terms of the wave number k, the spectrum of the quantum mechanical zero point vacuum energy is given by
|
f(k) = ћck3 |
(6) |
while the spectrum of turbulence goes as
|
F(k) = const.k-5/3 |
(7) |
It follows that for sufficiently small wave numbers (long wave lengths) the turbulence will overtake the zero point energy fluctuations, and it is not implausible to conjecture that in crossing this length, the quantum correlations in EPR type experiments begin to break down. To know more exactly at which wave length, the constant in (7) must be known. If it is determined by the observed departure of cosmic microwave background radiation from a Planckian distribution, this length turns out to be out of the order 100 km. Furthermore, if this length is different in different directions (against the stellar system, resp. ether rest frame), an absolute ether rest frame can be established, because unlike (6), (7) is not Lorentz invariant.
To 2.
With the wave function collapse conjectured to be some kind of gravitational collapse, it is conceivable that strong gravitational fields may influence the collapse, for example in the radioactive decay constant in probes brought near to the sun. Most of these highly interesting experiments should be done in the vacuum of space, using the solar system as a laboratory. This requires a nuclear propulsion system which permits to move large payloads with high velocities through the solar system. I therefore display an internet printout by some NASA space buffs, praising my idea how this could be done with a chain of exploding mini-nukes. I could think of no better way for mankind to get rid of its large arsenal of nuclear weapons in this way.
References
1. Электромагнитная волна (в религиозной терминологии релятивизма - "свет") имеет строго постоянную скорость 300 тыс.км/с, абсурдно не отсчитываемую ни от чего. Реально ЭМ-волны имеют разную скорость в веществе (например, ~200 тыс км/с в стекле и ~3 млн. км/с в поверхностных слоях металлов, разную скорость в эфире (см. статью "Температура эфира и красные смещения"), разную скорость для разных частот (см. статью "О скорости ЭМ-волн")
2. В релятивизме "свет" есть мифическое явление само по себе, а не физическая волна, являющаяся волнением определенной физической среды. Релятивистский "свет" - это волнение ничего в ничем. У него нет среды-носителя колебаний.
3. В релятивизме возможны манипуляции со временем (замедление), поэтому там нарушаются основополагающие для любой науки принцип причинности и принцип строгой логичности. В релятивизме при скорости света время останавливается (поэтому в нем абсурдно говорить о частоте фотона). В релятивизме возможны такие насилия над разумом, как утверждение о взаимном превышении возраста близнецов, движущихся с субсветовой скоростью, и прочие издевательства над логикой, присущие любой религии.
4. В гравитационном релятивизме (ОТО) вопреки наблюдаемым фактам утверждается об угловом отклонении ЭМ-волн в пустом пространстве под действием гравитации. Однако астрономам известно, что свет от затменных двойных звезд не подвержен такому отклонению, а те "подтверждающие теорию Эйнштейна факты", которые якобы наблюдались А. Эддингтоном в 1919 году в отношении Солнца, являются фальсификацией. Подробнее читайте в FAQ по эфирной физике.
|
|
 |
