|
|
|
|
|
|
|
|
|
|
|
На втором этапе эксперимент усложнялся: было сделано не по одному извлечению карточек из каждой пачки, а последовательно по 10 извлечений 30 раз, или 30 выборок. Сделав 10 извлечений по одной карточке из каждой пачки (извлекалась одна карта, возвращалась в пачку, пачка перемешивалась, и т.д.), подсчитав общую сумму номеров вынутых карточек (526) и разделив на 10, получили среднюю сумму 52,6. Так повторили 30 раз (табл. 3).
|
|
|
|
|
|
|
|
|
|
|
При проведении третьего этапа эксперимента в каждую из таких 30 случайных выборок входило уже по 40 извлечений. Среднее число из первых 40 извлечений составило 54,6, из вторых – 51,6 и т.д. (табл. 4).
|
|
|
|
|
|
|
|
|
|
|
Полученные эмпирические вероятности сравнивались с теоретической вероятностью. Последняя в данном примере равна средней сумме номеров десяти карточек в пачке, которая представляет собой как бы среднюю в исходной совокупности. Она равняется: 
. По значению отклонений от этой средней можно судить, насколько эмпирическая вероятность приближается к теоретической.
Размах колебаний индивидуальных сумм (указанных в табл. 2) был самым большим и равнялся 36. Это не что иное, как разность между максимальной и минимальной суммой (они в таблицах выделены и подчеркнуты). В табл. 2 максимальная сумма равнялась 72, минимальная 36 
. Отклонение этих показателей от средней (55) было наибольшим: 
и 
.
При выборках, состоящих каждая из 10 извлечений (см. табл. 3), размах колебаний уменьшился более чем вдвое, до 15,8 
, а максимальные отклонения от средней составили: 
и 
.
В выборках, состоящих каждая из 40 извлечений, размах колебаний по сравнению с результатами первой части эксперимента уменьшился более чем в 6 раз, составив только 5,8 
. Максимальные отклонения от средней равнялись при этом: 
и 
.
Распределение выборочных сумм отражено на графике рис. 1, на оси абсцисс которого отложены суммы выборки с указанием средней (55) в исходной совокупности, а на оси ординат – этапы эксперимента.
Результаты эксперимента показывают, что чем больше извлечений, тем их усредненные показатели плотнее группируются вокруг средней (теоретической вероятности) в исходной совокупности. То есть чем больше явлений изучено, тем надежнее полученные данные, тем точнее выявленные закономерности. Данный вывод – краеугольный камень всех статистических выборочных исследований.
Теоретические основы выборочного метода были бы неполными, если бы мы не коснулись законов распределения случайных величин, к которым подвел нас проведенный эксперимент.
Поскольку за внешними случайными явлениями стоят скрытые законы, то данные, характеризующие эти явления, должны распределяться определенным образом. Исходя из закона больших чисел, чем больше изученная совокупность случайных явлений, тем должно быть более упорядоченным распределение полученных данных. Обратимся к результатам различных этапов эксперимента. Из табл. 2-4 и рис. 1 видно, что на первом этапе эксперимента при 30 индивидуальных извлечениях числовые значения вынутых карточек, имея большое рассеяние, все же группировались вокруг средней суммы, равной 55. На втором этапе при 30 выборках по 10 извлечений эта тенденция стала более явной, а на третьем этапе при 30 выборках по 40 извлечений – очевидной.
Представим данные табл. 4 в виде вариационного ряда, ранжировав их от меньшего к большему по значению извлеченных карточек (табл. 5). Данные для простоты исчисления округлены до целых чисел.
|
|
|
|
|
|
|
|
|
|
Сумма |
Сумма |
Из табл. 5 видно, что с увеличением варьирующего признака (усредненной суммы значения карточек) частота извлечения этих сумм вначале увеличивается, а затем, после достижения максимального значения (
), уменьшается. Налицо закономерность. Упорядоченность изменения частот в вариационных рядах именуется закономерностью распределения. Данные табл. 5, изображенные графически в виде столбиковой диаграммы, гистограммы, полигона распределения, представлены на рис. 1, 2, 3.
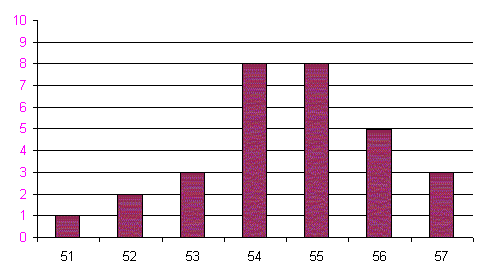
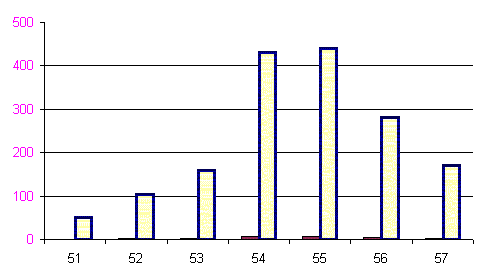
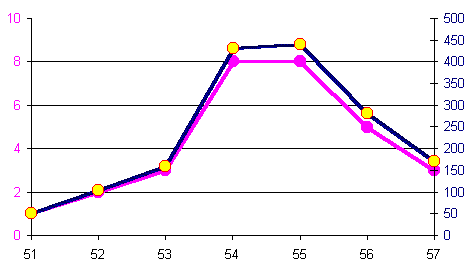
Гистограмма, или полигон распределения, представляет собой ломаную кривую, характеризующую фактическое распределение полученных данных. Она позволяет выявить лишь приближенную картину распределения всей (генеральной) совокупности. Чем больше выборочное изучение, тем в большей мере будут сглаживаться влияние случайных причин и явственнее будет проступать действительная закономерность распределения. В этом случае кривая распределения фактических данных будет приближаться к теоретической кривой распределения.
В математической статистике теоретическую кривую распределения обычно называют кривой Гаусса (Гауссовым распределением, нормальным законом распределения) (см. рис. 4).
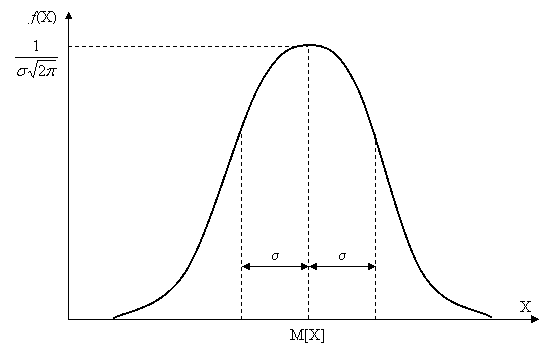
Нормальное распределение в чистом виде при выборочных исследованиях встречается часто, являясь своеобразным "атомом" или "квантом" многих сложных, то есть зависящих от нескольких независимых процессов распределений. При рассмотрении явлений, зависящих преимущественно от одной причины, их распределения окажутся близкими к нормальному. Если причин случайного процесса много, то его распределение имеет, как правило, много экстремумов. Если причина одна, то фактическое распределение выборочных показателей отличается от теоретического, главным образом, нарушением симметрии, т.е. если в нормальном распределении частоты анализируемого признака убывают по обе стороны от вершины кривой равномерно, то в фактическом распределении вершина кривой может быть смещена влево или вправо от теоретической средней, быть крутой с одной стороны и пологой – с другой (см. рис. 3). Причины таких смещений – малое число наблюдений, ошибки наблюдения и сбора данных.
Распределение показателей характеризуется размахом вариации и отклонением от средней.
Размах вариации (колебаний) – наиболее простой параметр измерения разброса значений варьирующего признака. Он исчисляется по формуле
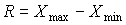
Наиболее полная характеристика распределения раскрывается через значение отклонения всех вариант от средней или значение отклонения эмпирических вариант от теоретических. Причем важно не столько отклонение каждой варианты от средней, сколько среднее отклонение всех вариант от средней, или дисперсия (колеблемость, пестрота) изучаемого признака. Упрощенно мы ее тоже рассчитывали. На первом этапе эксперимента значение отклонения от среднего находилось в диапазоне от +17 до –19, на втором – от +6,8 до –9, на третьем – от +2,3 до –3,5.
Средние величины – наиболее распространенные показатели в статистике. Это объясняется тем, что только с помощью средней можно охарактеризовать совокупность по количественно варьирующему признаку.
Средняя величина может раскрыть лишь общую тенденцию изучаемого явления и только тогда, когда она выведена из большого числа фактов и при изучении однородной совокупности. При несоблюдении этих условий средние показатели лишь введут в заблуждение. Примером может служить средняя заработная плата в нашей стране, когда в одну совокупность зачисляют и богатых, и бедных, разрыв в уровне обеспечения которых в 1997 г., например, составил соответственно 24:1.
В статистике разработано множество средних величин: степенные (средняя арифметическая, средняя гармоническая, средняя геометрическая и др.), мода и медиана. Каждая из средних выполняет свои аналитические функции. Для расчета дисперсии и других показателей выборочного наблюдения нам необходима лишь средняя арифметическая.
Среднее арифметическое – наиболее распространенный вид средних. Он используется в качестве центрального значения в рядах распределения и выполняет функцию теоретической вероятности. Все другие варианты расцениваются как случайные отклонения от него. Чем больше отклоняется какое-либо значение признака от среднего арифметического, тем более случайным оно является.
Средняя арифметическая простая, известная из школьных учебников по математике, рассчитывается по формуле
,
где 
, 
, 
,…, 
– значения признака; n – число значений.
При изучении больших совокупностей некоторые варианты имеют большие частоты повторения. Из табл. 5, например, видно, что варианта 52 повторяется дважды, 53 – трижды, 54 – восемь раз и т.д. В этом случае целесообразнее вначале каждую варианту умножить на частоту ее встречаемости, как это показано в графе (xf) упомянутой таблицы. Такое умножение в статистике называют взвешиванием. Средняя арифметическая в данном случае именуется взвешенной и рассчитывается по формуле
.
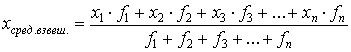Средняя арифметическая лежит в основе расчета дисперсии (колеблемости), которая представляет собой не что иное, как значение отклонения всех вариант от средней. Значение дисперсии и предопределяет объем выборочной совокупности. Чем больше дисперсия, тем больше разброс показателей от средней, а, следовательно, нужен больший объем выборки, чтобы она была достаточно репрезентативной. Репрезентативность (представительность) объема выборки практически не зависит от объема генеральной совокупности.
Расчет дисперсии качественных и количественных признаков неодинаков. Определение объема и представительности выборочной совокупности, а, следовательно, и дисперсии производится применительно не к каким-то явлениям вообще, а лишь к их конкретным показателям. Последние могут быть качественными, или атрибутивными, например, вид преступления, содержание мотива, свойства личности и т.д., и количественными (возраст людей в группе, уровень образования и дохода и т.п.). Каждый признак имеет свою дисперсию, а, следовательно, и необходимый объем выборки для надежного изучения. Это значит, что при выборочном изучении многих признаков, чтобы выявить совокупные отклонения, дисперсию надо рассчитывать по каждому из них. Иногда эти признаки исчисляются десятками и даже сотнями. Чтобы избежать множества расчетов, можно ограничить их только в отношении тех признаков, на базе которых делаются основные выводы. Общая численность выборки или ее общая репрезентативность определяются по совокупной представительности всех параметров.
. Расчет ее применительно к качественным признакам производится по одной формуле, а применительно к количественным - по другой.
Колеблемость качественного признака двухвариантна. В применении к статистике преступлений это: совершено преступление против собственности или иное, в состоянии опьянения правонарушителя или трезвым субъектом, по мотиву мести или иным побуждениям, лицом, воспитанным в неполной или полной семье, интровертом или экстравертом и т.д. Указанная двухвариантность отражается в таких относительных показателях, как удельный вес или доля признака в общей структуре изученных явлений, причин, событий, мер.
Удельные веса многих качественных признаков могут быть взяты из официальной статистической отчетности, которая основывается на сплошном текущем учете, из предыдущих исследований, достоверность результатов которых не вызывает сомнений, или других источников. Они могут быть специально получены на основе предварительного (пилотажного) изучения. Если удельный вес какого-то признака неизвестен и нет возможности получить его при предварительном изучении, то исследуемая совокупность по этому признаку условно принимается максимально неоднородной. В этом случае искомый удельный вес берется, равным 50% (или 0,5).
При наличии удельного веса качественного признака его дисперсия рассчитывается по следующей формуле: 
, где Р – доля качественного признака, а (
) – доля иных признаков или противоположного признака.
Дисперсия количественного признака многовариантна. Она рассчитывается с применением средней арифметической взвешенной (ее расчет приводился выше) по формуле
,
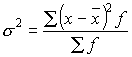где 
– дисперсия; х – показатели варьирующего признака; 
– среднее арифметическое значение признака; f – частоты вариант варьирующего признака.
Второй общепринятой мерой вариации признака является среднее квадратическое отклонение. Оно обозначается символом 
и выводится как самостоятельно, так и на основе среднего квадрата отклонений, т.е. дисперсии, которая обозначается .
Извлекая корень квадратный из дисперсии, получаем среднее квадратическое отклонение:
– для качественных признаков;
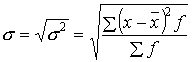– для количественных признаков.
Среднее квадратическое отклонение всегда выражается в тех именованных числах, в которых выражены варианта и средняя.
Очертания симметричной кривой нормального распределения полностью определяются двумя показателями – средней арифметической (х) и средним квадратическим отклонением (
). В зависимости от их значений она может иметь разный центр группировки показателей (рис. 4), быть более удлиненной, растянутой или сжатой, компактной (рис. 5).
На рис. 4 средняя арифметическая 
больше средней арифметической 
поэтому распределение II сдвинуто по оси абсцисс вправо. Средние квадратические отклонения распределений I и II одинаковы (
), следовательно, одинаковы и кривые распределения. На рис. 5, наоборот, средние арифметические (
) одинаковы, поэтому центры группировки обоих распределении на оси абсцисс совпадают, а среднее квадратическое отклонение распределения II (
) больше среднего квадратического отклонения (
), поэтому кривая II нормального распределения оказалась более растянутой, а кривая I – компактной.
Следующее свойство среднего квадратического отклонения позволяет правильно оценить надежность выборочных показателей. Если площадь, ограниченную кривой нормального распределения, принять за 1 или 100 %, то площадь, заключенная в пределах 1
вправо и влево от средней арифметической (рис. 6), составит 0,683 всей площади. Это означает, что 68,3% всех изученных вариант отклоняется от средней арифметической не более чем на 1
, т.е. находится в пределах (
).
Площадь, заключенная в пределах 2 вправо и влево от средней арифметической, составляет 0,954 всей площади, т.е. 95,4 % всех единиц совокупности находится в пределах (
). Площадь, заключенная в пределах 3 влево и вправо от средней арифметической, составляет 0,997 всей площади, или 99,7 % всех единиц совокупности находится в пределах (
). Это и есть так называемое правило трех сигм, характерное для нормального распределения.
При проведении выборочных исследований параметры 
и , a также пределы единиц выборки (площадь выборки) всегда известны. Опираясь на них, можно с точностью сказать, с каким доверием следует относиться к выборочным показателям.
(Фотометрический парадокс, парадокс Ольберса - это один из парадоксов космологии, заключающийся в том, что во Вселенной, равномерно заполненной звёздами, яркость неба (в том числе ночного) должна быть примерно равна яркости солнечного диска. Это должно иметь место потому, что по любому направлению неба луч зрения рано или поздно упрется в поверхность звезды.
Иными словами парадос Ольберса заключается в том, что если Вселенная бесконечна, то черного неба мы не увидим, так как излучение дальних звезд будет суммироваться с излучением ближних, и небо должно иметь среднюю температуру фотосфер звезд. При поглощении света межзвездным веществом, оно будет разогреваться до температуры звездных фотосфер и излучать также ярко, как звезды. Однако в дело вступает явление "усталости света", открытое Эдвином Хабблом, который показал, что чем дальше от нас расположена галактика, тем больше становится красным свет ее излучения, то есть фотоны как бы "устают", отдают свою энергию межзвездной среде. На очень больших расстояниях галактики видны только в радиодиапазоне, так как их свет вовсе потерял энергию идя через бескрайние просторы Вселенной. Подробнее читайте в FAQ по эфирной физике.
|
|
 |