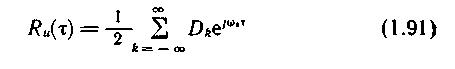
где
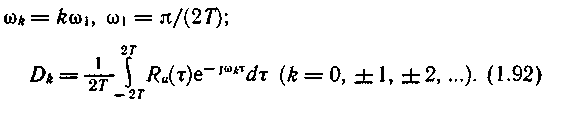
Учитывая, что
Ru(t ) является четной функцией, имеем
Положив ф = t1 - t2
, находим
что согласно (1.89) представляет собой каноническое разложение корреляционной функции. По нему, как было указано ранее, получаем каноническое разложение случайного процесса:
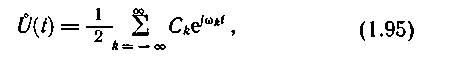
причем
Выражение (1.95) записано для случайного процесса с нулевой постоянной составляющей, что характерно для многих реальных сигналов. В общем случае в правую часть этого выражения необходимо добавить постоянную величину, соответствующую математическому ожиданию случайного процесса (
mu). Корреляционная функция при этом не изменяется.Очевидно, что при попарном объединении экспоненциальных составляющих с одинаковыми положительными и отрицательными индексами
k каноническое разложение (1.95) приводится к тригонометрической форме.Таким образом, стационарный случайный процесс на ограниченном интервале времени можно представить совокупностью гармонических составляющих различных частот с амплитудами, являющимися некоррелированными случайными величинами, математические ожидания которых равны нулю:
где
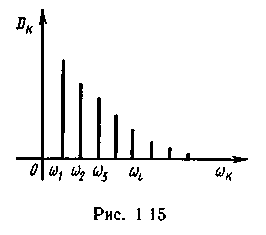
На спектральной диаграмме такого процесса каждой гармонике ставится в соответствие вертикальный отрезок, длина которого пропорциональна дисперсии ее амплитуды, а расположение на оси абсцисс отвечает частоте (рис.1.15).
Чтобы получить описание стационарного случайного процесса в точном смысле, т.е. справедливое для любого момента времени на бесконечном интервале -
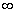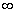<t<, необходимо перейти к интегральному каноническому разложению.
Непрерывные спектры. Интегральное каноническое разложение для корреляционной функции получим из формулы (1.91) путем предельного перехода при Т
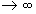. Увеличение интервала времени, на котором наблюдается случайный процесс, сопровождается уменьшением значений дисперсий, что следует из (1.92), а также сокращением расстояния между спектральными линиями, поскольку
При достаточно большом, но конечном Т можно записать выражение для средней плотности распределения дисперсии по частоте:
S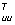
(w
k) = Dk / (
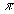(k = 0,±l, ±2,.) (1.98)
где
S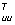(w
k) - средняя плотность дисперсии на участке, прилегающем к частоте щk.
Теперь можно преобразовать формулы (1.94) и (1.98) к виду
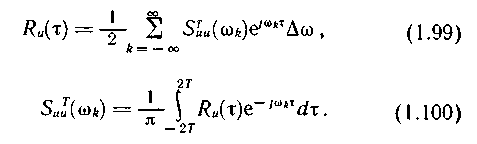
Переходя к пределу при Т
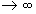, получаем
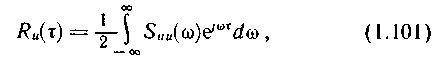
где
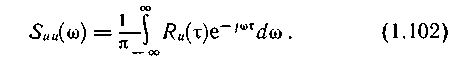
Так как величина
S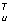
(щk) Дщ являлась не только дисперсией Dk коэффициента разложения корреляционной функции Ru(t
), но и дисперсией D [Ck] коэффициента разложения случайного процесса U(t), то величина Suu(w
) dw
, полученная в результате предельного перехода при Т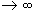
, представляет собой дисперсию, приходящуюся на спектральные составляющие стационарного случайного процесса, занимающие бесконечно малый интервал частот (щ, щ + dw
). Функцию Suu(w
), характеризующую распределение дисперсии случайного процесса по частотам, называют спектральной плотностью стационарного случайного процесса U(t).
Выражение для интегрального канонического разложения корреляционной функции
Ru(t ) найдем, положив в формуле (1.101) ф = t1 - t2: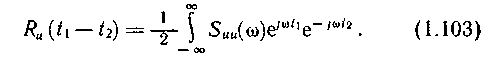
Обозначив
G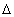
(w
) = Сk / (
w
) и повторив процедуру предельного перехода при T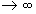 для соотношения (1.95), получим каноническое разложение стационарной случайной функции U(t):
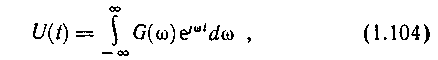
где дисперсией случайной функции
G(w ) dw является функция Suu(w ) dw .Поскольку понятие спектральной плотности стационарного случайного процесса играет большую роль при исследовании преобразования сигналов линейными системами, уточним ее свойства и физический смысл.
Основные свойства спектральной плотности. Отметим, что в формулах (1.101) и (1.102)
Suu(w ) определена как для положительных, так и для отрицательных частот. Перейдем к одностороннему спектру, ограничиваясь только положительными частотами. Воспользовавшись формулой Эйлера, представим соотношение (1.102) состоящим из двух слагаемых: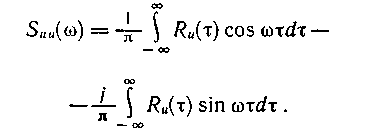
В силу четности функции
Ru(t ) второе слагаемое равно нулю, а первое можно преобразовать к виду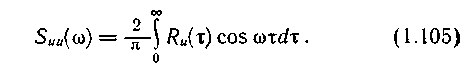
Из (1.105) следует, что
Suu(w ) является действительной и четной функцией, т.е.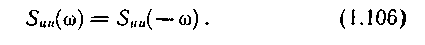
Это позволяет ограничиться положительными частотами и в (1.101):
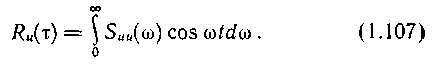
Соотношения (1 101) и (1.102), а также (1.105) и (1.107) являются парами интегрального преобразования Фурье, причем (1.105) и (1.107) для случая четной функции. Поэтому корреляционная функция и спектральная плотность подчинены закономерности: чем протяженнее кривая
Suu(щ), тем уже корреляционная функция Ru(t ) (тем меньше время корреляции), и наоборот.Площадь, ограниченная непрерывной кривой
Suu(w ) на спектральной диаграмме, очевидно, должна равняться дисперсии Du случайного процесса U(t). Действительно, положив в формуле (1.107) ф = 0, получим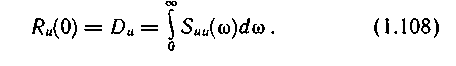
Подразумевая под случайным процессом
U(t) напряжение, Du можно рассматривать как среднюю мощность, выделяемую этим напряжением на резисторе с сопротивлением в 1 Ом:
Следовательно, величина
представляет собой долю средней мощности, выделяемой составляющими спектра, относящимися к интервалу частот (щ, щ
+ dw ).В связи с этим спектральную плотность
Suu(w ) называют еще спектральной плотностью мощности, а также энергетическим спектром стационарного случайного процесса, поскольку Suu(w ) имеет размерность энергии.Спектральная плотность мощности случайного процесса является средней характеристикой множества реализаций. Ее можно получить и путем усреднения спектральной мощности реализации Сk(щ) (1.62) по множеству реализаций.
Рассмотрим с этой целью одну реализацию
u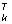
(t) стационарного случайного процесса U(t) сначала на ограниченном интервале времени - T<t<. T. Для нее можно записать преобразование Фурье:
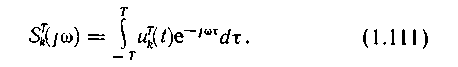
В соответствии с (1.63) спектральная плотность мощности этой реализации
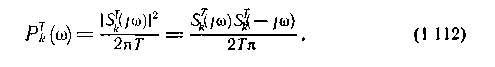
Найдем среднее значение С
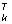(щ) по множеству реализации k. Имеем
или
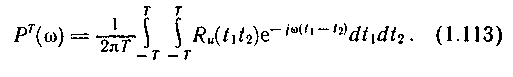
Так как мы предполагаем, что случайный процесс
U(t) стационарный, то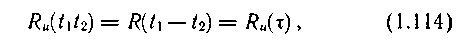
где
t1 - t2 = ф.При выполнении условия (1.114) для выражения (1.113) существует предел при
T: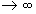
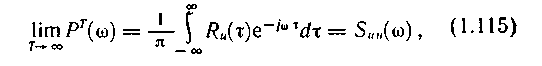
что и требовалось показать.
Пример 1.7 У центрированного стационарного случайного процесса спектральная плотность постоянна. Рассмотреть особенности такого процесса.
Пусть спектральная плотность
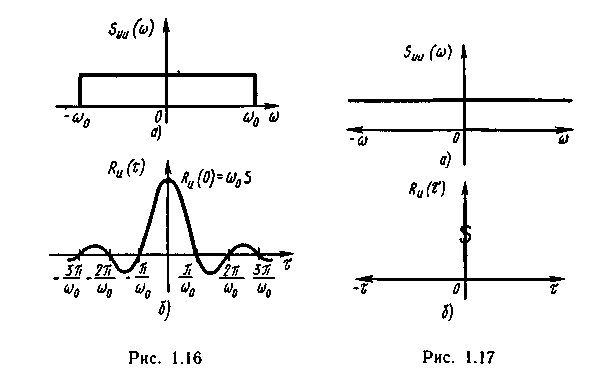
Suu(щ) ограничена определенной полосой частот (рис.1.16, а):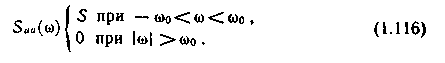
В соответствии с (1.107) найдем автокорреляционную функцию процесса
U(t):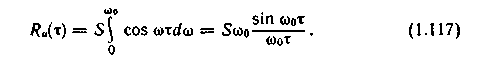
Вид функции
Ru(t ) приведен на рис.1.16,6. Значение ее при ф = 0 равно дисперсии, а следовательно, средней мощности рассматриваемого процесса:
Будем теперь расширять полосу частот, занимаемую энергетическим спектром (рис.1.17, а). Интервал времени, на котором наблюдается существенная корреляционная связь значений процесса, при этом уменьшается, а дисперсия
Du возрастает.При w
0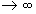 дисперсия становится безграничной, а корреляционная функция принимает вид дельта-функции (рис.1.17,6).
Идеализированный случайный процесс, энергетический спектр которого безграничен и равномерен, известен как "белый шум". Такое название возникло по аналогии с белым светом, имеющим равномерный и неограниченный спектр интенсивности. Основная особенность процесса в том, что его значения в любые два сколь угодно близкие моменты времени некоррелированы. Создать белый шум принципиально невозможно, так как реальные источники сигналов всегда имеют ограниченную мощность. Тем не менее, понятие "белый шум
" нашло широкое применение в информационной технике. Такая модель может быть принята, например, для сигналов (шумов), имеющих равномерный энергетический спектр в пределах полосы пропускания входного блока системы, в которой они рассматриваются.Иногда говорят о "реальном белом шуме", подразумевая стационарный случайный процесс с равномерным энергетическим спектром в пределах конечной, но достаточно широкой полосы частот.
Пример 1.8 Определить спектральную плотность мощности случайного процесса с линейно убывающей нормированной функцией автокорреляции (рис.1.18).
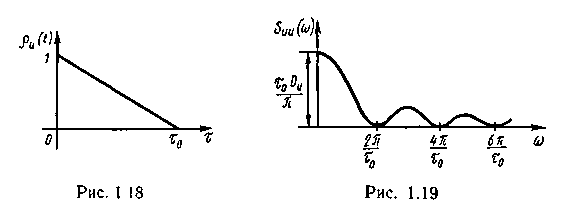
Аналитическое выражение нормированной корреляционной функции запишем в виде
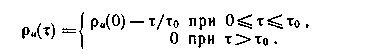
Воспользовавшись соотношением (1.105) при р„ (0) = 1, получим
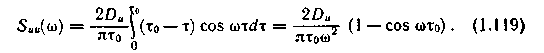
Раскрывая по правилу Лопиталя неопределенность выражения (1.119) при щ = 0, найдем
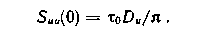
Несложный дополнительный анализ дает возможность определить форму кривой
Suu(w ) (рис.1. 19).Усталость света, анг. tired light - это явление потери энергии квантом электромагнитного излучения при прохождении космических расстояний, то же самое, что эффект красного смещения спектра далеких галактик, обнаруженный Эдвином Хабблом в 1926 г.
На самом деле кванты света, проходя миллиарды световых лет, отдают свою энергию эфиру, "пустому пространству", так как он является реальной физической средой - носителем электромагнитных колебаний с ненулевой вязкостью или трением, и, следовательно, колебания в этой среде должны затухать с расходом энергии на трение. Трение это чрезвычайно мало, а потому эффект "старения света" или "красное смещение Хаббла" обнаруживается лишь на межгалактических расстояниях.
Таким образом, свет далеких звезд не суммируется со светом ближних. Далекие звезды становятся красными, а совсем далекие уходят в радиодиапазон и перестают быть видимыми вообще. Это реально наблюдаемое явление астрономии глубокого космоса. Подробнее читайте в FAQ по эфирной физике.
|
|
 |