где
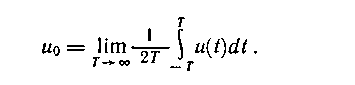
Обобщенную временную функцию
r(t ), не содержащую фазовой информации, назовем временной автокорреляционной функцией. Она показывает степень связи значений функции u(t), разделенных интервалом времени t , и может быть получена из статистической теории путем развития понятия коэффициента корреляции. Отметим, что во временной функции корреляции усреднение проводится по времени в пределах одной реализации достаточно большой продолжительности.Справедливо и второе интегральное соотношение для пары преобразования Фурье:
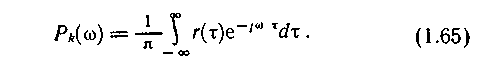
Пример 1.6 Определить временную функцию· автокорреляции гармонического сигнала
u(t) = u0 cos(w t-ц). В соответствии с (1.64)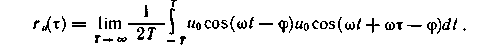
Проведя несложные преобразования
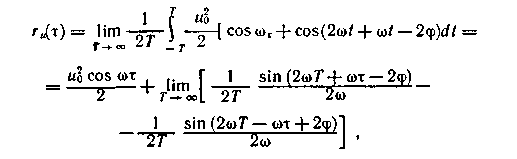
окончательно имеем
Как и следовало ожидать,
ru(t ) не зависит от ц и, следовательно, (1.66) справедливо для целого множества гармоник, различающихся фазами.Знаете ли Вы, низкочастотные электромагнитные волны частотой менее 100 КГц коренным образом отличаются от более высоких частот падением скорости электромагнитных волн пропорционально корню квадратному их частоты от 300 тыс. км/с при 100 кГц до примерно 7 тыс км/с при 50 Гц.
|
|
 |