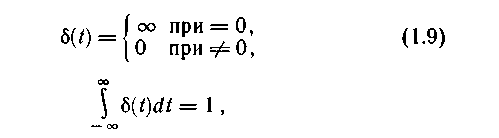
где д(t) - дельта-функция, отличная от нуля в начале координат (при
t = 0).Для более общего случая, когда дельта-функция отличается от нуля в момент времени
t=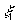
(рис.1.3), имеем
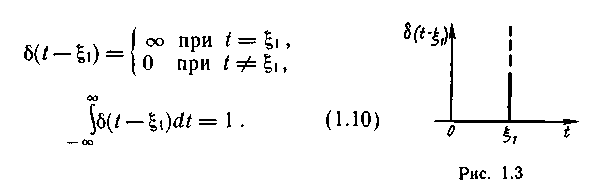
Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала
u(t) в конкретный момент времени ой: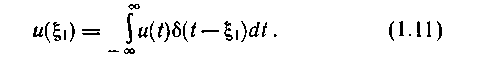
Равенство (1.11) справедливо для любого текущего момента времени
t. Заменив ой на t и приняв в качестве переменной интегрирования о, получим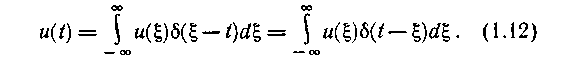
Таким образом, функция
u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с "площадями", равными соответствующим значениям входного сигнала.
С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через
u
(t) функцию, равную u(k
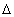t) в точках t = k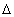t и нулю в остальных точках, запишем:
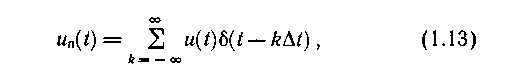
где Дt - период следования импульсов.
Поскольку умножение
u(t) на дельта - функцию в момент времени t = k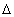t соответствует получению отсчета этой функции, uп(k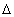t) может представлять результат равномерной дискретизации функции u(t).
Усталость света, анг. tired light - это явление потери энергии квантом электромагнитного излучения при прохождении космических расстояний, то же самое, что эффект красного смещения спектра далеких галактик, обнаруженный Эдвином Хабблом в 1926 г.
На самом деле кванты света, проходя миллиарды световых лет, отдают свою энергию эфиру, "пустому пространству", так как он является реальной физической средой - носителем электромагнитных колебаний с ненулевой вязкостью или трением, и, следовательно, колебания в этой среде должны затухать с расходом энергии на трение. Трение это чрезвычайно мало, а потому эффект "старения света" или "красное смещение Хаббла" обнаруживается лишь на межгалактических расстояниях.
Таким образом, свет далеких звезд не суммируется со светом ближних. Далекие звезды становятся красными, а совсем далекие уходят в радиодиапазон и перестают быть видимыми вообще. Это реально наблюдаемое явление астрономии глубокого космоса. Подробнее читайте в FAQ по эфирной физике.
|
|
 |