к библиотеке к оглавлению к дискретной математике технологии программирования

Факторный анализ

1. Общие понятия
2 Подготовка к факторному анализу
3 Нахождение первичной структуры факторов
- 3.1 Метод главных компонент
  - 3.1.1 Алгоритм NIPALS вычисления главных компонент
- 3.2 Другие методы
4 Вращение
- 4.1 Аналитическое вращение
  - 4.1.1 Ортогональное вращение
  - 4.1.2 Косоугольное вращение
    - 4.1.2.1 Методы введения вторичных осей
    - 4.1.2.2 Прямой метод облимин
Литература

Фрэнсис Гальтон - изобретатель факторного анализа

Истинное знание есть знание причин.
Френсис Бэкон

Общие понятия

Хозяйственные процессы и конечные результаты складываются под влиянием объективных и субъективных, внешних и внутренних факторов.

Фактор, factor - лат., делатель, творец чего-нибудь, то есть движущая сила, фактическая причина какого-нибудь процесса, обусловливающая его или определяющая его характер. В экономической информатике факторы - это причины, воздействующие на изучаемый экономический показатель. Одни из них непосредственно связаны между собой, другие - косвенно.

Например, на величину валовой продукции непосредственное влияние оказывают такие факторы, как численность рабочих и уровень производительности труда. Субъективные или косвенные факторы — внутренние (руководство тем или иным производственным коллективом, организация производства, финансов, экономическая или организационная подготовленность исполнителей и т.д.). Следовательно, это изучение и измерение влияния факторов на величину исследуемых экономических показателей. Без всестороннего и тщательного изучения факторов невозможно сделать обоснованные выводы о результатах деятельности, выявить резервы производства, обосновать планы и управленческие решения.

Факторный анализ - это методика комплексного и системного изучения и измерения воздействия факторов на величину результативного показателя. Факторы в результате анализа получают количественную и качественную оценку. Каждый показатель может в свою очередь выступать и в роли факторного, и результативного.

Например, в модели П = ВП - С (прибыль равна выручке за минусом себестоимости) прибыль - результативный показатель, а в модели R_пр = П / РП (рентабельность продаж равна прибыли, деленной на выручку от реализации) прибыль является фактором по отношению к результативному показателю рентабельности продаж.

Различают следующие противоположные типы факторного анализа:

детерминированный и стохастический;
прямой и обратный;
одноступенчатый и многоступенчатый;
статический и динамический;
ретроспективный (исторический) и перспективный (прогнозный).

Детерминированный факторный анализ - представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. когда результативный показатель представлен в виде произведения, частного или алгебраической суммы факторов. Взаимосвязи в детерминированном анализе можно формализовать и дать количественную оценку роли отдельных факторов на результативный показатель.

Стохастический факторный анализ - это методика исследования влияния факторов, связь которых с результатом является неполной. Носит характер вероятностной, корреляционной зависимости, поскольку изменение фактора может дать несколько значений результата в зависимости от сочетания других факторов. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, которые воздействуют на этот показатель.

Прямой факторный анализ - ведется дедуктивным способом - от общего к частному. Он проводится с целью комплексного исследования внутренних и внешних, объективных и субъективных факторов, формирующих величину изучаемого результативного показателя.

Обратный факторный анализ - осуществляет исследование причинно-следственных связей способом логической индукции - от частных, отдельных факторов к обобщающим, от причин к следствиям с целью установления чувствительности изменения многих результативных показателей к изменению изучаемого фактора.

Факторный анализ может быть одноуровневым и многоуровневым.

Одноуровневый факторный анализ - используется для исследования факторов только одного уровня (одной ступени) подчинения без их детализации на составные части. Например, y = ax+b.

Многоуровневый, многоступенчатый факторный анализ - проводит детализацию факторов а и b на составные элементы с целью изучения их сущности. Детализация факторов может быть продолжена. В таком случае изучается влияние факторов различных уровней соподчиненности.

Статический факторный анализ - применяется при изучении влияния факторов на результативные показатели на соответствующую дату.

Динамический факторный анализ - представляет собой методику исследования причинно-следственных связей в динамике.

Ретроспективный факторный анализ - изучает причины изменения результатов хозяйственной деятельности за прошлые периоды.

Перспективный факторный анализ - исследует поведение факторов и результативных показателей в перспективе.

Основные задачи факторного анализа:

Выявление, поиск факторов.
Отбор факторов для анализа исследуемых показателей.
Классификация и систематизация их с целью обеспечения системного подхода.
Моделирование взаимосвязей между результативными и факторными показателями.
Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя.
Работа с факторной моделью (практическое ее использование для управления экономическими процессами).

Факторный анализ - это один из способов снижения размерности, то есть выделения во всей совокупности признаков тех, которые действительно влияют на изменение зависимой переменной. Или группировки сходно влияющих на изменение зависимой переменной признаков. Или группировки просто сходно изменяющихся признаков. Предполагается, что наблюдаемые переменные являются лишь линейной комбинацией неких ненаблюдаемых факторов. Некоторые из этих факторов являются общими для нескольких переменных, некоторые характерно проявляют себя только в одной. Те, что проявляют себя только в одной, очевидно, ортогональны друг другу и не вносят вклад к ковариацию переменных, а общие - как раз и вносят эту ковариацию. Задачей факторного анализа является как раз восстановление исходной факторной структуры исходя из наблюдаемой структуры ковариации переменных, несмотря на случайные ошибки ковариации, неизбежно возникающие в процессе снятия наблюдения.

Коэффициент взаимосвязи между некоторой переменной и общим фактором, выражающий меру влияния фактора на признак, называется факторной нагрузкой (Factor load) данной переменной по данному общему фактору. Значение (мера проявления) фактора у отдельного объекта называется факторным весом объекта по данному фактору.

Процесс стохастического факторного анализа состоит из трех больших этапов:

Подготовки ковариационной матрицы (Иногда вместо нее используется корреляционная матрица);
Выделения первоначальных ортогональных векторов (основной этап);
Вращение с целью получения окончательного решения.

Подготовка к факторному анализу

При подготовке к факторному анализу часто (некоторые методы этого не требуют, но большая часть - требует) составляют ковариационные и корреляционные матрицы. Это матрицы, составленные из ковариации и корреляций векторов-атрибутов (строки и столбцы - атрибуты, пересечение - ковариация/корреляция).

Ковариация двух векторов:

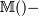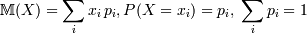
$\mathbb{M}() -$ математическое ожидание $\mathbb{M}(X)=\sum\limits_{i} x_i\, p_i , P(X=x_i) = p_i,\; \sum\limits_{i} p_i = 1$

Корреляция двух векторов:

$D[X] = M\left[(X -M[X])^2\right],$ - дисперсия.

Обратите внимание, что в этом случае корреляция и ковариация двух векторов - числа, так как считаются через матожидание вектора, а матожидание вектора - число.

Таким образом, мы переходим от матрицы, составленной из объектов (которые могут быть и не математическими), к матрице, оперирующей уже исключительно математическими понятиями, и абстрагируемся от объектов, уделяя внимания только атрибутам.

Нахождение первичной структуры факторов

Метод главных компонент

Метод главных компонент стремится выделить оси, вдоль которых количество информации максимально, и перейти к ним от исходной системы координат. При этом некоторое количество информации может теряться, но зато сокращается размерность.

Этот метод проходит практически через весь факторный анализ, и может меняться путем подачи на вход разных матриц, но суть его остается неизменной.

Основной математический метод получения главных осей - нахождение собственных чисел и собственных векторов ковариационной матрицы таких, что:

 $R V = λ V$ , где

$λ$ - собственное число R, R - матрица ковариации, V - собственный вектор R. Тогда :

 $R V - λ V = 0$ 
 $V (R - λ E) = 0$

и решение есть когда:

 $| R - λ E | = 0,$

где R - матрица ковариации, $λ$ - собственное число R, E - единичная матрица. Затем считаем этот определитель для матрицы соответствующей размерности.

V находим, подставляя собственные числа по очереди в

 $V (R - λ E) = 0$

и решая соответствующие системы уравнений.

Сумма собственных чисел равна числу переменных, произведение - детерминанту корелляционной матрицы. Собственное число представляет собой дисперсию оси, наибольшее - первой и далее по убыванию до наименьшего - количество информации вдоль последней оси. Доля дисперсии, приходящаяся на данную компоненту, считается отсюда легко: надо разделить собственное число на число переменных m.

Коэффициенты нагрузок для главных компонент получаются делением коэффициентов собственных векторов на квадратный корень соответствующих собственных чисел.

Алгоритм NIPALS вычисления главных компонент

На практике чаще всего для определения главных компонент используют итерационные методы, к примеру, NIPALS:

0. Задается $0 < ε 1 < 1$ - критерий окончания поиска главного компонента, и $0 < ε 2 < 1$ - критерий окончания поиска главных компонентов, исходная отцентрированная матрица $X$ , i=1 - номер главной компоненты.

1. Берется 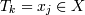$T_k = x_j \in X$ - вектор-столбец, k - шаг алгоритма, j - любой столбец (просто чтобы было с чего начинать апроксимизацию).

2. Вектор $T k$ транспонируется.

3. Считается 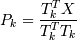$P_k = \frac {T_k^T X} {T_k^T T_k}$ .

4. $P k$ нормируется 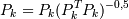$P_k=P_k (P_k^T P_k)^{-0,5}$

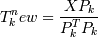
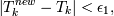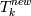5. Считается новый $T_k^new = \frac {X P_k} {P_k^T P_k}$

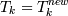6. Если $|T_k^{new} - T_k| < \epsilon_1 ,$ то $T_k^{new}$ и $P k$ - вектора весов и нагрузок соответственно для i-ой главной компоненты. Если нет, то $T_k=T_k^{new}$ и иди на 2.

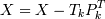7. $X=X-T_k P_k^T$ .

8. Если $| X | < ε$ , то стоп - найдены все основные компоненты, нас удовлетворяющие. Иначе i++. Иди на 1.

Другие методы

Метод сингулярных компонент

Метод максимального правдоподобия

Метод альфа-факторного анализа

Вращение

Вращение - это способ превращения факторов, полученных на предыдущем этапе, в более осмысленные. Бывает графическое (проведение осей, не применяется при более чем 2мерном анализе), аналитическое (выбирается некий критерий вращения, различают ортогональное и косоугольное) и матрично-приближенное (вращение состоит в приближении к некой заданной целевой матрице).

Результатом вращения является вторичная структура факторов. Первичная факторная структура (состоящая из первичных нагрузок (полученных на предыдущем этапе)) - это, фактически, проекции точек на ортогональные оси координат. Очевидно, что если проекции будут нулевыми, то структура будет проще. А проекции будут нулевыми, если точка лежит на какой-то оси. Де-факто вращение есть переход от одной системы координат к другой при известных координатах в одной системе(первичные факторы) и итеративно подбираемых координатах в другой системе (вторичных факторов).

При получении вторичной структуры стремятся перейти к такой системе координат, чтобы провести через точки (объекты) как можно больше осей, чтобы как можно больше проекции (и соответственно нагрузок) были нулевыми. При этом могут сниматься ограничения ортогональности и убывания значимости от первого к последнему факторам, характерные для первичной структуры, иВторичная структура является более простой, чем первичная, и потому более ценна.

Обозначим понятие простой структуры. Пусть r - число (общих) факторов первичной структуры , V - матрица вторичной структуры, состоящая из нагрузок (координат) вторичных факторов(строка - переменная из R, столбец - вторичный фактор).

В каждой строке матрицы V должен быть хотя бы 1 нулевой элемент;
Каждый столбец из матрицы V должен содержать не менее r нулей;
У одного из столбцов из любой пары из матрицы V должно быть несколько нулевых коэффициентов(нагрузок) в тех позициях, где для другого столбца они ненулевые (для различения);
При числе факторов больше 4 в каждой паре должно быть несколько нулевых нагрузок в одних и тех же строках;
Для каждой пары столбцов должно быть как можно меньше больших по величине нагрузок в одних и тех же строках.

Тогда структура будет хорошо подходить для интерпретации и будет выделяться однозначно. Наипростейшей является структура, где каждая переменная имеет факторную сложность(количество факторов, которые на нее влияют и оказывают факторную нагрузку), равную 1 (все факторы будут характерными). Реально это не достижимо, и потому мы стремимся приблизится к простой структуре при помощи различных методов. Существует эмпирическое правило, что для каждого фактора по крайней мере три переменных имеют значительную на него нагрузку.

Аналитическое вращение

Наиболее интересно аналитическое вращение, так как позволяет получить вторичную структуру исходя из достаточно критериев и без априорного знания о структуре факторной матрицы.

Ортогональное вращение

Ортогональное вращение подразумевает, что мы будем вращать факторы, но не будем нарушать их ортогональности друг другу. Ортогональное вращение подразумевает умножение исходной матрицы первичных нагрузок на ортогональную матрицу R(такую матрицу, что 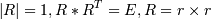$|R|=1, R*R^T=E, R= r \times r$ )

V=BR

Алгоритм ортагонального вращения в общем случае таков:

0. B - матрица первичных факторов.

1. Ищем ортогональную матрицу $R T$ размера 2*2 для двух столбцов(факторов) $b i$ и $b j$ матрицы B такую, что критерий для матрицы $[b i b j] R$ максимален.

2. Заменяем столбцы $b i$ и $b j$ на столбцы $[b_i b_j] \times R$ .

3. Проверяем, все ли столбцы перебрали. Если нет, то 1.

4. Проверяем, что критерий для всей матрицы вырос. Если да, то 1. Если нет, то конец.

Критерий квартимакс

Формализуем понятие факторной сложности q i-ой переменной через дисперсию квадратов факторных нагрузок факторов:

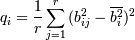$Формализация понятия факторной сложности$ ,

где r - число столбцов факторной матрицы, $b i j$ - факторная нагрузка j-го фактора на i-ю переменную, 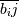$\overline {b_ij}$ - среднее значение. Критерий квартимакс старается максимизировать сложность всей совокупности переменных, чтобы достичь легкости интерпретации факторов (стремится облегчить описание столбцов):

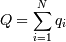
$Q=\sum_{i=1}^N{q_i}$

Учитывая, что 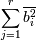$\sum_{j=1}^r{\overline {b_i^2}}$ - константа (сумма собственных чисел матрицы ковариации) и раскрыв среднее значение (а также учтя, что степенная функция растет пропорционально аргументу), мы получим:

Этот критерий и предполагается итеративно максимизировать. Этот критерий стремится к одному генеральному фактору.

Критерий варимакс

Этот критерий использует формализацию сложности фактора через дисперсию квадратов нагрузок переменной:

И тогда критерий в общем

При этом, как легко заметить, максимизируется сложность описания Факторные нагрузки могут нормироваться для избавления от влияния отдельных переменных. Дает лучшее разделение факторов, чем квартимакс.

Другие критерии

Можно обобщить два вышеприведенных критерия и получить новый:

 $M a x = α Q + β V$

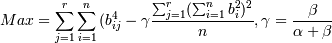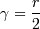Запишем его в следующем виде: $Max = \sum_{j=1}^r \sum_{i=1}^n {(b_{ij}^4} - \gamma \frac {\sum_{j=1}^r (\sum_{i=1}^n {b_i^2})^2}{n} , \gamma = \frac{\beta} {\alpha+\beta}$ Тогда при $γ = 0$ это квартимакс, при $γ = 1$ - варимакс, а при $\gamma = \frac {r}{2}$ - эвримакс, а при $γ = 0,5$ биквартимакс.

Косоугольное вращение

Косоугольное вращение не требует ортогональности между факторами. В остальном его алгоритм похож на ортогональное вращение. За счет этого можно получать больше нулей в факторных нагрузках и получать более характерные факторы. Правда, при этом возникает корреляция между факторами, что вообще не очень хорошо и приходится объяснять факторами 2го порядка. Их, кстати, тоже можно вычислить, причем используя ортогональное вращение и косоугольные факторы как исходные данные.

Методы введения вторичных осей

На основе квартимакса создается критерий квартимин:

где $a i j$ и $a i j$ - проекции на j-ю и k-ю оси. При применении ортогонального вращения этот критерий сводится к квартимаксу. При наипростейшей структуре N=0, а реально должно к нему стремится.

На основе варимакса создается критерий коваримин:

Минимизируется ковариация квадратов проекции на различные оси.

Объединение их, как и в ортогональном вращении, приводит к критерию облимин:

Прямой метод облимин

Используется критерий облимин, только при этом в качестве аргументов выступают нагрузки факторов первичной структуры:

d регулирует косоугольность решения, меньшие отрицательные d - больше ортогональность

к библиотеке к оглавлению к дискретной математике технологии программирования

Знаете ли Вы, почему "черные дыры" - фикция?
Согласно релятивистской мифологии, "чёрная дыра - это область в пространстве-времени, гравитационное притяжение которой настолько велико, что покинуть её не могут даже объекты, движущиеся со скоростью света (в том числе и кванты самого света). Граница этой области называется горизонтом событий, а её характерный размер - гравитационным радиусом. В простейшем случае сферически симметричной чёрной дыры он равен радиусу Шварцшильда".
На самом деле миф о черных дырах есть порождение мифа о фотоне - пушечном ядре. Этот миф родился еще в античные времена. Математическое развитие он получил в трудах Исаака Ньютона в виде корпускулярной теории света. Корпускуле света приписывалась масса. Из этого следовало, что при высоких ускорениях свободного падения возможен поворот траектории луча света вспять, по параболе, как это происходит с пушечным ядром в гравитационном поле Земли.
Отсюда родились сказки о "радиусе Шварцшильда", "черных дырах Хокинга" и прочих безудержных фантазиях пропагандистов релятивизма.
Впрочем, эти сказки несколько древнее. В 1795 году математик Пьер Симон Лаплас писал:
"Если бы диаметр светящейся звезды с той же плотностью, что и Земля, в 250 раз превосходил бы диаметр Солнца, то вследствие притяжения звезды ни один из испущенных ею лучей не смог бы дойти до нас; следовательно, не исключено, что самые большие из светящихся тел по этой причине являются невидимыми." [цитата по Брагинский В.Б., Полнарёв А. Г. Удивительная гравитация. - М., Наука, 1985]
Однако, как выяснилось в 20-м веке, фотон не обладает массой и не может взаимодействовать с гравитационным полем как весомое вещество. Фотон - это квантованная электромагнитная волна, то есть даже не объект, а процесс. А процессы не могут иметь веса, так как они не являются вещественными объектами. Это всего-лишь движение некоторой среды. (сравните с аналогами: движение воды, движение воздуха, колебания почвы). Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира