ТПОИ к оглавлению к дискретной математике технологии программирования

Методы и средства анализа данных

Поиск ассоциативных правил

4.1 Формальная постановка задачи
4.2 Представление результатов
4.3 Алгоритм Apriori
- 4.3.1 Свойство анти-монотонности
- 4.3.2 Описание алгоритма

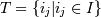Одной из наиболее распространённых задач анализа данных является определение часто встречающихся
наборов объектов в большом множестве наборов.
Впервые это задача была предложена поиска ассоциативных правил для нахождения типичных шаблонов покупок,
совершаемых в супермаркетах, поэтому иногда ее еще называют анализом рыночной корзины (market basket analysis).

Формальная постановка задачи

Пусть имеется база данных, состоящая из покупательских транзакций.
Каждая транзакция – это набор товаров, купленных покупателем за один визит. Такую транзакцию еще называют рыночной корзиной.

Пусть $I = {i i, i 2,..., i j,..., i n}$ – множество (набор) товаров (объектов) общим числом n.
Пусть D – множество транзакций $D = {T 1, T 2, T r,..., T m}$ , где каждая транзакция T – это набор элементов из I. 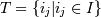$T=\{i_j|i_j \in I\}$ .

В сфере торговли, например, такими объектами являются товары, представленные в прайс-листе:

Идентификатор	Наименование товара	Цена
0	Шоколад	30
1	Хлеб	12
2	Масло	10
3	Вода	4
4	Молоко	14
5	Орехи	15

Они соответствуют следующему множеству объектов: I={шоколад, хлеб, масло, вода, молоко, орехи}.
Примерами транзакций могут быть $T 1$ = { хлеб, масло, молоко }, $T 2$ = { шоколад, вода, орехи }.
Множество транзакций, в которые входит объект $i j$ , обозначим следующим образом: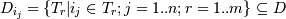
$D_{i_j} = \{T_r | i_j \in T_r; j=1..n; r=1..m\} \subseteq D$ .
Множество D может быть представлено следующим образом:

Номер транзакции	Номер товара	Наименование товара	Цена
0	1	Хлеб	12
0	3	Вода	4
0	4	Молоко	14
1	2	Масло	10
1	3	Вода	4
1	5	Орехи	15
2	5	Орехи	15
2	2	Масло	10
2	1	Хлеб	12
2	2	Масло	10
2	3	Вода	4
3	2	Масло	10
3	5	Орехи	15
3	2	Масло	10

В данном примере, множеством транзакций, содержащим объект "Вода", является следующее множество:

D(вода) = {{ хлеб, вода, молоко },
           { масло, вода, орехи },
{ орехи, масло, хлеб, масло, вода }}.

Некоторый произвольный набор объектов (itemset) обозначим следующим образом: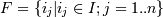
$F=\{i_j | i_j \in I; j = 1..n\}$ , например F = {хлеб, масло}.
Набор, состоящий из k элементов, называется k-элементным набором.
Множество транзакций, в которые входит набор F, обозначим следующим образом: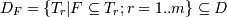
$D_F = \{T_r | F \subseteq T_r; r = 1..m\} \subseteq D$ .
В данном примере:

D(масло, вода) = {{ масло, вода, орехи },
{ орехи, масло, хлеб, масло, вода }}.

Отношение количества транзакций, в которое входит набор F, к общему количеству транзакций
называется поддержкой (support) набора F и обозначается Supp(F):
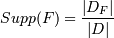$Supp(F) = \frac{|D_F|}{|D|}$ .
Для набора { масло, вода } поддержка будет равна 0,5, т.к. данный набор входит в две транзакции
с номерами 1 и 2, а всего транзакций четыре.
При поиске аналитик может указать минимальное значение поддержки интересующих его наборов $S u p p m i n$ .
Набор называется частым (large itemset), если значение его поддержки больше минимального значения поддержки,
заданного пользователем: $S u p p (F) > S u p p m i n$ .
Таким образом, при поиске ассоциативных правил требуется найти множество всех частых наборов:
$L = {F | S u p p (F) > S u p p m i n}$ .
В данном примере частыми наборами при $S u p p m i n = 0,5$ являются следующие:

{хлеб} $S u p p m i n = 0,5$ ;

{хлеб, вода} $S u p p m i n = 0,5$ ;

{масло} $S u p p m i n = 0,75$ ;

{масло, вода} $S u p p m i n = 0,5$ ;

{масло, вода, орехи} $S u p p m i n = 0,5$ ;

{масло, орехи} $S u p p m i n = 0,75$ ;

{вода} $S u p p m i n = 0,75$ ;

{вода, орехи} $S u p p m i n = 0,5$ ;

{орехи} $S u p p m i n = 0,75$ ;

Представление результатов

Решение задачи поиска ассоциативных правил, как и любой задачи, сводится к обработке
исходных данных и получению результатов. Результаты, получаемые при решении данной задачи
принято представлять в виде ассоциативных правил. В связи с этим в их поиске выделяю два этапа:

нахождение всех частых наборов объектов:
генерация ассоциативных правил из найденных частых наборов объектов.

Ассоциативные правила имеют следующий вид:

если (условие), то (результат),

где условие - обычно не логическое выражение (как в классификационных правилах),
а набор объектов из множества I, с которым связаны (ассоциированы) объекты, включенные
в результат данного правила.
Например, ассоциативное правило: "если (молоко, масло), то (хлеб)" означает, что если
потребитель покупает молоко и масло, то он покупает и хлеб.
Основным достоинством ассоциативных правил является их лёгкое восприятие человеком и
простая интерпретация языками программирования. Однако, они не всегда полезны.
Выделяют три вида правил:

полезные правила - содержат действительную информацию, которая ранее была неизвестна, но имеет логическое объяснение. Такие правила могут быть использованы для принятия решений, приносящих выгоду;
тривиальные правила - содержат действительную и легко объяснимую информацию, которая уже известна. Такие правила не могут принести пользу, т.к. отражают или известные законы в исследуемой области, или результаты прошлой деятельности. Иногда такие правила могут использоваться для проверки выполнения решений, принятых на основании предыдущего анализа;
непонятные правила - содержат информацию, которая не может быть объяснена. Такие правила могут быть получены на основе аномальных значений, или сугубо скрытых знаний. Напрямую такие правила нельзя использовать для принятия решений, т.к. их необъяснимость может привести к непредсказуемым результатам. Для лучшего понимания требуется дополнительный анализ.

Ассоциативные правила строятся на основе частых наборов. Так правила, построенные на основании набора F,
являются возможными комбинациями объектов, входящих в него.
Например, для набора {масло, вода, орехи}, могут быть построены следующие правила:

если (масло), то (вода); если (масло), то (орехи); если (масло), то (вода, орехи);
если (вода), то (масло); если (вода), то (орехи); если (вода), то (масло, орехи);
если (орехи), то (масло); если (орехи), то (вода); если (орехи), то (масло, вода);
если (масло, вода), то (орехи); если (масло, орехи), то (вода); если (вода, орехи), то (масло);

Таким образом, количество ассоциативных правил может быть очень большим и трудновоспринимаемым для человека.
К тому же, не все из построенных правил несут в себе полезную информацию.
Для оценки их полезности вводятся следующие величины:
Поддержка(support) - показывает, какой процент транзакций поддерживает данное правило.
Так как правило строится на основании набора, то, значит, правило X=>Y имеет поддержку, равную поддержке набора F,
который составл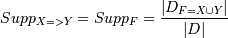яют X и Y:
$Supp_{X=>Y} = Supp_F = \frac{|D_{F=X \cup Y}|}{|D|}$ .
Очевидно, что правила, построенные на основании одного и того же набора, имеют одинаковую поддержку,
например, поддержка Supp(если (вода, масло), то (орехи) = Supp(вода, масло, орехи) = 0,5.

Достоверность(confidence) - показывает вероятность того, что из наличия в транзакции набора X следует наличие в ней набора Y.
Достоверностью правила X=>Y является отношение числа транзакций, содержащих X и Y, к числу транзакций, содержащих набор 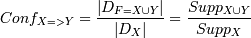Х:
$Conf_{X=>Y} = \frac{|D_{F=X \cup Y}|}{|D_X|} = \frac{Supp_{X \cup Y}}{Supp_X}$ .
Очевидно, что чем больше достоверность, тем правило лучше, причем у правил, построенных на основании одного и того же набора,
достоверность будет разная, например:

Conf(если (вода), то (орехи)) = 2/3;
Conf(если (орехи), то (вода)) = 2/3;
Conf(если (вода, масло), то (орехи)) = 1;
Conf(если (вода), то (орехи, масло)) = 2/3.

К сожалению, достоверность не позволяет определить полезность правила. Если процент наличия в транзакциях набора Y
при условии наличия в нем набора Х меньше, чем процент безусловного наличия набора Y, т.е.: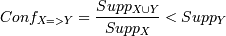
$Conf_{X=>Y} = \frac{Supp_{X \cup Y}}{Supp_X} < Supp_Y$ .
Это значит, что вероятность случайно угадать наличие в транзакции набора Y больше, чем предсказать это с помощью правила X=>Y.
Для исправления такой ситуации вводится мера - улучшение.
Улучшение(improvement) - показывает, полезнее ли правило случайного угадывания. Улучшение правила является отношением
числа транзакций, содержащих наборы X и Y, к произведению количества транзакций, содержащих набор Х, и количества транзакций,
содержащих набор Y: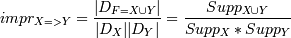
$impr_{X=>Y} = \frac{|D_{F=X \cup Y}|}{|D_X||D_Y|} = \frac{Supp_{X \cup Y}}{Supp_X * Supp_Y}$ .
Например, impr(если (вода, масло), то (орехи) = 0,5/(0,5*0,5) = 2.
Если улучшение больше единицы, то это значит, что с помощью правила предсказать наличие набора Y вероятнее, чем случайное угадывание,
если меньше единицы, то наоборот.
В последнем случае можно использовать отрицательное правило, т.е. правило, которое предсказывает отсутствие набор Y:
X => не Y.
Правда, на практике такие правила мало применимы. Например, правило: "если (вода, масло), то не (молоко)" мало полезно,
т.к. слабо выражает поведение покупателя.
Данные оценки используются при генерации правил. Аналитик при поиске ассоциативных правил
задает минимальные значения перечисленных величин. В результате те правила, которые не удовлетворяют этим условиям,
отбрасываются и не включаются в решение задачи. С этой точки зрения нельзя объединять разные правила, хотя и имеющие
общую смысловую нагрузку.
Например, следующие правила:

 $X = i 1, i 2 = > Y = i 3$ ,

 $X = i 1, i 2 = > Y = i 4$ ,

нельзя объединить в одно:

 $X = i 1, i 2 = > Y = i 3, i 4$ ,

т.к. достоверности их будут разные, следовательно, некоторые из них могут быть исключены, а некоторые - нет.

Алгоритм Apriori

Свойство анти-монотонности

Выявление часто встречающихся наборов элементов – операция, требующая много вычислительных ресурсов и, соответственно, времени.
Примитивный подход к решению данной задачи – простой перебор всех возможных наборов элементов.
Это потребует $O (2 | I |)$ операций, где |I| – количество элементов.
Apriori использует одно из свойств поддержки, гласящее: поддержка любого набора элементов не может превышать
минимальной поддержки любого из его подмножеств. Например, поддержка 3-элементного набора {Хлеб, Масло, Молоко}
будет всегда меньше или равна поддержке 2-элементных наборов {Хлеб, Масло}, {Хлеб, Молоко}, {Масло, Молоко}.
Дело в том, что любая транзакция, содержащая {Хлеб, Масло, Молоко}, также должна содержать {Хлеб, Масло}, {Хлеб, Молоко}, {Масло, Молоко},
причем обратное не верно.

Это свойство носит название анти-монотонности и служит для снижения размерности пространства поиска.
Не имей мы в наличии такого свойства, нахождение многоэлементных наборов было бы практически невыполнимой задачей
в связи с экспоненциальным ростом вычислений.

Свойству анти-монотонности можно дать и другую формулировку: с ростом размера набора элементов поддержка уменьшается,
либо остается такой же. Из всего вышесказанного следует, что любой k-элементный набор будет часто встречающимся тогда и только тогда,
когда все его (k-1)-элементные подмножества будут часто встречающимися.

Все возможные наборы элементов из I можно представить в виде решетки, начинающейся с пустого множества, затем
на 1 уровне 1-элементные наборы, на 2-м – 2-элементные и т.д. На k уровне представлены k-элементные наборы,
связанные со всеми своими (k-1)-элементными подмножествами.

Рассмотрим рисунок, иллюстрирующий набор элементов I – {A, B, C, D}.
Предположим, что набор из элементов {A, B} имеет поддержку ниже заданного порога и, соответственно, не является часто встречающимся.
Тогда, согласно свойству анти-монотонности, все его супермножества также не являются часто встречающимися и отбрасываются.
Вся эта ветвь, начиная с {A, B}, выделена фоном. Использование этой эвристики позволяет существенно сократить пространство поиска.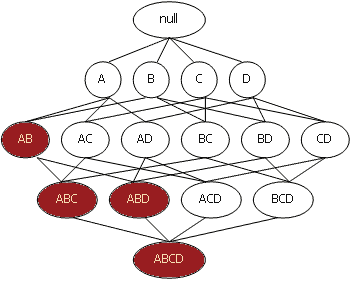

Описание алгоритма

Алгоритм Apriori определяет часто встречающиеся наборы за несколько этапов.
На i-ом этапе определяются все часто встречающиеся i-элементные наборы. Каждый этап состоит из двух шагов:

формирование кандидатов (candidate generation);
подсчет поддержки кандидатов (candidate counting).

Рассмотрим i-ый этап. На шаге формирования кандидатов алгоритм создает множество кандидатов из i-элементных наборов,
чья поддержка пока не вычисляется. На шаге подсчета кандидатов алгоритм сканирует множество транзакций,
вычисляя поддержку наборов-кандидатов. После сканирования отбрасываются кандидаты, поддержка которых меньше
определенного пользователем минимума, и сохраняются только часто встречающиеся i-элементные наборы.
Во время первого этапа выбранное множество наборов-кандидатов содержит все одно-элементные частые наборы.
Алгоритм вычисляет их поддержку во время шага подсчёта поддержки кандидатов.
Описанный алгоритм можно записать в виде следующего псевдокода:

  1. L1 = {часто встречающиеся 1-элементные наборы}
  2. для (k=2; Lk-1 <> ; k++) {
  3.   Ck = Apriorigen(Lk-1) // генерация кандидатов
  4.   для всех транзакций t T {
  5.     Ct = subset(Ck, t) // удаление избыточных правил
  6.     для всех кандидатов c Ct
  7.        c.count ++
  8.     }
  9.     Lk = { c 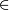 Ck | c.count >= minsupport} // отбор кандидатов
 10.   }
 11. Результат

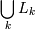
Обозначения, используемые в алгоритме:

Lk - множество k-элементных наборов, чья поддержка не меньше заданной пользователем. Каждый член множества имеет набор упорядоченных ( $i j < i p$ если j < p) элементов F и значение поддержки набора $S u p p F > S u p p m i n$ :

$L k = {(F 1, S u p p 1),(F 2, S u p p 2),...,(F q, S u p p q)}$ ,
где $F j = {i 1, i 2,..., i k}$ ;

Ck - множество кандидатов k-элементных наборов потенциально частых. Каждый член множества имеет набор упорядоченных ( $i j < i p$ если j < p) элементов F и значение поддержки набора Supp.

Опишем данный алгоритм по шагам.
Шаг 1. Присвоить k = 1 и выполнить отбор всех 1-элементных наборов, у которых поддержка больше минимально заданной пользователем $S u p p m i n$ .
Шаг 2. k = k + 1.
Шаг 3. Если не удается создавать k-элементные наборы, то завершить алгоритм, иначе выполнить следующий шаг.
Шаг 4. Создать множество k-элементных наборов кандидатов из частых наборов. Для этого необходимо объединить в k-элементные кандидаты (k-1)-элементные частые наборы. Каждый кандидат 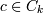$c \in C_k$ будет формироваться путём добавления к (k-1)-элементному частому набору - p элемента из другого (k-1)-элементного частого набора - q. Причем добавляется последний элемент набора q, который по порядку выше, чем последний элемент набора p $(p . i t e m k - 1 < q . i t e m k - 1)$ .
При этом все k-2 элемента обоих наборов одинаковы $(p . i t e m 1 = q . i t e m 1, p . i t e m 2 = q . i t e m 2,..., p . i t e m k - 2 = q . i t e m k - 2)$ .
Это может быть записано в виде SQL-подобного запроса:

insert into  $C k$ 
select  $p . i t e m 1, p . i t e m 2,..., p . i t e m k - 1, q . i t e m k - 1$ 
from  $L k - 1 p, L k - 1 q$ 
where  $p . i t e m 1 = q . i t e m 1, p . i t e m 2 = q . i t e m 2,..., p . i t e m k - 2 = q . i t e m k - 2, p . i t e m k - 1 < q . i t e m k - 1$

Шаг 5. Для каждой транзакции T из множества D выбрать кандидатов $C t$ из множества $C k$ , присутствующих в транзакции T. Для каждого набора из построенного множества $C k$ удалить набор, если хотя бы одно из его (k-1) подмножеств не является часто встречающимся т.е. отсутствует во множестве $L k - 1$ . Это можно записать в виде следующего псевдокода:

Для всех наборов  выполнить
  для всех (k-1)-поднаборов s из c выполнить
    если (), то
      удалить его из  $C k$

Шаг 6. Для каждого кандидата из $C k$ увеличить значение поддержки на единицу.
Шаг 7. Выбрать только кандидатов $L k$ из множества $C k$ , у которых значение поддержки больше заданной пользователем $S u p p m i n$ . Вернуться к шагу 2.
Результатом работы алгоритма является объединение всех множеств $L k$ для всех k.

ТПОИ к оглавлению к дискретной математике технологии программирования

Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира