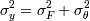
Методы, рассмотренные для правил и деревьев решений, работают наиболее естественно с категориальными переменными. Их можно адаптировать для работы с числовыми переменными, однако существуют методы, которые наиболее естественно работают с ними. Сегодня мы рассмотрим методы, которые используют математические функции в качестве правил для аналитики и прогнозирования.
Корреляционный анализ - это анализ переменных на предмет того, существует ли между ними какая-либо достаточно сильная зависимость. Нам требуется установить, влияют ли независимые переменные на зависимую - или это случайный набор данных. Следует отметить, тем не менее, что иногда даже корреляция не определяет причинности, а только то, что они изменяются по сходному закону. В общем, больше нам и не надо.
Очевидно, что, если мы решим использовать математические функции, то тогда зависимая переменная y будет вычисляться через какую-то функцию F (мы будем называеть ее функцией регрессии) от атрибутов X = < X1,...Xi,...Xn > . Однако очевидно также, что будет какая-то погрешность θ, (иначе все слишком хорошо, у нас просто прямая зависимость - впрочем, такое тоже возможно при θ = 0).
y = F(X) + θ
На интуитивном уровне можно сказать, что независимые переменные проецируются с некоторым разбросом (погрешностью) на плоскость Oy. (Рисунок). Тогда (опустив некоторые сложные математические выкладки) можно сказать, что:
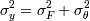
Это означает, что полная вариация зависимой переменной складывается из вариации функции регрессии F(X) () и вариации остаточной случайной компоненты.
В корреляционном анализе нас интересует, насколько изменчивость зависимой переменной обуславливается изменчивостью независимых переменных (функции от них). То есть:
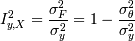
I - это индекс корреляции, 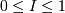 , основной показатель
корреляции переменных. В общем случае формулы для индекса корреляции нет, однако
иногда его можно оценить.
, основной показатель
корреляции переменных. В общем случае формулы для индекса корреляции нет, однако
иногда его можно оценить.
В том случае, если рассматривается двумерная нормальная (х и у распределены нормально) система (x,y), то тогда:
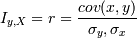
где r - коэффициент корреляции, еще один из достаточно сильных показателей взаимосвязи переменных. Положительный - они прямо пропорциональны, отрицательный - обратно. Однако для любого отклонения от двумерности и нормальности он не является прямо определяющим корреляцию.
В том случае, если есть отклонение от нормальности, то тогда имеет смысл попробовать разбить y на интервалы (сгруппировать по оси объясняющей переменной) и посчитать среди них среднее:
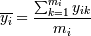 , где k - число
интервалов группировки, mi -
число точек в i-м интервале, yik - k-ая точка в i-м
интервале.
, где k - число
интервалов группировки, mi -
число точек в i-м интервале, yik - k-ая точка в i-м
интервале.
И тогда оценкой для 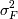 будет:
будет:
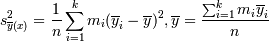
а для 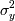 :
:
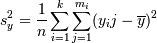
и тогда можно посчитать оценку для 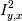 :
:
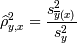
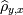 - корреляционное
отношение, оно похоже по свойствам на корреляционный коэффициент, но
несимметрично:
- корреляционное
отношение, оно похоже по свойствам на корреляционный коэффициент, но
несимметрично: 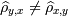 и не говорит о
характере связи.
и не говорит о
характере связи.
В том случае, если сгруппировать невозможно, то следует сначала провести регрессионный анализ и выявить коэффициенты функции регрессииw0,...wp, а затем считать
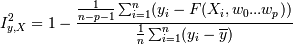
Для произdольного числа переменных Iy,x индекс корреляции называется коэффициентом корреляции Ry,X. Для линейного случая считается через попарные коэффициенты корреляции:
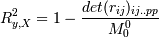 , где
, где 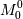 - минор
(определитель матрицы, получающейся из исходной матрицы rij вычеркиванием первого
(нулевого) столбца и строки)
- минор
(определитель матрицы, получающейся из исходной матрицы rij вычеркиванием первого
(нулевого) столбца и строки)
Этот коэффициент всегда больше любого коэффициента попарной корреляции.
Для нелинейного все опять же следует попробовать свести к интервалам, которые линеаризуются, или рассматривать регрессию.
Регрессионный анализ — метод моделирования измеряемых данных и исследования
их свойств. Данные состоят из пар значений зависимой переменной (переменной
отклика) и независимой переменной (объясняющей переменной). Регрессионная модель
есть функция независимой переменной и параметров с добавленной случайной
переменной. Параметры модели настраиваются таким образом, что модель наилучшим
образом приближает данные. Критерием качества приближения (целевой функцией)
обычно является среднеквадратичная ошибка: сумма квадратов разности значений
модели и зависимой переменной для всех значений независимой переменной в
качестве аргумента.
При построении математической функции классификации или
регрессии основная задача сводится к выбору наилучшей функции из всего множества
функций. Может существовать множество функций, одинаково классифицирующих одну и
ту же обучающую выборку.
В результате задачу построения функции классификации
и регрессии можно формально описать как задачу выбора функции с минимальной
степенью ошибки: 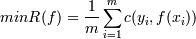
Где:
В случае бинарной классификации (принадлежности объекта к одному из двух
классов) простейшая функция потерь принимает значение 1 в случае неправильного
предсказания и 0 в противном случае.
Но здесь не учитывается ни тип ошибки,
ни её величина.
Для оценки качества классификации целесообразно использовать
разность f(x) - y. Разница между предсказанным и известным (по данным обучающей
выборки) значением зависимой переменной.
В случае когда регрессионная функция линейна, множество всех возможных
функций разбиения (F) можно представить в виде: 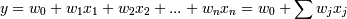 ,
,
где w0,w1,...,wn
- коэффициенты при независимых переменных.
Задача заключается в отыскании
таких коэффициентов w, чтобы разница между предсказанным и известным значением
зависимой переменной была минимальна. Также задачу можно сформулировать как
минимизация суммы квадратов разностей рассчитанных и известных значений
зависимой переменной. 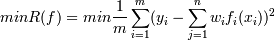
Нелинейные модели лучше классифицируют объекты, однако их построение более
сложно. Задача также сводится к минимизации выражения 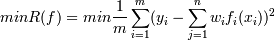 .
.
При этом
множество F содержит нелинейные функции.
В простейшем случае построение таких
функций сводится к построению линейных моделей. Для этого исходное пространство
объектов преобразуется к новому. В новом пространстве строится линейная функция,
которая в исходном пространстве является нелинейной. Для использования
построенной функции выполняется обратное преобразование в исходное пространство.
Если объекты их обучающей выборки отобразить графически (откладывая по одной оси
значение одной из независимых переменных, а по другой оси значение зависимой
переменной), то может получиться картина, когда объекты одного класса будут
сгруппированы в центре, а объекты другого рассеяны вокруг этого центра. В этом
случае применение линейных методов не поможет. Выходом из этой ситуации является
перевод объектов в другое пространство. Можно возвести координату каждой точки в
квадрат, тогда распределение может получиться таким, что станет возможным
применение линейных методов.
Описанный подход имеет один существенный
недостаток. Процесс преобразования достаточно сложен с точки зрения вычислений,
причём вычислительная сложность растёт с увеличением числа данных. Если учесть,
что преобразование выполняется два раза (прямое и обратное), то такая
зависимость не является линейной. В связи с этим построение нелинейных моделей с
таким подходом будет неэффективным. Альтернативой ему может служить метод
Support Vector Machines (SVM), не выполняющий отдельных преобразований всех
объектов, но учитывающий это в рассчётах.
Основная идея метода опорных векторов – перевод исходных векторов в пространство более высокой размерности и поиск максимальной разделяющей гиперплоскости в этом пространстве.
Каждый объект данных представлен, как вектор (точка в p-мерном пространстве (последовательность p чисел)). Рассмотрим случай бинарной классификации - когда каждая из этих точек принадлежит только одному их двух классов.
Нас интересует, можем ли мы разделить эти точки какой-либо прямой так, чтобы
с одной стороны были точки одного класса, а с другой - другого. Такая прямая
называется гиперплоскостью размерностью "p−1". Она описывается уравнением 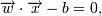 где
где 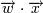 - скалярное
произведение векторов.
- скалярное
произведение векторов.
Тогда для того, чтобы разделить точки прямой, надо, чтобы выполнялось:
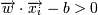 -> yi = 1 (принадлежит к одному
классу)
-> yi = 1 (принадлежит к одному
классу)
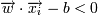 -> yi = − 1 (принадлежит к другому
классу)
-> yi = − 1 (принадлежит к другому
классу)
Для улучшения классификации попробуем найти такую разделяющую гиперплоскость, чтобы она максимально отстояла от точек каждого класса (фактически, разделим не прямой, а полосой).
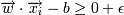 -> yi = 1 (принадлежит к одному
классу)
-> yi = 1 (принадлежит к одному
классу)
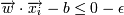 -> yi = − 1 для некоторого ε > 0
-> yi = − 1 для некоторого ε > 0
Домножим эти уравнения на константу так, чтобы для граничных точек - ближайших к гиперплоскости - выполнялось:
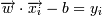
Это можно сделать, так как для оптимальной разделяющей гиперплоскости все граничные точки лежат на одинаковом от нее расстоянии. Разделим тогда неравенства на ε и выберем ε = 1. Тогда:
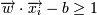 , если yi = 1
, если yi = 1 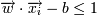 , если yi = − 1
, если yi = − 1
(Рисунок полосы)
Ширина разделительной полосы тогда равна 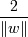 . Нам нужно, чтобы
ширина полосы была как можно большей (
. Нам нужно, чтобы
ширина полосы была как можно большей ( 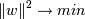 )(чтобы классификация
была точнее) и при этом
)(чтобы классификация
была точнее) и при этом 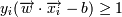 (так как
(так как 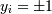 ). Это задача
квадратичной оптимизации.
). Это задача
квадратичной оптимизации.
Это в том случае, если классы линейно разделимы (разделимы гиперплоскостью). В том случае, если есть точки, которые лежат по "неправильные" стороны гиперплоскости, то мы считаем эти точки ошибками. Но их надо учитывать:
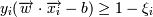 , ξi - ошибка xi, если ξi = 0 - ошибки нет, если 0 < ξi < 1, то объект внутри
разделительной полосы, но классифицируется правильно, если ξi > 1 - это ошибка.
, ξi - ошибка xi, если ξi = 0 - ошибки нет, если 0 < ξi < 1, то объект внутри
разделительной полосы, но классифицируется правильно, если ξi > 1 - это ошибка.
Тогда нам надо минимизировать сумму 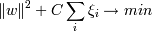 , C - параметр,
позволяющий регулировать, что нам важнее - отсутствие ошибок или выразительность
результата (ширина разделительной полосы), мы его выбираем сами .
, C - параметр,
позволяющий регулировать, что нам важнее - отсутствие ошибок или выразительность
результата (ширина разделительной полосы), мы его выбираем сами .
Как известно, чтобы найти минимум, надо исследовать производную. Однако у нас заданы еще и границы, в которых этот минимум искать! Это решается при помощи метода Лагранжа: Лагранж доказал (для уравнений в общем и неравенств в частности), что в той точке, где у функции F(x) условный (ограниченный условиями) минимум, в той же точке у функции
| F(x) − | ∑ | λiGi |
| i |
(для фиксированного набора λi,Gi - условия
ограничений) тоже минимум, но уже безусловный, по всем x. При этом либо λi = 0 и соответственно ограничение Gi не активно, либо 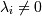 , тогда неравенство
Gi превращается в уравнение.
, тогда неравенство
Gi превращается в уравнение.
Тогда алгоритм поиска минимума следующий:
| F(x) − | ∑ | λiGi |
| i |
по х и приравнять их к нулю.
Тогда можно нашу задачу ( минимизировать 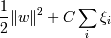 при условиях
при условиях 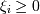 ,
, 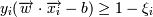 ) сформулировать при
помощи метода лагранжа следующим образом:
) сформулировать при
помощи метода лагранжа следующим образом:
Необходимо найти минимум по w, b и ξi и максимум по λi функции 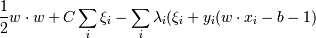 при условиях
при условиях 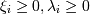 .
.
Возьмем производную лагранжианы по w, приравняем ее к нулю и из полученного выражения выразим w:
| w = | ∑ | λiyixi |
| i |
Следовательно, вектор w - линейная комбинация учебных векторов xi, причем только таких, для
которых 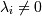 . Именно эти вектора
называются опорными и дали название метода.
. Именно эти вектора
называются опорными и дали название метода.
Взяв производную по b, получим
| ∑ | λiyi = 0 |
| i |
.
Подставим w в лагранжиану и получим новую (двойственную) задачу:
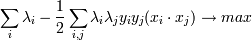 при
при
| ∑ | λiyi = 0 |
| i |
, 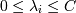
Это финальная задача, которую нам надо решить. Обратите внимание, что в итоге все свелось к скалярному произведению двух векторов - xi и xj. Это произведение называется Ядром.
Эта задача решается методом последовательных оптимизации (благодаря тому, что коэффициенты при λiλj положительны -> функция выпуклая -> локальный максимум яявляется глобальным):
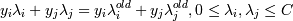 находим пару таких
λi,λj, при
которых
находим пару таких
λi,λj, при
которых 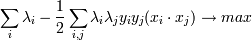 (мини-оптимизация);
(мини-оптимизация);
Это все хорошо, если набор хотя бы более-менее линеен (когда ошибка достаточно мала). В том случае, если набор не линеен, тогда ошибка велика. В 1992 году Бернхард Босер, Изабель Гуйон и Вапник предложили способ создания нелинейного классификатора, в основе которого лежит переход от скалярных произведений к произвольным ядрам, так называемый kernel trick , позволяющий строить нелинейные разделители.
Результирующий алгоритм крайне похож на алгоритм линейной классификации, с той лишь разницей, что каждое скалярное произведение в приведенных выше формулах заменяется нелинейной функцией ядра (скалярным произведением в пространстве с большей размерностью). В этом пространстве уже может существовать оптимальная разделяющая гиперплоскость. Так как размерность получаемого пространства может быть больше размерности исходного, то преобразование, сопоставляющее скалярные произведения, будет нелинейным, а значит функция, соответсвующая в исходном пространстве оптимальной разделяющей гиперплоскости будет также нелинейной.
Стоит отметить, что если исходное пространство имеет достаточно высокую размерность, то можно надеяться, что в нём выборка окажется линейно разделимой.
Наиболее распространенные ядра:
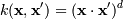
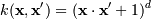
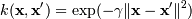 , для γ > 0
, для γ > 0
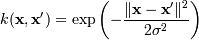
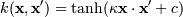 , для почти всех
κ > 0 и c <
0
, для почти всех
κ > 0 и c <
0 |
|