Переходные процессы при L=0 и “медленных” изменениях воздействующего фактора

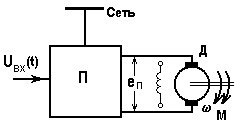
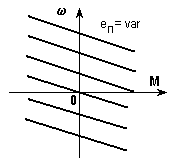
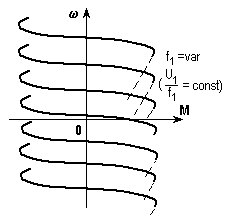
К задачам данной группы ранее были отнесены переходные процессы в системе преобразователь - двигатель (П-Д). Фактор, вызывающий переходный процесс, изменяется не мгновенно (темп его изменения соизмерим с темпом изменения скорости привода в переходном процессе); учитывается только механическая инерция в приводе (J), индуктивности в цепях двигателя малы или не проявляются.

Типичные структуры системы П-Д и соответствующие механические характеристики показаны на рис. 11 и 12.

а) б)

Рис. 11. Система ПН-ДПТ и ее механические характеристики

Роль преобразователя П в схеме на рис. 11, как отмечалось, может играть генератор (система Г-Д) или тиристорный преобразователь (ТП-Д). Фактор, вызывающий переходный процесс в этих системах, - изменение входного сигнала u_вх, приводящее к изменению ЭДС преобразователя е_п.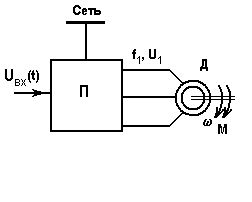

а) б)

Рис. 12. Система ПЧ-АД и ее механические характеристики

Роль преобразователя П в схеме на рис. 12 играет статический преобразователь частоты. Фактор, вызывающий переходный процесс в этих системах, - изменение входного сигнала u_вх, приводящее к изменению частоты и напряжения на выходе преобразователя.

Как и прежде, целью изучения переходных процессов в системе П-Д будет определение зависимостей w (t), М(t) и иногда i(t) при известных условиях переходного процесса и параметрах привода.

Введем ряд условий и допущений.

1. Механические характеристики привода w (М) известны, линейны (по крайней мере, на рабочих участках) и параллельны друг другу, то есть выражаются уравнением (4):

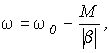
где 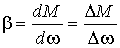- жесткость характеристик.

2. Известны или могут быть определены зависимости е_п(t) или f₁(t), то есть закон изменения во времени фактора, вызывающего переходный процесс. Так как е_п или f₁однозначно связаны со скоростью идеального холостого хода привода w ₀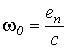

- для схемы на рис. 11,

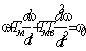- для схемы на рис. 12,

то известен закон изменения во времени w ₀.

3. Известно начальное (w _нач, М_нач) и конечное (w _кон, М_кон) состояние привода, момент инерции J и момент сопротивления М_с = const.

4. Преобразователь П обладает двусторонней проводимостью, то есть характеристики w (М) могут располагаться во всех квадрантах плоскости w , М.

Рассмотрим прежде всего качественные отличия переходных процессов в системе П-Д от изученных ранее случаев, когда е_п или f₁изменялись мгновенно, то есть мгновенно устанавливалась соответствующая новая механическая характеристика, а изменение скорости w и момента М в переходном процессе происходило согласно именно этой характеристике. Переходный процесс определялся статической механической характеристикой привода.

В рассматриваемых далее задачах е_п или f₁изменяются, как указывалось, не мгновенно, то есть переход привода с одной характеристики на другую происходит постепенно, одновременно с изменением скорости, в результате чего соответствие между скоростью w и моментом М в каждый момент времени определяется не статической механической характеристикой, а другой, отличной от нее характеристикой, которую мы далее будем называть динамической механической характеристикой или просто динамической характеристикой.

В качестве примера на рис. 13 показана статическая характеристика асинхронного двигателя при номинальной частоте 1, по которой будет происходить пуск при мгновенном приложении к двигателю напряжения такой частоты, и динамическая характеристика 2, соответствующая пуску двигателя путем плавного изменения частоты от нуля до номинальной по некоторому закону.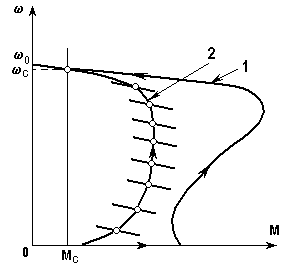

Рис. 13. Статическая 1 и динамическая 2 механические характеристики

Динамические характеристики определяются темпом изменения фактора, вызывающего переходный процесс, и параметрами привода, могут очень сильно отличаться от статических характеристик и даже иметь совсем другую форму.

Легко обнаружить связь зависимостей w (t) и М(t) с динамической характеристикой привода: исключив время t из уравнений w (t) и М(t), мы получим динамическую характеристику.

а) Уравнения, описывающие переходные процессы.

Из уравнения механической характеристики (4) получим:

М = Ѕ b Ѕ w _{0 -}Ѕ b Ѕ w . (5,а)

Подставив (5,а) в уравнение движения (1), после элементарных преобразований будем иметь:

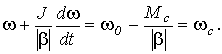(13)

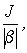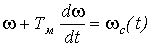Коэффициент при производной как и раньше, - электромеханическая постоянная времени Т_м. Правая часть уравнения представляет собою скорость w _с, соответствующую моменту сопротивления М_с, однако, в рассматриваемом случае w ₀ , а значит и w _с не постоянные величины, а известные функции времени w ₀(t) и w _c(t). Таким образом, уравнение (13) имеет вид:

. (14)

Решение этого дифференциального уравнения определит искомую зависимость w (t).

Для получения зависимости М(t) удобно воспользоваться непосредственно уравнением движения (1), подставив в него производную найденной функции w (t):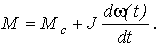

(15)

Правая часть уравнения (14), вообще говоря, может иметь любой вид. Закон w ₀(t) в случае безынерционного преобразователя формируется на его входе; при инерционном преобразователе закон w ₀(t) связан со свойствами преобразователя. В ряде случаев закон w ₀(t) формируется таким образом, чтобы получить требуемый закон w (t).

б) Уравнение переходных процессов при линейном законе w _с(t)

Получим решение уравнения (14) для одного важного вида функции w _с(t) - для линейного изменения w _с во времени:

w _с(t) = а + kt. (16)

Такой закон может быть сформирован при безынерционном преобразователе с помощью задатчика интенсивности.

Мы используем здесь общее уравнение прямой, не накладывая пока никаких ограничений на величины а и k с тем, чтобы, рассматривая частные случаи, можно было пользоваться полученным общим результатом.

Уравнение (14) с учетом (16) имеем вид:

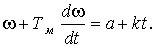(17)

Решение будем искать, как и прежде, в виде суммы свободной w _св и принужденной w _прсоставляющих:

w = w _св + w _пр . (*)

Свободная составляющая, то есть решение однородного уравнения, полученного из (17) имеет вид:

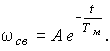
Принужденную составляющую будем искать, учитывая (16), в виде:

w _пр = В + kt,

так как в установившемся режиме скорость будет линейно изменяться во времени. Подставив w _пр в (17) получим:

В + kt + kT_м = a + kt

или

B = a - kT_м.

Подставим теперь w _св иw _пр в (*):

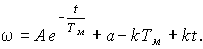
Постоянную А найдем, используя начальные условия: при t = 0 w = w _нач:

w _нач = А + а - kT_м,

откуда

А = w _нач - а + kT_м

Окончательно будем иметь:

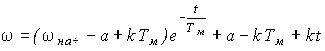. (18)

Перейдем теперь к рассмотрению некоторых конкретных переходных процессов в системе П-Д.

в) Пуск вхолостую.

Будем полагать, что закон изменения во времени фактора, вызывающего переходный процесс, е_п или f₁ или в общем случае w ₀ имеет вид, представленный на рис. 14 справа вверху. Так как М_с = 0 (пуск вхолостую), то w _с = (t) будет совпадать с w ₀(t) - см. уравнение (13), т.е. а = 0 и

где e - ускорение, характеризующее темп изменения w ₀;

при 0 < t < t₁ w _с(t) = e t;

при t > t₁ w _с(t) =w ₀₁ = сonst.

Излом функции w _с(t) при t = t₁ свидетельствует о том что переходный процесс состоит из двух этапов, и его необходимо рассчитать отдельно для каждого участка.

I этап (0 < t < t₁).

Приняв, что при t = 0 w _нач= 0 и подставив в (18) а = 0, k = e , получим

(19)

Рис. 14. Механические характеристики и графики переходного процесса при пуске вхолостую с w ₀(t) = e t

Воспользовавшись уравнением (15), найдем закон изменения момента во времени:

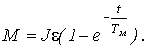(20)

Проанализируем полученные уравнения.

Ускорение привода определится как

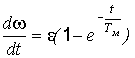
и при t = 0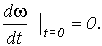 Этот результат очевиден: при t = 0 w _с = w ₀= 0 т.е. е_п = 0 или f₁ = 0, привод не развивает момента и в соответствии с уравнением движения (1) 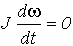и .

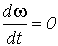При t > 3Т_м 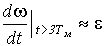, т.е. скорость изменяется в том же темпе, что и фактор, вызывающий переходный процесс. Из уравнения (19) следует, что при t > 3Т_м

w = e (t - Т_м) = w _с(t) - e Т_м. (19,а)

Графики w _с(t) и w (t) представлены на рис. 14. Кривая w (t) сдвинута вправо относительно кривой w _с(t) на величину Т_м; в каждый момент времени при t > 3Т_м разница между w _с и w составляет e Т_м.

Момент в соответствии с (20) возрастает по экспоненциальному закону (см. рис. 14) и при t > 3Т_м достигает величины

M_макс = Je . (20,а)

Это соотношение позволяет оценить допустимую величину e . Действительно, если считать, что в переходном процессе М_макс = М_доп, то

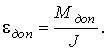
В частности, можно найти минимальное время пуска привода при котором момент не превысит допустимого значения:

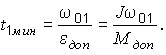
Если положить, что М_доп = 2 М_н, а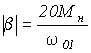 , что справедливо для нормальной электрической машины средней мощности, то получим

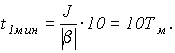
II этап (t > t₁).

На II этапе w _с =w ₀₁ , а значит, и е_пили f₁ имеют постоянную величину. Переходный процесс в этом случае ничем не отличается от рассмотренных ранее переходных процессов, отнесенных к первой группе задач. Если отсчитывать время от t₁, (точка 0’), то скорость w и момент М будут изменяться в соответствии с уравнением (10); в качестве х_нач следует принять значения w и М в момент времени t₁. Если t₁< 3Т_м, начальные значения должны быть лпределены по (19) и (20) при подстановке в эти уравнения t = t₁.

В качестве х_кон, очевидно, следует взять w ₀₁ и 0.

Графики w (t) и M(t) на II этапе показаны на рис. 14. Там же слева приведена динамическая механическая характеристка для случая пуска вхолостую.

Все рассмотренные выше величины и зависимости имеют очевидный физический смысл для системы П-Д с двигателем постоянного тока. Действительно,

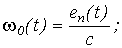
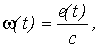
т.е. кривая w ₀(t) представляет собою в некотором масштабе закон изменения во времени е_п, а кривая w (t) - закон изменения е в том же масштабе. Разность этих величин в соответствии с вторым законом Кирхгофа определит ток, протекающий в якорной цепи: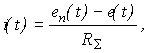

а значит, и момент, развиваемый двигателем

M(t) = ci(t).

г) Реверс (торможение) вхолостую.

Для осуществления реверса w ₀должна изменить направление. Это значит, что е_п уменьшается до 0, затем изменяет полярность и возрастает до заданной величины, либо f₁ уменьшается до 0, меняется чередование фаз и f₁ возрастает до заданной величины.

Как и прежде, будем считать, что изменение w ₀ во времени осуществляется по линейному закону при (0 < t < t₁), затем при t > t_{1 w 0}= w ₀₁. Таким образом, переходный процесс состоит из двух участков, которые следует рассматривать отдельно. Так как переходный процесс осуществляется вхолостую (М_с = 0), то w _с(t) = w ₀(t).

I этап (0 < t < t₁).

На I этапе изменение w _с(t) можно представить уравнением (16), подставив в него а = w ₀₁, k = -e . Тогда, воспользовавшись уравнением (18), в котором w _нач= w ₀₁, получим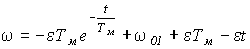

или

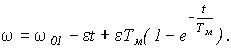(21)

Уравнение (16) определяет закон изменения М во времени:

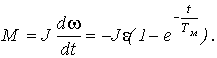(22)

Проанализируем полученные уравнения.

Ускорение привода

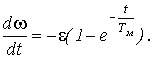
При t = 0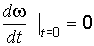 , что очевидно и с физической точки зрения: при t = 0 М= 0 т.е. 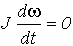и .

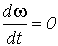При t > 3Т_м 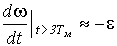, т.е. как и при пуске, скорость изменяется в том же темпе, что и фактор, вызвавший переходный процесс. При t > 3Т_м

w = w ₀₁ - e (t - Т_м) = w _с(t) + e Т_м,

т.е. как и при пуске, кривая w (t) располагается правее кривой w _с(t) , причем сдвиг по оси t составляет величину Т_м, а в каждый момент времени при t > 3Т_м разница между w _с и w составляет e Т_м.

Момент отрицателен и изменяется по экспоненциальному закону до величины

M_макс = - Je .

II этап (t > t₁).

Переходные процессы на II этапе подчиняются уравнению (10) и рассчитывается очевидным образом.

Кривые w _с(t), w (t) и М(t) и динамическая характеристика показаны на рис. 15.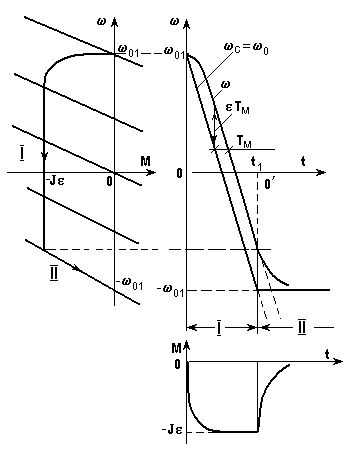

Рис. 15. Механические характеристики и графики переходного

процесса при реверсе вхолостую с w ₀(t) = -e t

При торможении вхолостую w ₀ изменяется от значения w ₀₁ до нуля. Как и при реверсе, процесс состоит из двух этапов, причем на I этапе (0 < t < t₁ ) кривые w (t) и М(t) не отличаются от аналогичных кривых при реверсе, а на II этапе - подчиняются уравнению (10) с соответствующими х_нач и х_кон.

Кривые w (t) и М(t), а также динамическая характеристика показана на рис. 16.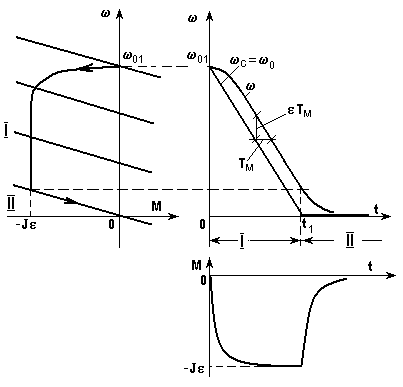

Рис. 16. Механические характеристики и графики переходного

процесса при торможении вхолостую с w ₀(t) = -e t

Рассмотрим кратко порядок операций при построении кривых переходного процесса в рассматриваемых случаях.

1. Изображается w _с(t), в рассмотренных случаях w _с(t)= w ₀(t); отмечаются этапы и определяется e на этапе, где w _с(t) изменяется.

2. Проводится линия, параллельная w _с(t) и сдвинутая вправо на Т_м, - это и будет основа графика w (t).

3. Корректируется график w (t) на начальном и конечном (II) участках, введением экспонент с постоянной времени Т_м.

4. Строится основа графика М(t) - прямоугольник со сторонами 0 - t₁ и Je ; в случае реверса и торможения e имеет отрицательный знак.

5. Корректируется график М(t) на начальном и конечном участках, введением экспонент с постоянной времени Т_м.

Переходные процессы под нагрузкой.

Общие формулы (15) и (18) справедливы и для этого случая, вместе с тем различия в характере нагрузки - М_с может быть как активным, так и реактивным - и в начальных условиях делают задачи разнообразными и иногда не очень простыми.

Выясним прежде всего, как будет изменяться правая часть (13), т.е. w _с(t) =w ₀(t) - М_с / к b Ѕ , при тех же, что и прежде, изменениях w ₀(t), но различном характере М_с.

Как показано на рис. 17, при активном моменте сопротивления w _с(t) располагается ниже w ₀(t) на D w и никаких существенных отличий в алгоритме решения задачи нет. Единственное, пожалуй, о чем следует позаботиться, - о правильном учете начальных условий при пуске. Возможны два случая - первый, когда при t = 0 w = 0, т.е. когда растормаживание привода с активным моментом и начало роста w ₀(t) совпадают, и второй, когда до начала пуска привод вращался под действием активного М_с с небольшой скоростью -D w - пунктир на рис. 17.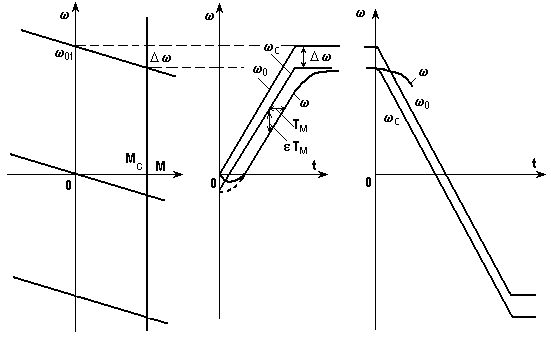

Рис. 17. Переходный процесс пуска при активном М_с

При пуске с реактивным М_с(рис. 18) скорость начинает изменяться через некоторое время t_з, за которое момент двигателя вырастет до значения М_с. В качестве примера на рис. 18 показаны все кривые, соответствующие этому случаю.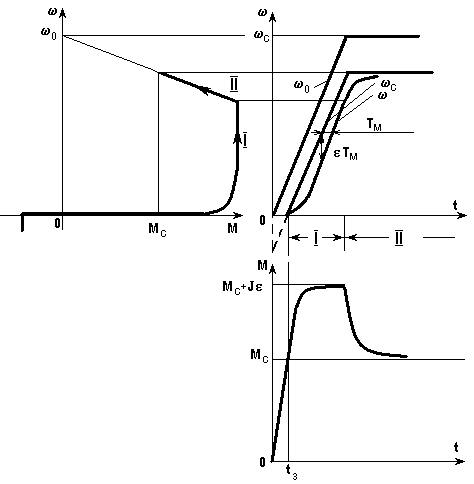

Рис. 18. Переходный процесс пуска при реактивном М_с

При реверсе с реактивным М_с имеются две ветви w _с(t), причем переход с одной на другую осуществляется в момент времени, когда скорость, достигнув нулевого значения, изменит знак.

Таким образом, как следует из изложенного в системе преобразователь - двигатель можно формировать любые требуемые динамические характеристики.

к оглавлению

Знаете ли Вы, что "тёмная материя" - такая же фикция, как черная кошка в темной комнате. Это не физическая реальность, но фокус, подмена.
Реально идет речь о том, что релятивистские формулы не соответствуют астрономическим наблюдениям, давая на порядок и более меньшую массу и меньшую энергию. Отсюда сделан фокуснический вывод, что есть "темная материя" и "темная энергия", но не вывод, что релятивистские формулы не соответствуют реалиям. Подробнее читайте в FAQ по эфирной физике.

НОВОСТИ ФОРУМА

Рыцари теории эфира