EWB. Устройство контроля четности

Операция контроля четности двоичных чисел позволяет повысить надежность передачи и обработки информации. Ее сущность заключается в суммировании по модулю 2 всех разрядов с целью выяснения четности числа, что позволяет выявить наиболее вероятную ошибку в одном из разрядов двоичной последовательности. Например, если при передаче кода 1001 произойдет сбой во втором разряде, то на приемном пункте получим код 1101 — такую ошибку определить в общем случае затруднительно. Если же код относится к двоично-десятичному (8-4-2-1), то ошибку легко обнаружить, поскольку полученный код (десятичный эквивалент — число 13) не может в принципе принадлежать к двоично-десятичному.

Обнаружение ошибок путем введения дополнительного бита четности происходит следующим образом. На передающей стороне передаваемый код анализируется и дополняется контрольным битом до четного или нечетного числа единиц в суммарном коде. Соответственно суммарный код называется четным или нечетным. В случае нечетного кода дополнительный бит формируется таким образом, чтобы сумма всех единиц в передаваемом коде, включая контрольный бит, была нечетной. При контроле четности все, естественно, наоборот. Например, в числе 0111 число единиц нечетно. Поэтому при контроле нечетности дополнительный бит должен быть нулем, а при контроле четности — единицей. На практике чаще всего используется контроль нечетности, поскольку он позволяет фиксировать полное пропадание информации (случай нулевого кода во всех информационных разрядах). На приемной стороне производится проверка кода четности. Если он правильный, то прием разрешается, в противном случае включается сигнализация ошибки или посылается передатчику запрос на повторную передачу.

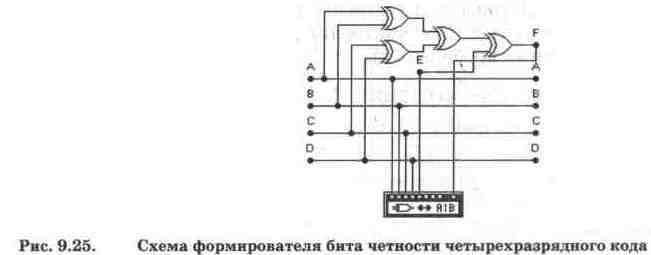
Схема формирования бита четности [8] для четырехразрядного кода показана на рис. 9.25. Она содержит четыре элемента Исключающее ИЛИ, выполняющих функции сумматоров по модулю 2 (без переноса) и состоит из трех ступеней. На первой ступени попарно суммируются все биты исходного кода на входах А, В, С, D. На второй ступени анализируются сигналы первой ступени и устанавливается четность или нечетность суммы входного кода. На третьей ступени полученный результат сравнивается с контрольным сигналом на входе Е, задающим вид используемого контроля, в результате чего на выходе F формируется пятый дополнительный бит четности, сопровождающий информационный сигнал в канале передачи.

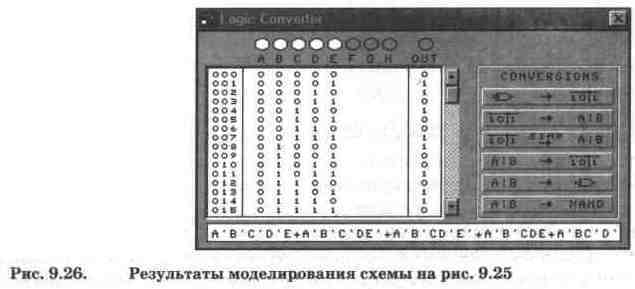
Результаты моделирования формирователя показаны на рис. 9.26 в виде таблицы истинности из 32 возможных двоичных комбинаций и булева выражения (из 32 комбинаций на рис. 9.26 видны только первые 16, остальные просматриваются с помощью линейки прокрутки). Для просмотра составляющих булева выражения необходимо мышью поместить курсор в дополнительный дисплей и передвигать его клавишами управления курсором.

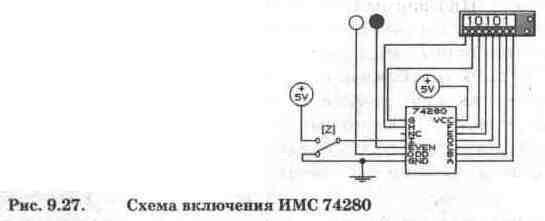
В библиотеке программы EWB схема проверки на четность и нечетность представлена ИМС 74280 (аналог — К555ИП5), схема ее включения показана на рис. 9.27. ИМС 74280 имеет 9 входов (A, B...I) и два выхода (EVEN, ODD), один из которых — инверсный. Вход I используется для управления видом контроля (0 — контроль четности, 1 — контроль нечетности) и управляется переключателем Z (управляется с клавиатуры одноименной клавишей). Вывод NC — not connection — пустой, т.е. внутри ИМС к нему ничего не подключено.

Правильность функционирования схемы на рис. 9.27 проверяется с помощью генератора слова, при этом тип контроля (четности или нечетности) выбирается переключателем Z; на входы рассматриваемого устройства подаются различные двоичные комбинации; состояние выходов ИМС контролируется подключенными к ним светоиндикаторами (логическими пробниками).

1. Какое назначение имеют формирователи кода четности, где они могут быть использованы?

2. Какая форма контроля четности чаще всего используется на практике, в частности, в Вашем компьютере, если в нем установлены модули ОЗУ с нечетным числом микросхем (см. разд. 5.12)?

3. Из представленных на экране логического преобразователя данных (рис. 9.26) выберите комбинации, относящиеся к контролю четности и нечетности, а также соответствующие им слагаемые булева выражения.

4. Проверьте правильность функционирования схемы на рис. 9.27, подавая на входы двоичные комбинации с генератора слова.

Знаете ли Вы, в чем ложность понятия "физический вакуум"?

Физический вакуум - понятие релятивистской квантовой физики, под ним там понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. Физическим вакуумом релятивистские теоретики называют полностью лишённое вещества пространство, заполненное неизмеряемым, а значит, лишь воображаемым полем. Такое состояние по мнению релятивистов не является абсолютной пустотой, но пространством, заполненным некими фантомными (виртуальными) частицами. Релятивистская квантовая теория поля утверждает, что, в согласии с принципом неопределённости Гейзенберга, в физическом вакууме постоянно рождаются и исчезают виртуальные, то есть кажущиеся (кому кажущиеся?), частицы: происходят так называемые нулевые колебания полей. Виртуальные частицы физического вакуума, а следовательно, он сам, по определению не имеют системы отсчета, так как в противном случае нарушался бы принцип относительности Эйнштейна, на котором основывается теория относительности (то есть стала бы возможной абсолютная система измерения с отсчетом от частиц физического вакуума, что в свою очередь однозначно опровергло бы принцип относительности, на котором постороена СТО). Таким образом, физический вакуум и его частицы не есть элементы физического мира, но лишь элементы теории относительности, которые существуют не в реальном мире, но лишь в релятивистских формулах, нарушая при этом принцип причинности (возникают и исчезают беспричинно), принцип объективности (виртуальные частицы можно считать в зависимсоти от желания теоретика либо существующими, либо не существующими), принцип фактической измеримости (не наблюдаемы, не имеют своей ИСО).

Когда тот или иной физик использует понятие "физический вакуум", он либо не понимает абсурдности этого термина, либо лукавит, являясь скрытым или явным приверженцем релятивистской идеологии.

Понять абсурдность этого понятия легче всего обратившись к истокам его возникновения. Рождено оно было Полем Дираком в 1930-х, когда стало ясно, что отрицание эфира в чистом виде, как это делал великий математик, но посредственный физик Анри Пуанкаре, уже нельзя. Слишком много фактов противоречит этому.

Для защиты релятивизма Поль Дирак ввел афизическое и алогичное понятие отрицательной энергии, а затем и существование "моря" двух компенсирующих друг друга энергий в вакууме - положительной и отрицательной, а также "моря" компенсирующих друг друга частиц - виртуальных (то есть кажущихся) электронов и позитронов в вакууме.

Однако такая постановка является внутренне противоречивой (виртуальные частицы ненаблюдаемы и их по произволу можно считать в одном случае отсутствующими, а в другом - присутствующими) и противоречащей релятивизму (то есть отрицанию эфира, так как при наличии таких частиц в вакууме релятивизм уже просто невозможен). Подробнее читайте в FAQ по эфирной физике.