Учет влияния нелинейностей в любой системе автоматического управления встречает большие трудности, поскольку приходится сталкиваться с решением нелинейных дифференциальных уравнений высоких порядков. В большинстве случаев учет нелинейностей не может быть выполнен в общем виде и позволяет пользоваться лишь частными решениями, выполняемыми с той или иной степенью приближения. Поэтому большую роль приобретают различные упрощенные и приближенные методы, при помощи которых можно получать ответы лишь на отдельные интересующие исследователей вопросы (устойчивость в определенных условиях, наличие автоколебаний, поведение системы в каком-либо частном режиме, например, при установившейся скорости, при трогании с места и т.п.).
В настоящее время разработано большое число приближенных методов исследования нелинейных систем автоматического управления. Дадим краткую характеристику тем из них, которые получили наибольшее распространение при решении практических задач.
Метод малых отклонений. Этот метод используется для исследования устойчивости систем по Ляпунову. При этом составляются уравнения для малых отклонений от состояния равновесия либо от установившегося движения, причем исследуется устойчивость данного состояния равновесия или данного движения. Если считать, что все отклонения достаточно малы, то можно пренебречь в первом приближении их высшими степенями и произведениями. Тогда получаются уравнения первого приближения, которые и могут быть подвергнуты исследованию на устойчивость при учете той или иной нелинейности.
Методы аппроксимации. В этом случае решение уравнений находят, заменяя характеристику нелинейного элемента некоторой близкой к ней кривой, которая может быть записана в аналитической форме.
Методы малого параметра. Метод возник в небесной механике в связи с решением задачи о трех телах. Основные исследования по этому методу принадлежат французскому математику Пуанкаре. В дальнейшем были разработаны различные варианты метода малого параметра, применяемые в радиотехнике и теории автоматического управления. Наиболее известными являются методы Ляпунова, Рэйля и Ван-дер-Поля. Метод последнего был строго обоснован Мандельштамом, Папалекси и Андроновым.
Общая идея метода малого параметра основана на том, что ряд членов, входящих в левую часть дифференциальных уравнений нелинейных систем, можно в ряде случаев считать малыми по сравнению с остальными членами, определяющими характер движения системы. Метод позволяет определить приближенные значения амплитуды и частоты основной гармоники периодических колебаний при гармонических возмущениях на входе системы, что позволяет рассчитать коэффициент усиления нелинейного звена по первой гармонике.
Численно-графические методы. Исследование нелинейной системы производится путем численных и графических способов интегрирования нелинейных дифференциальных уравнений, например, интегрирование по разностному методу Адамса—Штермера, способ приближенного интегрирования Чаплыгина, метод Эйлера, который является одним из наиболее простых методов. Он положен в основу почти всех графических способов, отличающихся друг от друга только по характеру геометрических построений. К более простым методам относятся метод секущих, метод касательных и метод с использованием решения уравнений в конечных разностях.
Метод фазовых траекторий. Метод основан на понятии фазового пространства. Он отличается наглядностью и возможностью получения полного представления характере возможных состояний системы. Сущность его заключается в следующем. Пусть система описывается дифференциальным уравнением n-го порядка. Ее состояние может быть задано п числами, определяющими координаты некоторой точки в га-мерном пространстве, причем каждой точке этого пространства будет соответствовать одно определенное состояние (определенная фаза) системы. Поэтому такое пространство называется фазовым. Для систем, описываемых дифференциальным уравнением второго порядка, фазовое пространство является двухмерным и в этом случае оно превращается в фазовую плоскость, на которой по двум осям координат (X,Y) откладываются какие-либо две переменные, характеризующие поведение данной системы в динамике (в переходном процессе). В качестве таких переменных чаще всего используется отклонение регулируемой величины Х (откладывается по оси X) и ее первая производная X', т.е. скорость изменения этого отклонения (откладывается по оси Y). В случае колебательного процесса с постоянными амплитудой и частотой, когда корни характеристического уравнения системы являются чисто мнимыми, изображение на фазовой плоскости будет представлять собой замкнутый контур — замкнутую фазовую траекторию, например, в виде эллипса. Каждому периоду колебаний соответствует прохождение изображающей точкой всего контура. В случае затухающего колебательного процесса (корни характеристического уравнения имеют отрицательную вещественную часть) изображение на фазовой плоскости будет иметь вид сходящейся к началу координат (или к определенному установившемуся значению при наличии внешнего возмущения) спиралевидной фазовой траектории и расходящейся — при расходящемся колебательном процессе (корни с положительной вещественной частью, система неустойчива).
Следует заметить, что фазовые траектории представляют собой геометрическое отражение процессов динамики в системе. В это отражение входят лишь координаты и отсутствует время. Поэтому фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы получить количественное положение изображающей точки в любой момент времени, нужно найти тем или иным способом решение переходного процесса во времени.
Методы моделирования. Являются наиболее эффективным средством анализа и синтеза, поскольку не требуют громоздких вычислений и графических построений, особенно в случае сложных нелинейных систем управления. Рассмотрим наиболее простые примеры систем, содержащих нелинейности релейного типа, рассмотренные в предыдущем разделе.
Модель потенциометрического датчика перемещения. Потенциометрические (реостатные) датчики широко применяются в системах управления и контроля, в частности, в уровнемерах (в том числе и бензобаках автомобилей), в которых поплавок связан с подвижным контактом, перемещающимся по виткам проволочного резистора. Перемещение подвижного контакта вызывает скачкообразное изменение сопротивления на величину сопротивления одного витка, что в общем случае является признаком наличия нелинейности в таком датчике.

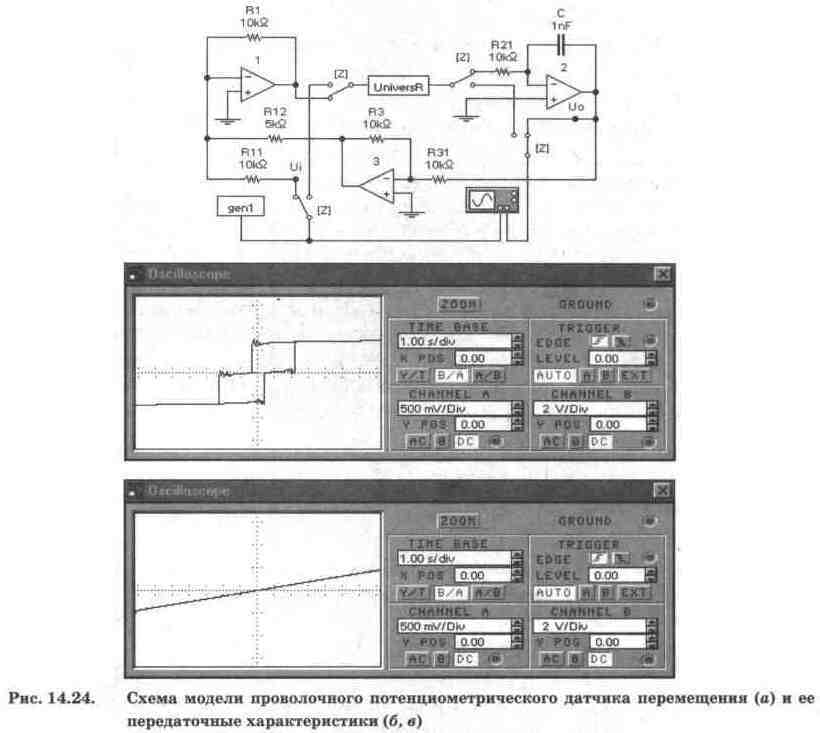
Схема модели потенциометрического датчика с использованием модели релейного элемента на рис. 14.21, а (для имитации скачкообразного изменения сопротивления при переходе подвижного контакта с витка на виток) показана на рис. 14.24, а [29]. Схема модели состоит из сумматора на ОУ 1, интегратора на ОУ 2, инвертирующего усилителя на ОУ 3, счетверенного переключателя Z, управляемого одноименной клавишей, и модели релейного звена (рис. 14.21, а), представленного подсхемой UniversR и имеющего передаточную характеристику, показанную на рис. 14.24, б. Характеристика получена при U1=U2=1 В, Кn=0,4 и С=100 пФ в положении переключателей Z, показанном на рис. 14.24, а.
Моделирование собственно потенциометрического датчика производится после перевода переключателей Z в положение, противоположное показанному на рис. 14.24, а. Результаты моделирования показаны на рис. 14.24, б, в. Полученная передаточная характеристика представляет собой многоступенчатую прямую линию. Согласно [29], величина ступеньки по горизонтали (входное напряжение Ui) равна UcpR11/R1, по вертикали (выходное напряжение Uo) — UcpR12R31/RlR3, скорость нарастания ступеньки — Us/CR21. Как следует из рис 14.24, б, напряжение срабатывания релейного элемента Ucp и напряжение срабатывания диодной цепочки Us примерно равны 1,1 и 2,4 В.
Релейная система автоматического регулирования [29]. Уравнение релейной системы задается в следующем виде:
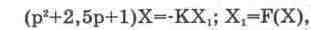 (14.22)
(14.22)
где p=d/dt — оператор дифференцирования.
Функция F(X) задается в виде передаточной функции на рис. 14.21, б с параметрами (в относительных единицах): напряжение срабатывания Ucр=1, напряжение отпускания Uoтп=0,6, выходная амплитуда (напряжение срабатывания диодной цепочки) Us=1. Задачей моделирования является определение характера переходных процессов при начальных условиях Х(0)=1, Х'(0)=0 и следующих значениях коэффициента К: 304, 400, 200 и 100.
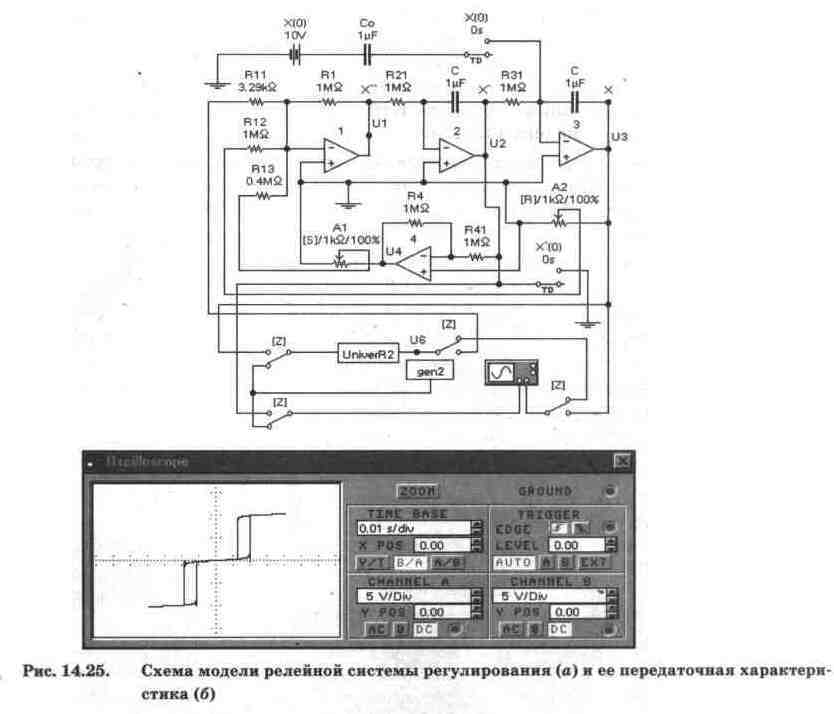
Схема модели приведена на рис. 14.25, а. Ее параметры выбираются таким же образом, как и в разделе 14.1. Начнем с составления уравнений для выходного напряжения каждого блока. В данном случае они будут определяться выражениями:
О для сумматора на ОУ 1 U1=-(K11-U6+K12-A2-U3+K13.A1-U4);
О для первого интегратора на ОУ 2 U2=-K21-Ul/p;
О для второго интегратора на ОУ 3 U3=-K31-U2/p;
О для масштабирующего усилителя на ОУ 4 U4=-K41-U2;
О для релейного элемента U6=-F(U3).
С помощью приведенных формул получаем:
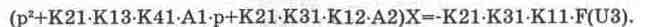
После преобразования переменных путем введения масштабов X=MxU3 и X1=M1xU6 будем иметь:
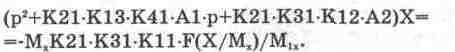 (14.23)
(14.23)
Примем Mx=X(0)/U3=1/10=0,1 и Мx=М1x=0,1. В таком случае из сопоставле ния исходного (14.22) и машинного (14.23) уравнений получаем выражения для вы бора параметров модели в следующем виде:
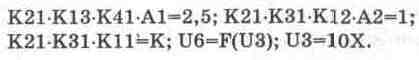 (14.24)
(14.24)
Задаемся значениями коэффициентов передачи К12=К41=1, что соответствует выбору сопротивлений резисторов R1=R12=R4=R41=1 MOM. Задаемся также значениями коэффициентов деления делителей А1=А2=1 на потенциометрах с одноименными позиционными обозначениями (установлены на 100%) и коэффициентами передачи К21=К31=1 с, что при С=1 мкФ соответствует выбору сопротивлений резисторов R21=R31=1 МОм. При указанном выборе для обеспечения коэффициента 2,5 в уравнении (14.22) коэффициент передачи К13 должен быть равен, как следует из условий (14.24), 2,5, т.е. сопротивление резистора R13=1/2,5=0,4 МОм. Для обеспечения заданного значения коэффициента К=304 сопротивление резистора R11 должно быть равно R1/304=3,29 кОм, для К=400 — 2,5 кОм, для К=200 — 5 кОм, для К=100 — 10 кОм. Для введения начального условия Х(0)=10 В (с учетом принятого масштаба) в схеме используется источник заряда, образованный источником постоянного напряжения Х(0) и конденсатором Со и подключаемый на короткое время (0,06 с) после запуска моделирования ко входу интегратора на ОУ 2 с помощью программного переключателя Х(0), установленные параметры которого Топ=0 и Toff =0,06 с выбраны опытным путем из условия обеспечения Х(0)=10 В за минимально возможное короткое время. Введение условия Х'(0) достигается закорачиванием на короткое время (0,06 с) после пуска выхода ОУ 2 на общую шину с помощью программного переключателя Х'(0), параметры которого выбраны аналогичными переключателю Х(0).
В качестве релейного элемента в схеме на рис. 14.25, а использована схема на рис. 14.21, а, оформленная в виде подсхемы UniverR2 и имеющая, согласно условиям задачи и принятому масштабу, следующие параметры (см. рис. 14.25, б): напряжение срабатывания Ucp=10 В, напряжение отпускания Uотп=6 В, выходное напряжение (напряжение срабатывания диодной цепочки) Us=10 В. Для обеспечения такого значения U. напряжение стабилизации стабилитронов было установлено равным 5,5В. Для возможности оперативного изменения параметров модели релейного элемента и наблюдения ее передаточной характеристики в схеме на рис. 14.25, а предусмотрен счетверенный переключатель Z, показанный в положении контроля релейного элемента, и генератор одиночного треугольного сигнала gen2, отличающийся от gen1 только тем, что в нем установлено U1=U2=10 В (см. схему на рис. 14.14, а).
Для проведения моделирования переключатель Z нажатием клавиши Z необходимо перевести в противоположное показанному на рис. 14.25, а положение. При этом на входы осциллографа подаются сигналы Х (канал В, ось Х прямоугольных координат) и ее первая производная X' (канал А, ось Y), т.е. на экране осциллографа мы получаем фазовую траекторию (или фазовый портрет) исследуемой системы, которая для различных значений коэффициента К показана на рис. 14.26.
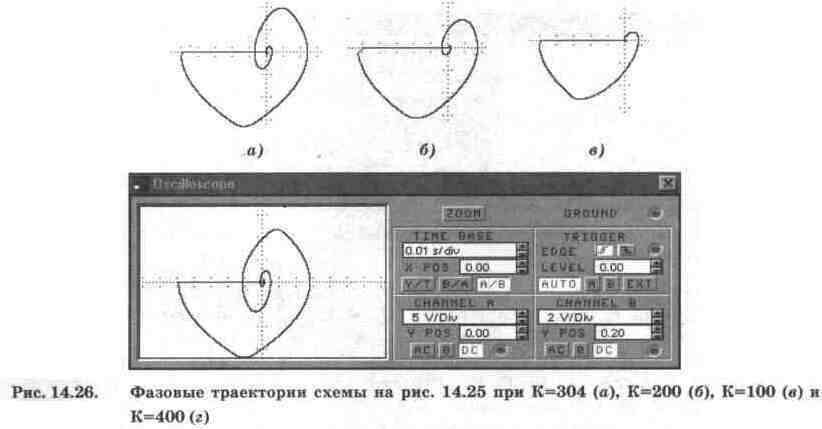
Из рис. 14.26 видно, что для всех значений К фазовые траектории имеют вид сходящихся к началу координат спиралей. Следовательно, переходной процесс в рассматриваемой системе носит затухающий колебательный характер, причем размах колебаний и, следовательно, длительность переходного процесса уменьшается с уменьшением коэффициента К, определяющего влияние релейного элемента.
Контрольные вопросы и задания
1. В чем заключается основное различие между линейными и нелинейными системами автоматического регулирования?
2. Назовите приближенные методы анализа автоматических систем. В чем заключается сущность метода фазовых траекторий?
3. Какой тип нелинейности используется при моделировании потенциометричес-кого датчика перемещения?
4. Какие функции выполняют решающие блоки на ОУ 2 и 3 в модели потенциоме-трического датчика?
5. Если выбрать коэффициент деления А2=0,5 на одноименном потенциометре, то как это скажется на выборе коэффициентов передачи других блоков в схеме на рис. 14.25, а?
6. Если из схемы на рис. 14.25, а исключить устройства для ввода начальных условий (Х(0) и Х'(0)), то как это скажется на результатах моделирования? Ответ проверьте на модели.
7. Отключите в схеме на рис. 14.25, а устройства ввода начальных условий. Подключите к суммирующему узлу сумматора на ОУ 1 через резистор R14=1 MOM источник постоянного напряжения. Установите зависимость фазовых траекторий схемы при К=100 и 400 от напряжения подключенного источника, выбрав его равным 1, 3, 10 и 12 В.
8. К схеме на рис. 14.3 осциллограф подключите таким образом, чтобы можно было получать ее фазовый портрет (фазовые траектории). Проведите сравнительный анализ фазовых траекторий для этой схемы при колебательном и апериодическом переходном процессе.
9. В некоторых случаях задаваемые параметры моделирования (например, коэффициент К в схеме на рис. 14.25, а) могут меняться в достаточно широких пределах, что может привести к дополнительной нелинейности в виде насыщения ОУ. Для предотвращения таких явлений используют масштабирование не только по напряжению, но и по времени. Для примера для схемы на рис. 14.25, а введем масштаб времени Mt=t/T=l/3. В этом случае в уравнении (14.22) оператор p=d/dt станет равным 3(d/dT), а само уравнение, разрешенное относительно старшей производной, примет следующий вид:
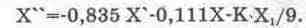
В таком случае первые три условия из (14.24) запишутся следующим образом:
 (14.25)
(14.25)
Используя выражения (14.25), выберите коэффициенты передачи для схемы на рис. 14.25, а и проведите моделирование при указанных выше значениях коэффициента К. Полученные результаты сравните с данными, приведенными на рис. 14.26.
10. Измерьте время моделирования от момента пуска до момента прихода отображающей точки фазовой траектории в начало координат для указанных значений коэффициента К. Для измерения времени воспользуйтесь счетчиком, табло которого находится рядом с выключателем и который запускается одновременно с запуском моделирования. Для получения отсчета в секундах показания счетчика необходимо умножить примерно на 10. Полагая, что измеренное таким образом время определяет время переходных процессов, определите, при каком значении коэффициента К оно минимально.
|
|