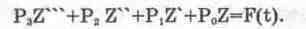 (14.1)
(14.1)
Поскольку моделирование автоматических систем управления чаще всего сводится к решению дифференциальных уравнений, то в первую очередь рассмотрим устройства для их решения, которые в аналоговой вычислительной технике часто называют дифференциальными анализаторами.
В дифференциальных анализаторах реализуются два метода интегрирования дифференциальных уравнений. Один из них основан на повышении порядка производных искомой функции, а другой — на его понижении [29, 61]. Рассмотрим их на примере линейного дифференциального уравнения с постоянными коэффициентами третьего порядка
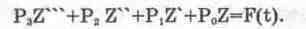 (14.1)
(14.1)
Для интегрирования дифференциального уравнения методом повышения порядка производных его необходимо решить относительно производной неизвестной функции Z низшего порядка. Приняв Z за производную нулевого порядка, из (14.1) получим
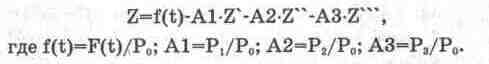 (14.2)
(14.2)
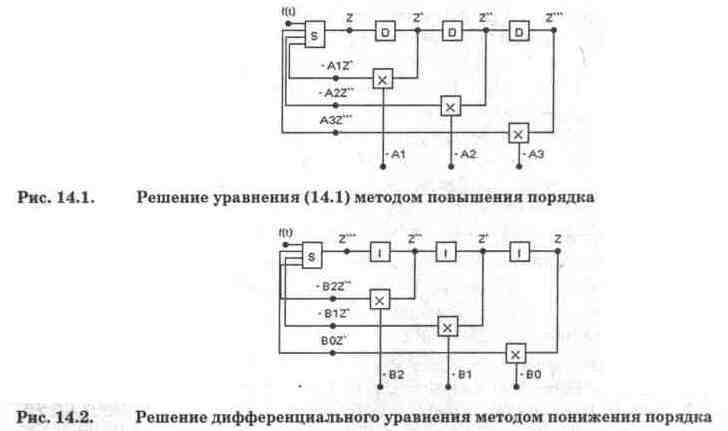
Структурная схема модели для решения уравнения (14.2) показана на рис. 14.1. Из формулы (14.2) следует, что для получения переменной Z необходимы следующие вычислительные блоки: 4-входовой сумматор (блок S на рис. 14.1), три дифференциатора (блоки D) и три умножителя (блоки X) для умножения на коэффициенты AL Выходной сигнал сумматора, обозначенный на схеме рис. 14.1 буквой Z, будет искомым решением уравнения (14.1).
Отметим, что метод повышения порядка производных почти не применяется на практике, так как дифференцирующие блоки весьма чувствительны к помехам (см. гл. 10), которые могут стать источником ошибок. Например, если в электронной вычислительной машине возмущение f(t) подается на суммирующий блок от функционального потенциометра, то фактически оно будет изменяться не плавно, а сту-пенчато при переходе подвижного контакта от одного витка потенциометра к другому, что будет регистрироваться дифференцирующими блоками в виде значительных всплесков напряжения. Значительные ошибки в определении мгновенного значения производной имеют место и в точках перехода от одной аппроксимирующей прямой к другой, при вводе возмущения от диодного функционального аппроксиматора и т.п. Метод повышения порядка производных используется только в тех случаях, когда без него нельзя обойтись, например, в специализированных вычислительных машинах. Однако в этом случае используются специальные дифференцирующие устройства, вырабатывающие не мгновенные, а усредненные (сглаженные) значения производных.
Для интегрирования уравнения (14.1) методом понижения порядка производных его нужно решить относительно производной функции Z(t) высшего порядка, т.е.
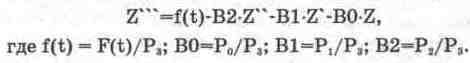 (14.3)
(14.3)
Структурная схема модели для этого случая показана на рис. 14.2. Из формулы (14.3) видно, что для получения переменной Z необходимы следующие вычислительные блоки: 4-входовой сумматор (блок S на рис. 14.2), три интегратора (блоки I) и три умножителя (блоки X) для введения коэффициентов Bi. Выходной сигнал третьего интегратора, обозначенный на схеме рис. 14.2 буквой Z, будет искомым решением уравнения (14.3).
Достоинством метода понижения порядка, нашедшего наибольшее распространение на практике, является высокая точность, обусловленная применением интеграторов, что устраняет в определенной мере влияние различных флуктуаций, возникающих в схеме.
По конструктивному выполнению моделирующие устройства делятся на матричные и структурные. Устройства матричного типа представляют собой конструктивно законченные наборы из разных вычислительных блоков, каждый из которых позволяет моделировать одно из уравнений системы дифференциальных уравнений.
Такие устройства являются достаточно специализированными и в нашем случае не представляют интереса. Устройства структурного типа реализуют решение дифференциальных уравнений и их систем в том виде, в каком они заданы. Они представляют собой наборы простейших вычислительных блоков, соединяемых между собой определенным образом в зависимости от вида дифференциального уравнения высокого порядка или системы дифференциальных уравнений первого порядка, и уступают матричным только по оперативности набора подготовленных к решению задач.
В общем случае процесс решения дифференциального уравнения путем моделирования состоит из следующих этапов:
1) приведение дифференциального уравнения к виду, удобному для моделирования;
при этом исходное уравнение, подлежащее воспроизведению, называют моделируемым, а уравнение, описывающее связь между входными и выходными величинами моделирующего устройства — моделирующим или машинным уравнением;
2) выбор масштабов машинного уравнения; под масштабами понимаются отношения математических величин к воспроизводящим их физическим величинам;
если некоторая математическая переменная величина Х изображается физической величиной, например, напряжением U, то масштаб К, величины Х (или масштаб Кц величины U) определяется выражением Kх,=Ku=X/U, т.е. масштаб представляет собой число единиц математической величины, соответствующее одной единице физической величины, моделирующей первую;
3) соединение вычислительных блоков для воспроизведения машинного уравнения (в EWB — подготовка схемы модели);
4) проведение моделирования с регистрацией результатов с последующим переходом при помощи ранее выбранных масштабов от переменных величин модели к переменным величинам моделируемой системы-оригинала.
Перечисленные этапы часто относят к так называемому методу моделирования по уравнению. Он позволяет не только решать различные уравнения, но и исследовать системы автоматического управления, для которых уже заранее выбраны все параметры звеньев. Дальнейшим развитием этого метода является метод структурного моделирования, который позволяет решать более сложные задачи выбора параметров структурных звеньев системы-оригинала (см. разд. 14.5).
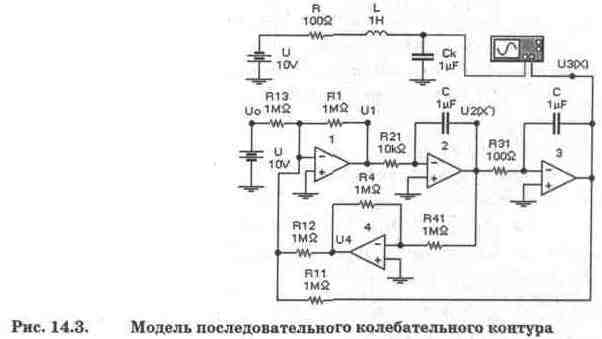
В качестве примера рассмотрим моделирование последовательного колебательного контура, показанного в верхней части рис. 14.3 и состоящего из катушки индуктивности L с активным сопротивлением R и конденсатора Ck. В нижней части рис. 14.3 изображена электронная модель этого же контура на решающих элементах: сумматоре на ОУ 1, двух интеграторах на ОУ 2 и 3 и инвертирующем усилителе на ОУ 4. Позиционное обозначение резисторов принято в соответствии с рекомендациями [29]: порядковый номер резистора в цепи обратной связи совпадает с номером ОУ, токозадающие резисторы имеют двухзначный номер, первым идет номер соответствующего ОУ, вторым — порядковый номер резистора данной группы. Для конденсаторов интеграторов можно использовать такой же принцип формирования позиционных обозначений, однако в связи с тем, что, как правило, в интеграторах моделирующих установок они имеют одинаковое номинальное значение (в данном случае 1мкФ), то они имеют и одинаковое позиционное обозначение. При обозначении выходных напряжений решающих элементов используется тот же принцип, для наглядности в скобках указывается также и номер соответствующей производной. Для регистрации результатов моделирования в схеме на рис. 14.3 используется осциллограф: канал А — для регистрации напряжения на конденсаторе Ck, канал В — для регистрации напряжения на выходе модели. В качестве источника возмущающего сигнала в рассматриваемом случае используется источник постоянного напряжения U, однако в общем случае это может быть любая функция времени.
Запишем дифференциальное уравнение колебательного контура в следующем виде:
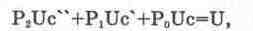 (14.4)
(14.4)
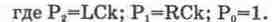
Приведем уравнение (14.4) к виду (14.3)
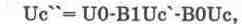 (14.5)
(14.5)
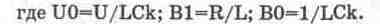
Как следует из (14.5),.модель колебательного контура должна содержать сумматор (в схеме на рис. 14.3 он выполнен на ОУ 1) и два интегратора (ОУ 2,3). Поскольку сигнал на выходе ОУ 2 имеет полярность, совпадающую с полярностью сигнала на входе сумматора на ОУ 1, то для обеспечения устойчивости модели выход интегратора на ОУ 2 соединен со входом сумматора через инвертирующий усилитель на ОУ 4.
Составим уравнения для каждого решающего блока:
для сумматора
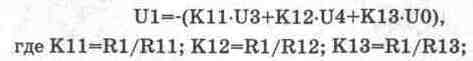 (14.6)
(14.6)
для первого интегратора
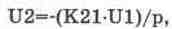 (14.7)
(14.7)
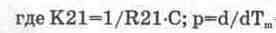 — оператор дифференцирования;
Тm — независимая переменная — время;
— оператор дифференцирования;
Тm — независимая переменная — время;
для второго интегратора
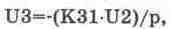 (14.8)
(14.8)
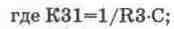
для инвертирующего усилителя
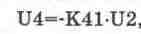 (14.9)
(14.9)
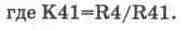
Разрешая систему уравнений (14.6) — (14.9) относительно величины U3, являющейся в данном случае искомой, получим:
 (14.10)
(14.10)
В общем случае величина U3 может представлять исходную переменную (в данном случае — напряжение на конденсаторе Ck) в некотором масштабе, то же самое относится и к независимой переменной (времени) и возмущающему воздействию Uo. Поэтому в уравнение (14.10) необходимо ввести масштабные коэффициенты, которые определяются очевидными уравнениями преобразования:
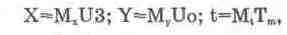 (14.11)
(14.11)
где М„ — масштаб представления искомой величины Х в виде напряжения; My — масштаб представления возмущающего воздействия Uo; М, — масштаб времени.
С учетом соотношений (14.11) уравнение (14.10) запишется в виде:
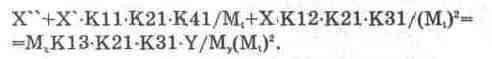 (14.12)
(14.12)
В таком же виде запишем исходное уравнение (14.4):
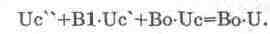 (14.13).
(14.13).
Очевидно, что из условия идентичности оригинала и его модели коэффициенты при соответствующих переменных в уравнениях (14.12) и (14.13) должны быть одинаковыми, т.е.
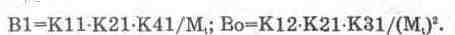
(14.14)
Из сравнения коэффициентов в правой части каждого уравнения следует требование Мх=Му. Кроме того, из схемы на рис. 14.3 видно, что K11=K12=K13=K41=1. Примем для упрощения последующих расчетов Mt=l. В таком случае условия (14.14) запишем в следующем виде: K21=R/L; K21-K31=l/(LCk) или с учетом обозначений для К21 и К31
R21=L/RC; R31=RCk/C. (14.15)
Выражения (14.15) позволяют выбрать параметры интеграторов модели с использованием параметров оригинала. При указанных на схеме номинальных значениях этих параметров получаем R21=10 кОм и R31=100 Ом.
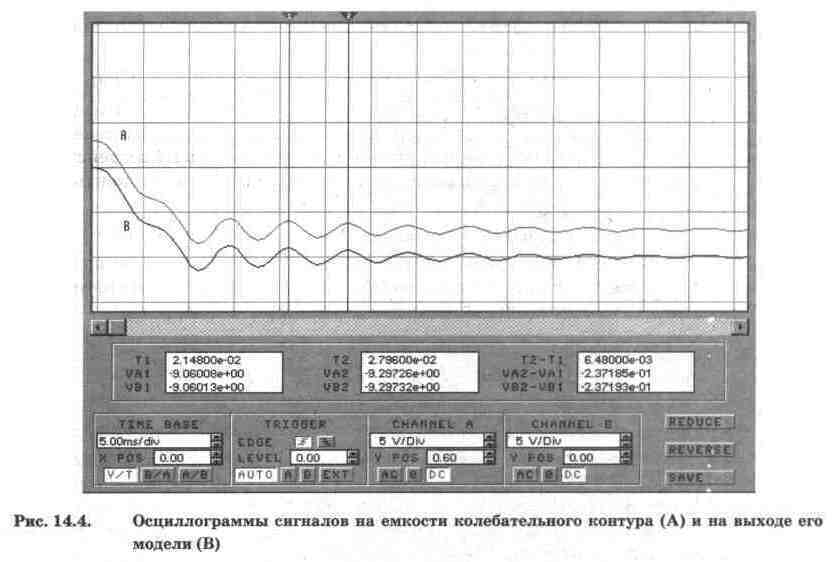
Перед проведением моделирования необходимо включить режим анализа переходных процессов и установить опцию для паузы после заполнения экрана осциллографа (меню Circuit/Analysis Options). Результаты моделирования показаны на рис. 14.4, откуда видно, что форма и амплитуда сигналов на емкости конденсатора Ск колебательного контура и на выходе его модели совпадают. Из рис. 14.4 видно также, что период затухающих колебаний колебательного переходного процесса равен Т=Т2-Т1=6,48 мс близок к расчетному с использованием формулы
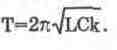
Контрольные вопросы я задания
1. В чем заключается различие между физическим и математическим моделированием?
2. Какие средства вычислительной техники могут быть использованы при математическом моделировании?
3. Какие методы решения дифференциальных уравнений используются при их моделировании с помощью EWB?
4. Что такое "структурное моделирование" и моделирование "по уравнению"? Какой метод использован при подготовке модели на рис. 14.1.
5. Из сравнения рис. 14.2 и 14.3 установите, каким образом в моделях вводятся коэффициенты дифференциального уравнения (в частности, коэффициенты В1 и ВО)? Обязательно ли при этом использование перемножающих устройств?
6. Из осциллограмм на рис.
14.4 видно, что переходной процесс в резонансном контуре имеет колебательный
характер. Известно (это следует из решения уравнения (14.13)), что вид переходного
процесса в колебательном контуре определяется
соотношениями 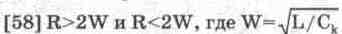 — волновое сопротивление
контура. Установите, какое из приведенных соотношений соответствует колебательному
переходному процессу, а какое — апериодическому. Для последнего случая рассчитайте
параметры интеграторов, используя формулы (14.15), и проведите моделирование.
— волновое сопротивление
контура. Установите, какое из приведенных соотношений соответствует колебательному
переходному процессу, а какое — апериодическому. Для последнего случая рассчитайте
параметры интеграторов, используя формулы (14.15), и проведите моделирование.
7. В модели на рис. 14.3 источник постоянного напряжения U замените на источник переменного напряжения с амплитудой 1 В и частотой, равной резонансной частоте контура, и проведите моделирование.
|
|