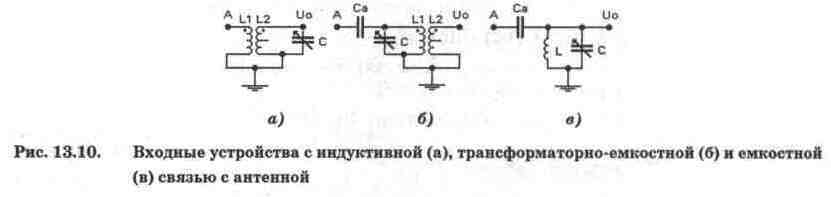
Входные устройства (ВУ, их называют еще преселекторами) радиоприемных устройств представляют собой резонансную систему, схема которой определяется типами связи с антенной и с первым каскадом приемника (рис. 13.10).
Входное устройство по схеме рис. 13.10, а рассчитано на применение в первом каскаде приемника резонансного усилителя с достаточно высоким входным сопротивлением (каскад на полевом транзисторе), катушка L1 в этом случае носит название катушки связи, если L1 и L2 намотаны на одном каркасе.
Входное устройство на рис. 13.10, б характерно для приемников с магнитной антенной и возможностью подключения дополнительно внешней антенны (через конденсатор Са) при трансформаторной связи с первым каскадом приемника. Отметим, что с целью минимизации влияния входного сопротивления этого каскада на избирательные характеристики резонансного контура емкость конденсатора связи Са с антенной выбирается достаточно малой.
Входное устройство на рис. 13.10, в является наиболее простым и широко используемым практически на всех диапазонах; при необходимости согласования со входным каскадом приемника от катушки L делается отвод, который подключается ко входному каскаду (автотрансформаторная связь с нагрузкой).
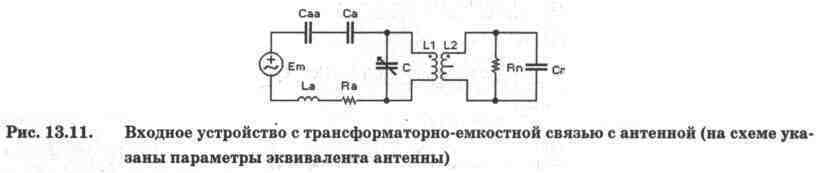
Рассмотрим эквивалентную схему ВУ с трансформаторно-емкостной связью с антенной на рис. 13.11, на котором обозначено: La, Caa, Ra — эквивалентная индуктивность, емкость и активное сопротивление антенны, Em — ЭДС, наводимая в антенне.
Как правило, в диапазоне частот вплоть до ультракоротких волн индуктивное и активное сопротивление антенны значительно меньше емкостного [55], что позволяет упростить схему на рис. 13.11 и привести ее к виду, показанному на рис. 13.12, на котором Со=Саа-Са/(Саа +Са); Le — индуктивность рассеяния первичной обмотки трансформатора (устанавливается в диалоговом окне параметров трансформатора); Сn'=n2Cn — приведенная к первичной обмотке емкость нагрузки Cn [50], где n — коэффициент трансформации, задаваемый в окне параметров трансформатора. Сопротивление Rk, состоит из активного сопротивления первичной обмотки трансформатора Rp, которое устанавливается в окне его параметров и по умолчанию равно нулю, и эквивалентного сопротивления нагрузки Rn'=n2Rn [50], пересчитанному параллельно контуру. Для преобразования его в последовательно включенное, что более удобно для дальнейшего анализа, используется формула
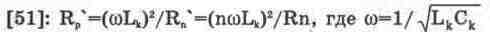— резонансная частота
контура;
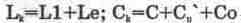. Таким образом,
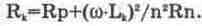
Поскольку, как указывалось выше, емкость конденсатора связи Са выбирается достаточно малой, ток, поступающий в параллельный колебательный контур, образованный элементами Сn', С, Le, L1 и Rn', равен
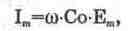(13.1)
При резонансе ток Im' в индуктивной или емкостной ветви параллельного колебательного контура равен [56]
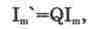(13.2)
где
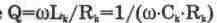— добротность контура.
После подстановки (13.1) в (13.2) получим
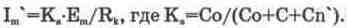
Напряжение на первичной обмотке трансформатора
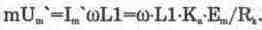
Напряжение на выходе устройства (на вторичной обмотке трансформатора)
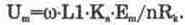
, Следовательно, коэффициент передачи входного устройства равен
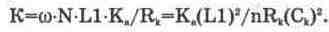(13.3)
Пренебрегая индуктивностью рассеяния, т.е. выбирая в окне параметров трансформатора Le=0, рассмотрим два случая:
1) активное сопротивление первичной обмотки Rp = О;
2) активное сопротивление значительно больше эквивалентного сопротивления нагрузки.
В первом случае
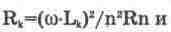
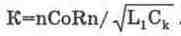(13.4)
Во втором случае Rp>>Rp' следовательно, Rk=Rp и
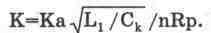(13.5)
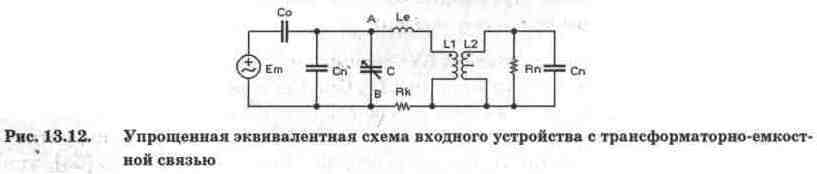
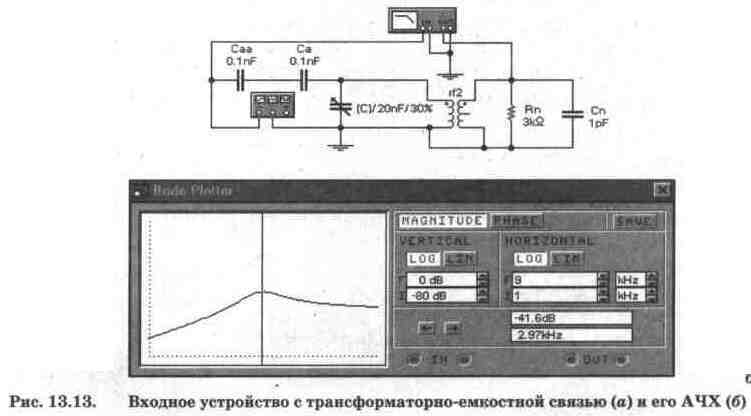
Перейдем к моделированию ВУ, показанного на рис. 13.13, а, для которого приняты следующие значения параметров трансформатора: Rp=0 и п=3. При остальных параметрах, указанных на схеме, расчеты по формуле (13.4) дают
Результаты моделирования показаны на рис. 13.13, б, откуда видно, что коэффициент передачи составляет -41,6 дБ, что весьма близко к расчетному. Отметим, что расчетное значение резонансной частоты — 2,9 кГц — также близко к полученному при моделировании.
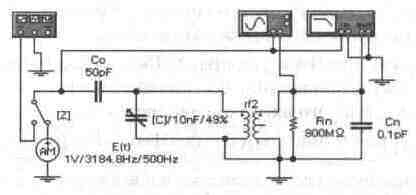
Перейдем к рассмотрению процесса прохождения через ВУ (рис. 13.14, а) АМ-сигналов. При моделировании используется источник АМ-сигнала
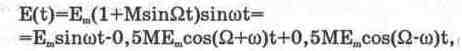(13.6)
где Еm — амплитуда несущей; М<1 — коэффициент модуляции;
Переключатель Z позволяет подключиться к функциональному генератору для оперативного получения АЧХ входного устройства.
Как видно из выражения (13.6), спектр АМ-сигнала состоит из трех компонентов: несущей и двух боковых колебаний. Для случая настройки колебательного контура на частоту сигнала ток на его входе определяется выражением [51]:
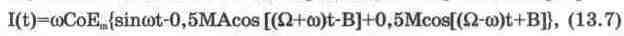
где
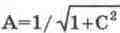— коэффициент уменьшения
модуляции;
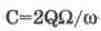— абсолютная
величина обобщенной расстройки
для верхней и нижней боковых частот;
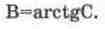
Из выражения (13.7) видно, что на верхней боковой частоте ток запаздывает, а на нижней он опережает напряжение на угол В, при этом коэффициент модуляции
уменьшается в соответствии с выражением:
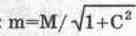
Попробуем воспользоваться приведенными формулами для расчета параметров выходного АМ-сигнала со следующими исходными данными (кроме показанных на рис. 13.14,
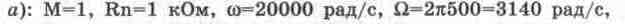
Lk=0,5 Гн, Ck=5 нФ, контур настроен на несущую частоту. В результате расчетов получаем: Q=0,5 20000/1000=10; С=2 10-3140/20000=3,14; B=arctg3,14=72,33°;
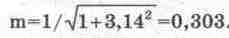
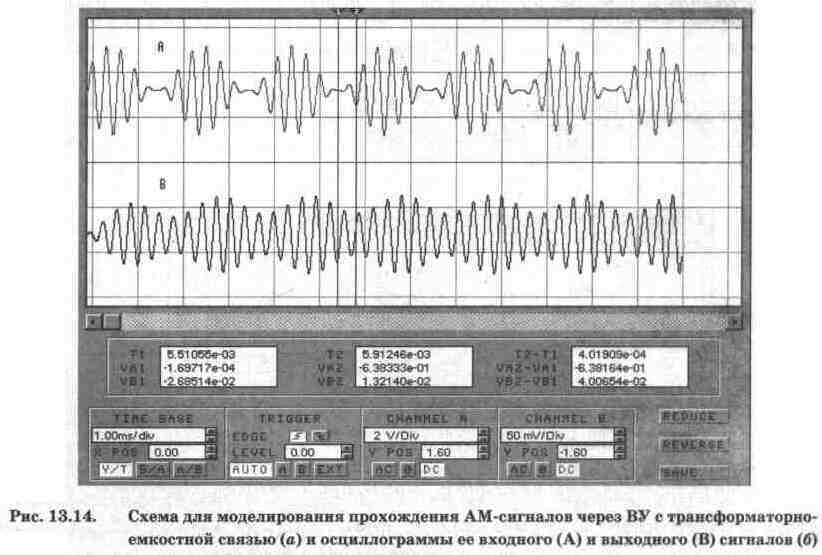
Результаты моделирования показаны на рис. 13.14, б, откуда видно, что временной интервал Т2-Т1, характеризующий фазовый сдвиг выходного сигнала, составляет около 0,4 мс, что при периоде модулирующей частоты 2 мс соответствует примерно 72°, т.е. близко к расчетному.
Контрольные вопросы и задания
1. Проведите моделирование ВУ на рис. 13.13, а при Rp=l кОм и Rn=1000 МОм и сравните полученные результаты с расчетными по формуле (13.5).
2. При расчетах зависимости резонансной частоты и коэффициента передачи ВУ по формуле (13.5) от емкости нагрузки Сп получены, в частности, следующие ре-
Результаты (цифры в скобках относятся к результатам моделирования): при Сп=1нФ К = -32,26 дБ (-31,9 дБ), F = 2,87 кГц (2,87 кГц); при Сп=10 нФ К = -34,2 дБ (-31,6 дБ), F = 2,66 кГц (2,66 кГц). Из приведенных данных видно, что если результаты расчета и моделирования по определению резонансной частоты совпадают, то по коэффициенту передачи они заметно отличаются. Причем, если расчетные значения К с ростом Сп уменьшаются, то при моделировании они, наоборот, увеличиваются. Чем объяснить такое явление и имеет ли оно практическое значение?
3. Используя схему на рис. 13.13, а при Rn>>Rp=l кОм, на основании выражения (13.3) рассчитайте зависимость резонансной частоты и коэффициента передачи ВУ от индуктивности рассеяния Le. Сопоставляя результаты расчета с результатами моделирования, установите правомерность включения индуктивности Le в соответствии с эквивалентной схемой на рис. 13.12.
4. Используя модель на рис. 13.14, а, исследуйте зависимость фазового угла и формы выходного сигнала от частоты модулирующего сигнала в диапазоне частот от 10 до 800 Гц.
5. Используя выражение (13.7), по аналогии с методикой получения формулы (13.3) получите выражение для коэффициента передачи ВУ для АМ-колебаний.
6. Используя методику, изложенную в разд. 13.5, определите коэффициент модуляции AM колебания на рис. 13.14, б и сравните с расчетным значением.
|
|
 |
