Упражнения
Методические указания Методику расчета и экспериментального исследования процессов в сложных цепях с одним реактивным элементом рассмотрим на конкретных примерах, включающих задачи на постоянное и гармоническое воздействие. Задача 1. Подключение конденсатора к неидеальному источнику постоянной ЭДС.
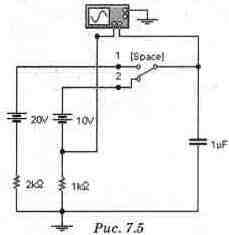
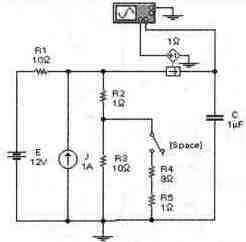
Рассчитать напряжение uc (t) и ток конденсатора ic (t) при переключении ключа [Space] в схеме, приведенной на рис. 7. 5 (файл с7_11). При расчете принять, что переключения происходят из установившихся режимов. Проверить результаты расчетов с помощью Electronics Workbench. Считать, что ключ [Space] в положении 1 включен (замкнут), а в положении 2 - выключен (разомкнут).
Расчет Шаг 1. Применим общую формулу (7. 9) для расчета напряжения на конденсаторе:
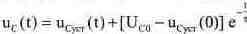
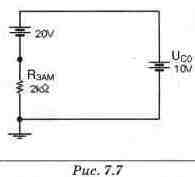
где т = RC - постоянная времени цепи, Uco - начальное напряжение на конденсаторе, Uсчст (t) - напряжение на конденсаторе в установившемся режиме. В соответствии с законом коммутации напряжение на конденсаторе в момент коммутации не изменяется. Поэтому установившееся значение напряжения на конденсаторе при разомкнутом ключе и будет начальным напряжением Uco на нем при замыкании ключа. На рис. 7. 6 изображена схема замещения при разомкнутом ключе. В этой схеме замещения напряжение на конденсаторе установится, когда потенциалы конденсатора и источника сравняются, а напряжение на резисторе и ток через него станут равными нулю. Следовательно, Uyстp= Uco= Ераэ=10 В. Шаг 2. Теперь необходимо найти значение тока в момент t = 0+. Для вычисления значений параметров переходного процесса конденсатор можно заменить источником постоянной ЭДС с выходным напряжением равным Ucoз. При этом получим схему замещения, представленную на рис. 7.7.
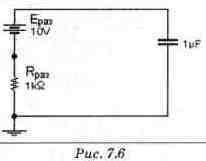
Из схемы рис. 7.7:
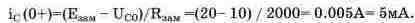
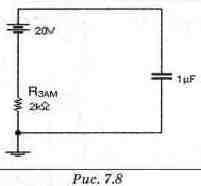
Шаг 3. Определим установившееся значение напряжения UcycT при замкнутом ключе (рис. 7.8). Поскольку схемы рис. 7.6 и 7.8 идентичны по структуре, установившиеся значения определяются сходным образом: исуст^эаи^О В. Поскольку при замыкании ключа ток ограничивается сопротивлением Raa»i> постоянная времени цепи равна Тз= КэамС= 2 мс. Из выражения (7.9) следует,что:
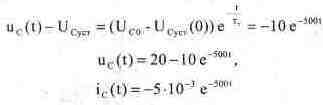
Шаги 4, 5, 6. Для случая размыкания ключа Ucycтp= = Ераз = 10 В, Uco=Eзам. Предоставим читателю возможность самому разобраться в том, какие схемы замещения и условия необходимо применить, чтобы получить приведенные ниже уравнения для тока и напряжения при размыкании ключа.
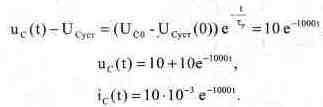
Экспериментальная проверка результатов расчета Экспериментальная проверка полученных результатов заключается в измерении величин, характеризующих изменения тока и напряжения конденсатора при замыкании и размыкании ключа. Покажем, как экспериментально определяются четыре величины, относящиеся к размыканию ключа. Измерить их можно по единственной осциллограмме, полученной в схеме рис. 7.9(файл с7_11). Для получения такой осциллограммы необходимо, прежде всего, правильно собрать схему измерений. Общий вывод осциллографа и один из узлов исследуемой схемы нужно заземлить. Для измерения тока можно использовать резистор, включенный в исследуемую ветвь и подсоединенный одним выводом к земле, как это сделано в схеме рис. 7.9а. Однако это не всегда удобно, и лучше измерять ток с помощью универсального датчика тока, каким является источник напряжения, управляемый током (о схеме включения его см. Приложение 1). Напряжение на конденсаторе можно наблюдать непосредственно только в случае, когда один из его выводов также подсоединен к земле. Имеется, однако, возможность исключить это ограничение, пользуясь универсальным датчиком напряжения. В качестве его применяется источник напряжения, управляемый напряжением (схема его подключения приведена в Приложении 1).
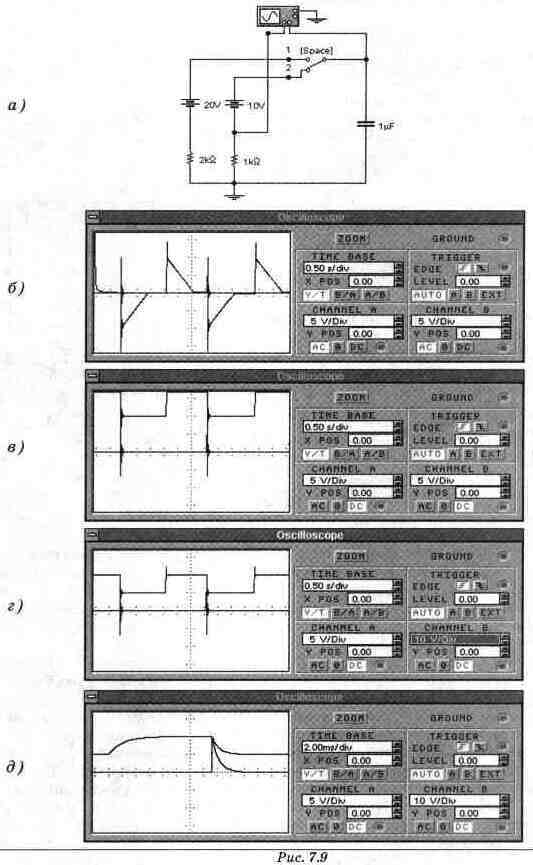
Кроме того, очень важна точная настройка осциллографа. Мы рекомендуем читателю прежде, чем приступить к эксперименту, ознакомиться с методикой измерения мгновенных значений напряжения с помощью осциллографа, изложенной в Приложении 1. К чему может привести измерение ненастроенным осциллографом, проиллюстрируем на примере. На рис. 7,9 приведены осциллограммы, получающиеся после каждого шага настройки осциллографа, начиная от настройки по умолчанию. 1. Первая некорректность исходной настройки, которой соответствует осциллограмма на рис. 7.96, заключается в том, что оба канала переведены в режим АС. В уравнениях для переходных процессов присутствуют постоянные составляющие, и чтобы их увидеть, необходимо перевести оба канала А и В осциллографа в режим DC. На рис. 7.9в настройка режима исправлена. 2. Другая некорректность настройки заключается в том, что осциллограмма напряжения на конденсаторе выходит за верхнюю границу экрана (рис. 7.9в). Необходимо выбрать масштаб по напряжению в обоих каналах таким образом, чтобы осциллограммы напряжений имели максимальный размах, не выходя за границы экрана. Если размах осциллограмм очень мал, то напряжения кажутся нулевыми и неопытный экспериментатор может не отличить неверный выбор масштаба от отсутствия переходного процесса. На рис. 7.9г настройка масштаба по напряжению на канале В исправлена. 3. Ещё одна некорректность настройки заключается в выборе слишком большой цены деле-ниия по временной оси (TIME BASE) по сравнению с постоянной времени переходного процесса. При установке по умолчанию масштаба в 0.5 с/дел весь экран соответствует времени 7.2 с, то есть =3600т (т= 2 мс). При этом масштабе получается очень крупный шаг вычисления, при котором погрешность недопустимо велика, что приводит даже к качественному изменению характера функции. Как видно из рис. 7.9г, из-за погрешности процесс изображается колебательным, что невозможно в схемах с одним реактивным элементом. На рис. 7.9д ситуация исправлена и время прохождения экрана лучом равно =7т. В общем случае необходимо стремиться к тому, чтобы время прохождения экрана лучом не превышало =20т. Проблема синхронизации осциллографа в Electronics Workbench, как и в практических измерениях, требует особого внимания. Проще всего она решается, если ключ в схеме управляется вручную. Например, на. рис. 7.5 ключ управляется при нажатии на клавишу [Space] (пробел). Если замедлить процесс расчета настолько, чтобы изображающая точка плавно "плыла" по экрану, то вы наглядно увидите развитие переходного процесса и сможете управлять ключом во время процесса. Это можно сделать, изменяя опцию Time domain points per cycle пункта Analysis Options в меню Circuit. Подробнее об этом см. Приложение 1. При получении осциллограммы рис. 7.9д была выбрана опция 1000 точек /цикл. При изменении настроек осциллографа процесс расчета продолжается, а ключ уже не управляется клавишей. Существует два способа преодоления этой трудности. Вы можете выделить ключ, щелкнув на нем мышкой (он приобретет при этом красный цвет), не прерывая процесс расчета (после этого он снова становится управляемым), а можете снова запустить расчет, активизировав схему заново. Начать получение осциллограммы переходного процесса мы рекомендуем на малой модели осциллографа, поскольку при этом можно одновременно видеть на экране и схему. Однако проводить измерения намного удобнее на расширенной модели осциллографа, появляющейся на экране после нажатия кнопки Zoom. При этом Вас не должно смущать, если на малой модели информативная часть осциллограммы уже "убежала" за экран. На расширенной модели осциллографа вы сможете снова найти ее с помощью поля прокрутки в нижней части осциллографа.
На рис. 7.10 приведена модель осциллографа после нажатия кнопки Zoom в ситуации, показанной на рис. 7.9д. При этом курсоры выставлены таким образом, чтобы нижние табло показывали начальное и установившееся значения напряжения на конденсаторе при размыкании ключа. Переведя курсор с помощью мышки в позицию максимума по каналу А, мы можем измерить ток Imp.
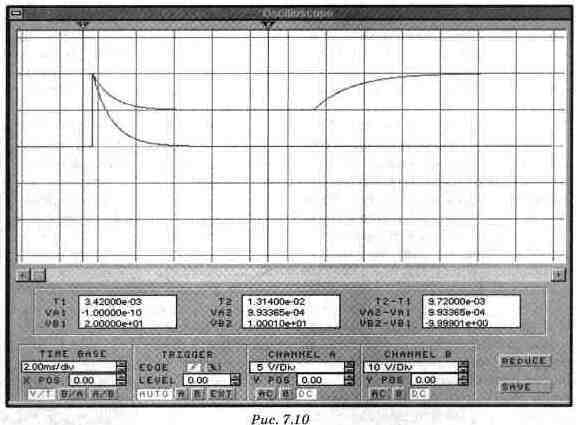
Если сдвинуть курсор 1 вправо на 1 клетку, а курсор 2 — влево на 3.5 клетки, то можно будет вычислить постоянную времени т по показаниям на табло осциллографа. Выражение для вычисления т:
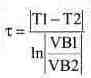
Также можно измерить начальное и установившееся значения напряжения на конденсаторе при замыкании и размыкании ключа. Переведя с помощью мыши курсор в положение максимума по каналу А, можно измерить ток Iсo. Расчетные и экспериментальные данные приведены в таблице. Таблица 7.1. Сравнение расчета с экспериментом
|
|
Замыкание ключа
|
|||
|
|
uco,B |
UcycT, В |
Ico, мА |
тЭ, МС |
|
Расчет |
10 |
20 |
0.5 |
2 |
|
Эксперимент |
10 |
20 |
0.5 |
2 |
|
|
Размыкание ключа
|
|||
|
|
UCO,B |
UсycT В |
Ico, мА |
Тр, МС |
|
Расчет |
20 |
10 |
-1.0 |
1 |
|
Эксперимент |
20 |
10 |
-1.0 |
1 |
Задача 2. Подключение конденсатора к активному двухполюснику с постоянным выходным. напряжением.
Рассчитать напряжение на конденсаторе Uc(t), ток через него ic(t) и напряжение на резисторе R3 URa(t) при замыкании и размыкании ключа [Space] в схеме рис. 7.12 (файл с7_12). Исследовать переходной процесс с помощью Electronics Workbench и сверить результаты расчета и эксперимента.
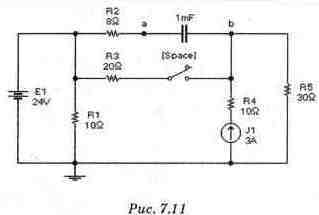
Расчет Шаг 1. Расчет Uc(t) и Ic(t). Задачу на расчет напряжения на конденсаторе и тока через него для сколь угодно сложной схемы, в которой имеется только один конденсатор и ключ на два положения, можно свести к задаче 1 данного раздела, если найти параметры эквивалентных генераторов при замкнутом и разомкнутом ключе (см. главу 2). Схема замещения при разомкнутом ключе приведена на рис. 7.12 В этом случае схема состоит из двух независимых контуров - с источником ЭДС и с источником тока. Потенциал точки "b" равен падению напряжения на резисторе R5:Ub= 30 Ом ЗА= 90 В. Потенциал точки "а" равен напряжению источника ЭДС E1 и составляет 24 В. Разность потенциалов точек а и b равна Uabp= 24 - 90= - 66 В. Для определения эквивалентного сопротивления источники ЭДС заменяются коротким замыканием, а источники тока - разрывом. Эквивалентное сопротивление Rэквр равняется при этом Rэквр=R2 +R5= 38 Ом.
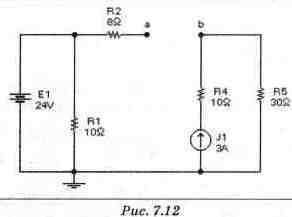
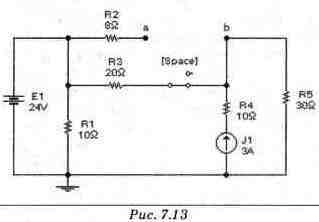
Схема замещения при замкнутом ключе представлена на рис. 7.13. Напряжение холостого хода в этом случае можно определить методом наложения. Напряжение UR3E на резисторе Rg, создаваемое источником ЭДС E1, рассчитаем по формуле делителя напряжений: UR3E= Е1Rз/(Кз+К4) = 24-20/(20+30) = 9.6 В. Напряжение UR3J, создаваемое источником тока J1 на резисторе Rз, найдем с использованием формулы делителя тока: UR3J= -J1R5R3/(R5+R5) = -3.30 20/(20+30)= -36 В.
Разность потенциалов Uabз равна сумме этих составляющих: и.ьэ= URSE + URSJ = 9.6 -36= -26.4 В. Эквивалентное сопротивление: Rэквз = R2 + RslIRs = 8 + 12 = 20 Ом. Выражение RзlIRs означает эквивалентное сопротивление для параллельного соединения Кз и Rs
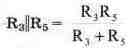
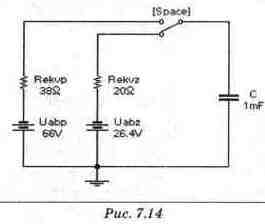
Таким образом, исходная схема сводится к схеме рис. 7.14 при вычисленных параметрах элементов. Расчет схемы рис. 7.14 проводится аналогично расчету схемы из задачи 1 данного раздела. В результате получим следующие выражения, описывающие напряжение на конденсаторе Uc(t) и ток через него ic(t) для переходного процесса при размыкании ключа:
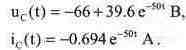
Выражения, описывающие напряжение на конденсаторе Uc(t) и ток через него ic(t) для переходного процесса при замыкании ключа:
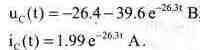
Для расчета напряжения на резисторе Rз применим стандартный алгоритм классического метода расчета переходных процессов. При замыкании ключа
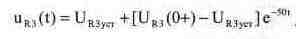
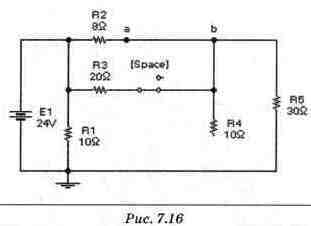
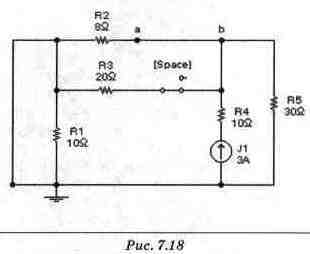
Расчет URstt). Значение URзустз нетрудно определить из схемы замещения на рис. 7.13. Однако для определения URз(0+) нам придется исследовать схему замещения для момента 0+. Исходя из условия коммутации, в исходной схеме конденсатор следует заменить источником ЭДС, напряжение которого по знаку и величине совпадает с Uc(0+). На рис. 7.15 приведена схема замещения для момента 0+ при замыкании ключа. Рассчитать процессы в этой схеме можно методом наложения, частные схемы для которого проведены на рис. 7.16, 7.17, 7.18.
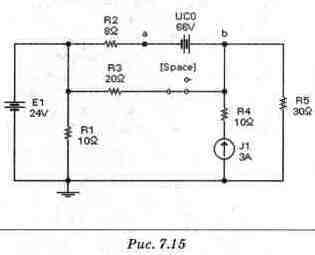
Составляющую напряжения UR3(E1) создаваемую источником ЭДС E1, определим из соотношения:
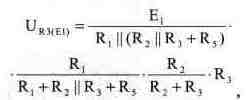
в котором первый сомножитель равен току источника ЭДС Ei, второй - коэффициенту деления делителя тока, при умножении на который мы получаем ток через сопротивление R5, третий — коэффициенту деления делителя тока, при умножении на который получается ток через сопротивление R3. При умножении на четвертый сомножитель (сопротивление R3) мы получаем напряжение URз(Е1)-Подставив в выражение значения номиналов, получим: UR3(E1) = 3.84 В. Составляющую напряжения URз(uсо), создаваемую источником ЭДС UCO, опре- • делим из соотношения:
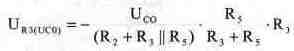
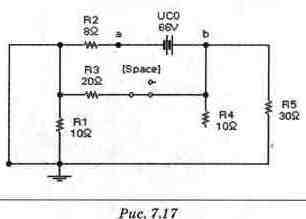
После подстановки номиналов получаем: URS(UCO) = - 39.6 В. Наконец, составляющую напряжения UR3(J1), создаваемую источником тока J1, определим из соотношения:
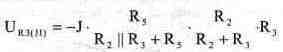
После подстановки номиналов получаем: UR3(I1) = - 14.4 В. Напряжение на резисторе Rз равно сумме составляющих напряжений, создаваемых на резисторе всеми источниками в схеме: URS= URЗ(Е1) +UR3(UCO) +UR3(Jl) В результате получаем: Uкз = - 50.16 В.
Экспериментальная проверка результатов расчета Шаг 1. Подключая мультиметр в режиме вольтметра и омметра на выходы схем замещения при разомкнутом и замкнутом ключе, проверим расчет Ераз, Езам, Rpaз и Rзaм (рис. 7.19).
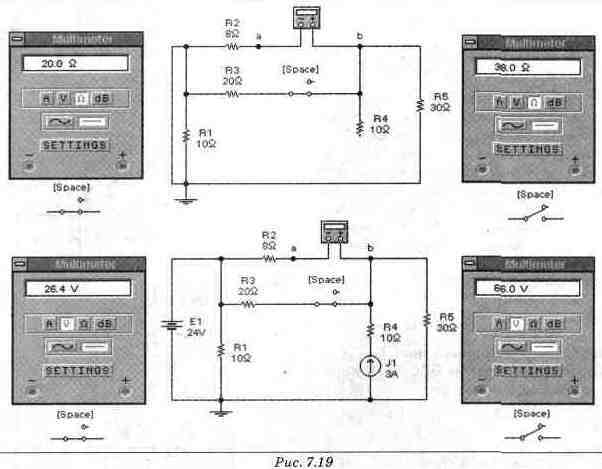
Как видно из показаний приборов на рис. 7.20, экспериментальные и расчетные данные совпадают.
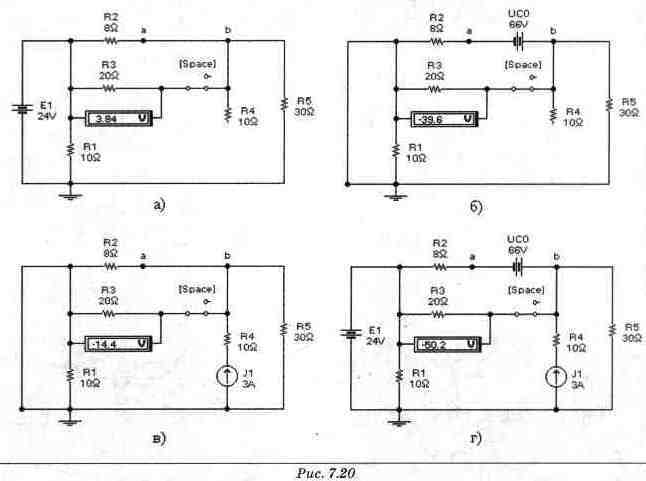
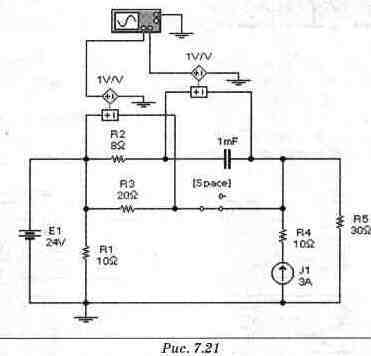
Шаг 2. На рис. 7.20(1, б, б, показано измерение составляющих напряжения на резисторе Rз, создаваемых источником ЭДС E1, источником ЭДС UCO и источником тока J1 соответственно, а на рис. 7.20г - измерение суммарного напряжения на резисторе Rз в момент времени (0+). Как видно из приведенных схем, Electronics Workbench позволяет провести пошаговую проверку расчета. Шаг 3. Подключите осциллограф, как показано нa puc. 7,21, и активизируйте схему. На экране осциллографа появятся кривые, отражающие напряжение на конденсаторе Uc и резисторе Uкз в установившемся режиме при замкнутом ключе. При размыкании ключа наблюдается переходный процесс. После того, как напряжения на обоих входах осциллографа установятся, замкнем ключ. На экране осциллографа будет наблюдаться соответствующий переходный процесс (рис. 7.22). На рис. 7.21 входы осциллографа подключены через управляемые источники ЭДС, что позволяет не заботиться о создании общей точки для двух исследуемых сигналов (см. Приложение 1). Для удобства наблюдения и управления необходимо замедлить вывод результатов эксперимента на экран. Это можно сделать, выбрав число точек на цикл равным 1000.
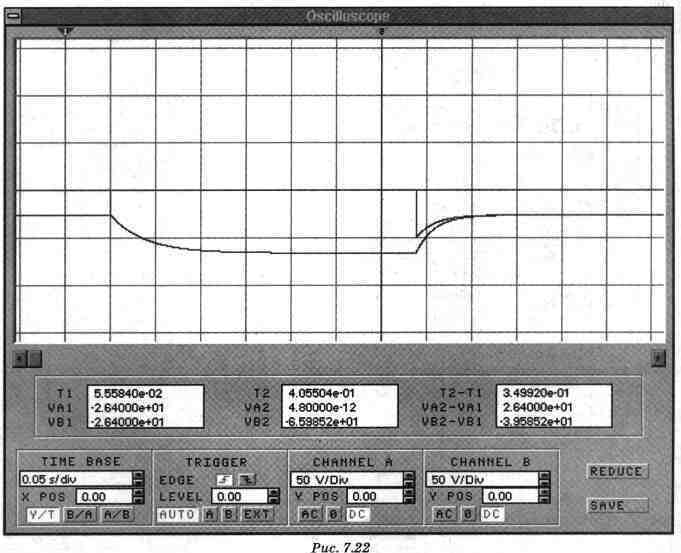
Наличие табло и курсоров позволяет использовать осциллограф как цифровой измерительный прибор мгновенных значений напряжений. Курсоры 1 и 2 на рис. 7.22 расположены таким образом, что на табло наблюдаются значения измеряемых величин в установившемся режиме (как при замкнутом, так и при разомкнутом ключе). Постоянная времени переходного процесса определяется так же, как и в задаче 1 данного раздела. В заключение приведем таблицу, в которой сравниваются результаты расчета и экспериментов. Таблица 7.2. Сравнение расчета с экспериментом
|
|
Замыкание ключа
|
|||||
|
|
Uсо, В |
UcycT,В |
ICO.A |
UR3O В |
UpSyCT, В |
Tэмс |
|
Расчет |
-26.4 |
-66 |
- 0.694 |
0 |
-50.16 |
20 |
|
Эксперимент |
-26.4 |
- 65.98 |
-0.694 |
о |
-50.2 |
20 |
|
|
Размыкание ключа
|
|||||
|
|
Uсо,B |
UcycT,В |
Iсо.A |
UR3O В |
UpSyCT В |
Тр, мс |
|
Расчет |
-66 |
-26.4 |
1.99 |
-50.16 |
о |
38 |
|
Эксперимент |
-65.98 |
-26.4 |
1.99 |
-50.2 |
о |
38 |
Задача 3. Расчет переходного процесса в цепи с одним реактивным элементом при подключении к неидеальному источнику синусоидального напряжения.
Схема в верхней части рис. 7.23 предназначена для моделирования переходного процесса в цепи с одним конденсатором. Схема в нижней части рис. 7.23 — для моделирования установившегося процесса в той же цепи. Параметры элементов в верхней и нижней части схемы идентичны. Рассчитать напряжение Uc(t), ток и ток конденсатора ic(t) при включении и выключении ключа [Space]. Переключения производить при максимуме напряжения на конденсаторе в нижней схеме рис. 7.23. Рассчитать входное напряжение таким образом, чтобы максимум установившегося напряжения был равен 100 В. Считать ключ в положении 1 включенным (замкнутым), в положении 2 - выключенным (разомкнутым). Файле? 13.са4
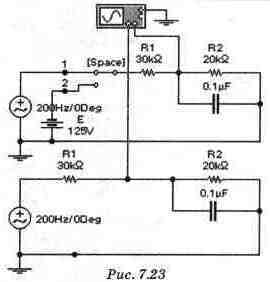
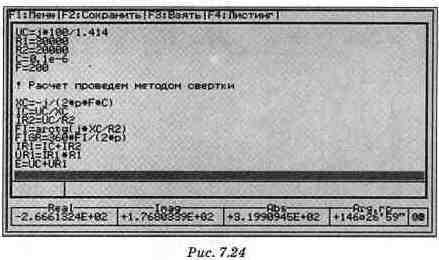
Расчет Рассмотрим сначала установившийся процесс (нижняя схема на рис. 7.23). Расчет искомого входного напряжения проведем в программе комплексного калькулятора (файл с7_13.сс). На рис. 7.24 приведено окно комплексного калькулятора с текстом программы и результатом расчета напряжения источника ЭДС. Результат расчета отображен на табло комплексного калькулятора. Напряжение источника ЭДС равно 320 В.
В схеме рис. 7.23
при разомкнутом ключе напряжения на верхнем конденсаторе Uc(0-) и Uc(0+) равны
0. Если мы замкнем ключ в момент, когда установившееся напряжение Ucycm (t)
= Uc(0-), никакого переходного процесса не будет, в схеме сразу возникнет установившийся
режим. Однако этот тривиальный случай не интересен для исследования, поэтому
выбран другой критический случай, когда отклонение ucycm (0-) от Ucycm (t) максимально.
При входном напряжении процесс при замыкании ключа отображается формулой:
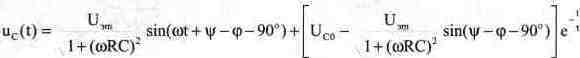
где
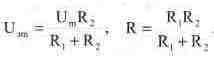
Отсчет времени ведется
от момента замыкания ключа. Если замкнуть ключ при максимуме установившегося
напряжения на конденсаторе, то угол можно определить из условия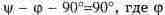 
- угол сдвига между током и напряжением источника питания. Ток конденсатора
находится из выражения:
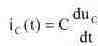
Процесс при размыкании ключа в момент максимума установившегося напряжения на конденсаторе представляет собой перезаряд конденсатора через сопротивление R от эквивалентного источника Еэ = ER2/(R1+R2) и описывается выражениями:
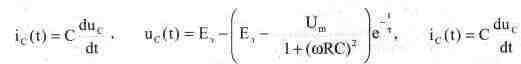
Экспериментальная проверка результатов расчета Шаг 1. Подключив осциллограф, как показано на рис. 7.24, и наблюдая на входе В установившийся процесс, переключим ключ [Space] в момент прохождения первого максимума. Получим осциллограмму напряжения на конденсаторе, являющуюся суммой свободной
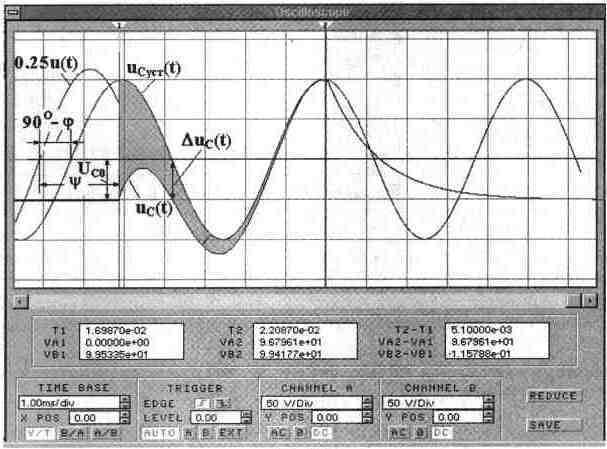
составляющей 
и составляющей установившегося
процесса, и осциллограмму установившегося процесса (рис. 7.25). Так как по условию
задачи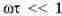 
, то к моменту про
хождения второго максимума
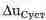будет пренебрежимо
мало. Таким образом, процесс можно считать установившимся и в это время произведем
размыкание ключа. На рис. 7.25 курсор 1 выставлен на начало переходного процесса
(момент замыкания ключа). На этот же рисунок кроме осциллограмм UcycT(t) и Uc
перенесена копированием часть уменьшенной осциллограммы питающего напряжения
0.25u(t), полученная совместно с осциллограммой Uсуст(t) в другом опыте. Это
позволяет отметить на рисунке углы, используемые в формуле 7.10 (вместо угла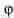
отмечен угол 
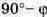). Разница между двумя измеряемыми напряжениями изменяется по экспоненте, и
найти постоянную времени в этом случае можно непосредственно по показаниям на
табло осциллографа, сместив курсор 2 на две клетки влево от положения, показанного
на рис. 7.25, и рассчитав т из выражения:
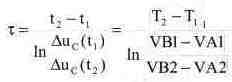
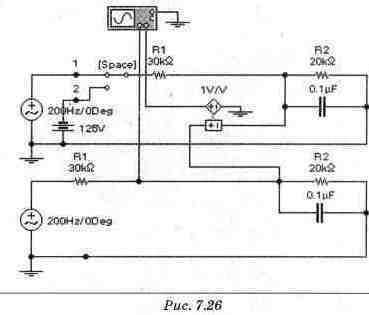
Отметим, что имеется возможность и непосредственного получения осциллограммы свободной составляющей переходного процесса при замыкании ключа, если воспользоваться датчиком напряжения в виде источника напряжения, управляемого напряжением (рис. 7.26). В этом случае постоянная времени t будет определяться формулой:
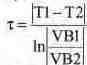
Задачи для самостоятельного решения 1. Схемы с катушкой индуктивности и одним источником
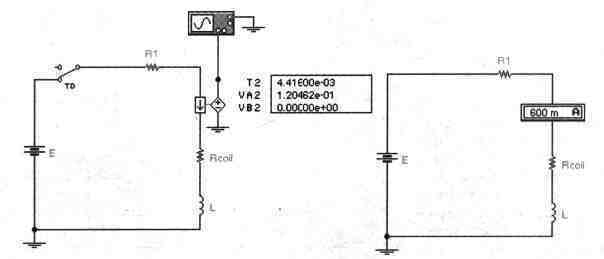
Задача 1 (с7_21) На рисунке приведены результаты эксперимента по моделированию подключения реле постоянного тока, обмотка которого имеет индуктивность 0.4 Гн и внутреннее сопротивление Rcoil =15 Ом, через дополнительное сопротивление R1 к источнику напряжения Е. Определите сопротивление R1 и величину напряжения Е. Результаты расчета проверьте с помощью Electronics Workbench.
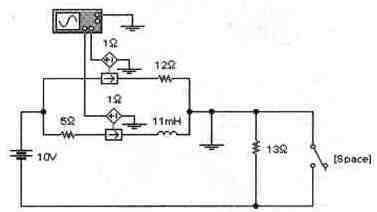
Задача 2 (с7_22) Рассчитайте токи в тех цепях, где включены датчики тока, при замыкании и размыкании ключа [Space] и постройте графики соответствующих временных зависимостей. Результаты расчета проверьте с помощью Electronics Workbench.
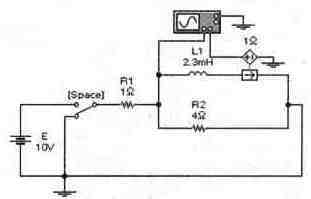
Задача 3 (с7_23) Рассчитайте временные зависимости напряжения и тока через катушку L1 при замыкании и размыкании ключа [Space] и постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
Задача 4 (с7_24) Рассчитайте временную зависимость тока через катушку L при замыкании ключа [Space] и постройте на одном графике временные зависимости тока для установившегося и переходного процессов. Замыкание и размыкание производить из установившегося процесса. Результаты расчета проверьте с помощью Electronics Workbench.
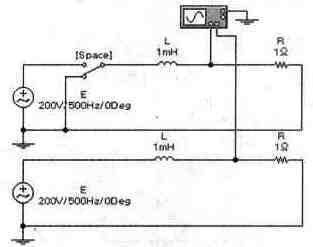
Задача 5 (с7_25) Рассчитайте временные зависимости напряжения и тока через катушку L при замыкании ключа [Space]. Постройте соответствующие графики . Результаты расчета проверьте с помощью Electronics Workbench.
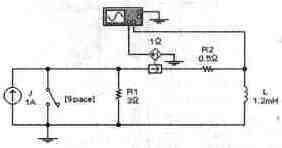
Задача 6 (с7_26) Рассчитайте временные зависимости напряжения и тока через катушку L при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
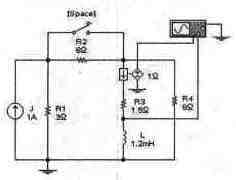
Задача 7 (с7_27) Рассчитайте временные зависимости напряжения и тока через катушку L при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
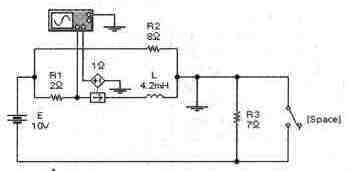
Задача 8 (с7_28) Рассчитайте временные зависимости напряжения и тока через катушку L при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
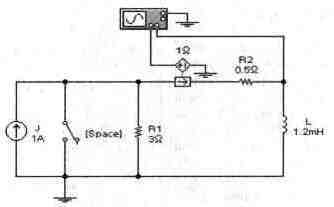
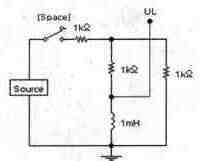
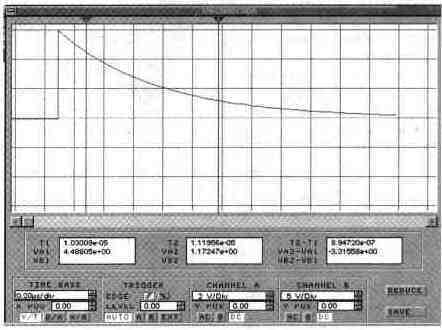
Задача 9 (с7_29) Осциллограмма напряжения на катушке получена в схеме, приведенной на рисунке слева. Определите, в какой момент получена осциллограмма (замыкания или размыкания). Является источник Source идеальным источником тока или идеальным источником напряжения? Определите величину напряжения или тока этого источника.
2. Схемы с катушкой индуктивности и двумя источниками
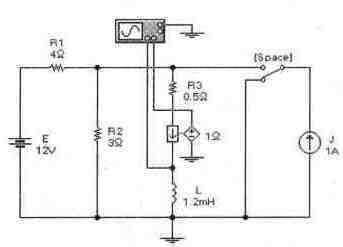
Задача 16 (с7_36) Рассчитайте временные зависимости напряжения и тока через катушку L при пере-ключениях ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
Задача 17 (с7_37) Рассчитайте временные зависимости напряжения и тока через катушку L при пере-ключениях ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
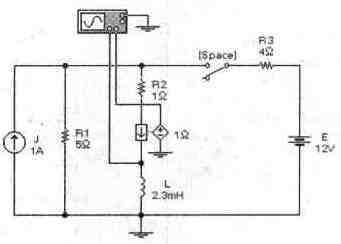
Задача 18 (с7_38) Рассчитайте временные зависимости напряжения и тока через катушку L при пере-ключениях ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
3. Схемы с конденсатором и одним источником
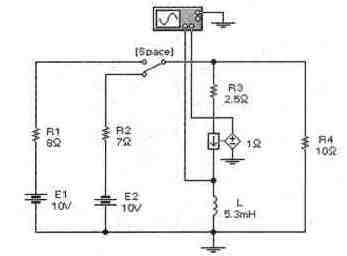
Задача 19 (с7_39) Рассчитайте временные зависимости напряжения и тока через катушку L при пере-ключениях ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
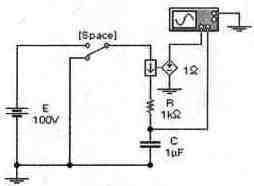
Задача 20 (с7_40) Рассчитайте временные зависимости напряжения и тока через катушку L при пере-ключениях ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
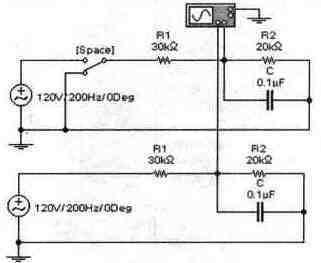
Задача 21 (с7_41) Рассчитайте временные зависимости напряжения и тока через катушку L при пере-ключениях ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
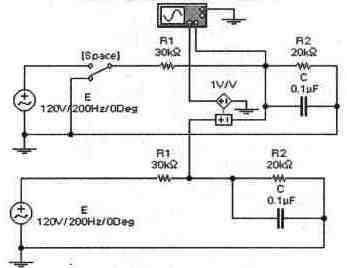
Задача 22 (с7_42) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через резистор R2 при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
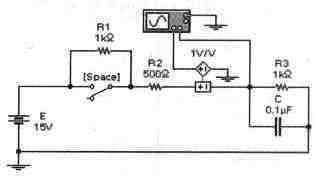
Задача 23 (с7_43) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через резистор R2 при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
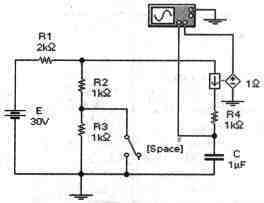
Задача 24 (с7_44) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через резистор R2 при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
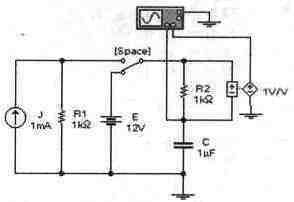
Задача 25 (с7_45) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через резистор R2 при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
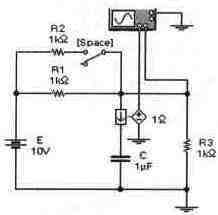
4. Схемы с конденсатором и двумя источниками
Задача 29 (с7_49) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через него при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
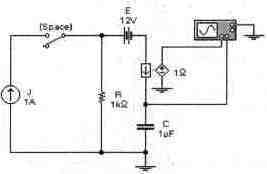
Задача 30 (с7_50) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через него при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
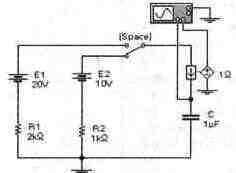
Задача 31 (с7_51) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через него при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
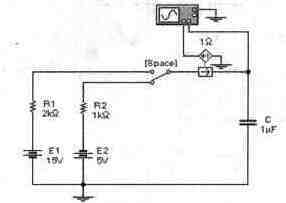
Задача 32 (с7_52) Рассчитайте временные зависимости напряжения на конденсаторе С и тока через него при замыкании ключа [Space]. Постройте соответствующие графики. Результаты расчета проверьте с помощью Electronics Workbench.
|
|
 |
