Резонанс в сложных схемах

Методические указания В этом разделе представлены упражнения по расчету и экспериментальной проверке его результатов на Electronics Workbench для цепей, находящихся в состоянии резонанса. Расчетную часть задач целесообразно выполнять с применением калькулятора комплексных чисел Comcal, описание которого приведено в приложении 2. Electronics Workbench позволяет проводить проверку результатов расчета путем соответствующих измерений. Во всех задачах мы рекомендуем строить векторные топографические диаграммы для лучшего понимания процессов при резонансе. Проверка условий резонанса для каждой из задач может быть проведена с помощью осциллографа (при этом нули тока и напряжения источника питания должны совпадать), путем измерения комплексного входного сопротивления с помощью Боде-плоттера (методика таких измерений изложена в приложении 1) или с помощью вольтметров и амперметров после построения векторной диаграммы. Задача 1. Резонанс в сложной цепи.

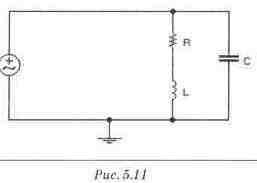
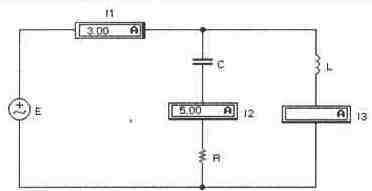
Дано: Схема рис. 5.11 при следующих параметрах элементов: Е=120 В, F= 2 кГц; R=20 Ом, L=2 мГн. Определить значение емкости конденсатора С, при котором наступает резонанс. Провести экспериментальную проверку решения с помощью Electronics Workbench. Файл с5_05.

Шаг 1. Рассчитывается комплексное сопротивление активно-индуктивной ветви.

Шаг 2. Определяется комплексная проводимость этой ветви.

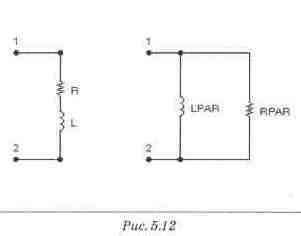
Шаг 3. Выделяются активная и реактивная составляющие комплексной проводимости и рассчитываются параметры эквивалентного двухполюсника с параллельным соединением RPAR и LPAR (схема рис. 5.13).

Шаг 4. Исходя из равенства модулей емкостного и индуктивного сопротивлений определяется необходимая емкость конденсатора. Такая методика расчета позволяет провести пошаговую проверку его правильности с использованием Electronics Workbench.

Текст из программы комплексного калькулятора с результатами

! Определить значение емкости конденсатора С, при котором наступает резонанс. !

Шаг 1. Определение комплексного сопротивления RL-цепи OREZ=FREZ*2*p ZRL=R+j*OREZ*L

! Шаг 2. Определение комплексной проводимости и ее составляющих YRL=1/ZRL BRL=(YRL - &YRL) *j/2 GRL=(YRL + &YRL)/2

! Шаг З. Определения параметров элементов в эквивалентной RL-цепи RPAR=1/GRL XPAR=1/BRL LPAR- XPAR/OREZ

Операция	Real	Imag	Abs	Arg, rp
YRL-1/ZRL	0.0194	0.0244	0.0311	-51°29'
BRL=(YBL - &YRL) *j/2	0.0244	0	0.0244	0
GRL=(YRL + &YRL)/2	0.0194	0	0.0194	0
RPAR=1/GRL	51.183	0	51.183	0
XPAR=1/BRL	41.048	0	41.048	0
LPAR= XPAR/OREZ	0.003266	0	0.003266	0

Экспериментальная проверка результатов расчета

Для экспериментальной проверки правильности вычислений следует измерить комплексные сопротивления исходного и эквивалентного двухполюсников с помощью Боде-плоттера. Измерения проводятся в схеме рис. 5.13.

Расчет Текст из программы комплексного калькулятора с результатами / Шаг 4. Определение емкости конденсатора С= 1/(OREZ*XPAR)

Операция	Real	Imag	AOS	Arg,rp
LPAR- XPAR/OREZ	1.9386-10-6	0	1.9386-10-6	0

Экспериментальная проверка результатов расчета

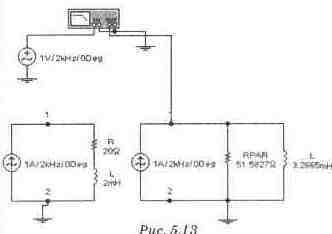
Для экспериментальной проверки правильности вычислений следует проверить условия резонанса сначала для эквивалентной схемы, а затем и для исходной. Эквивалентная схема допускает проверку условия резонанса с помощью амперметров, включенных в цепь источника питания и в цепь питания параллельного колебательного контура (рис. 5.14), При резонансе ток, ответвляемый в контур, должен быть равен 0. Как видно из рис. 5.14, он действительно близок к 0 и при токе источника питания 2.33 А составляет 54.3 мкА (0.0023%).

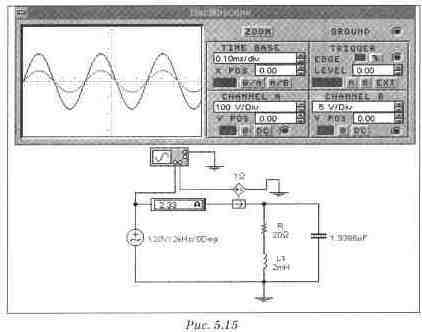
Для исходной схемы со сложным резонансом не удается отыскать ветвь, в которой резонанс прослеживался бы так явно. Поэтому следует остановиться на универсальном методе: проверить совпадение фазы питающего напряжения и питающего тока, что является общим условием резонанса для любой цепи. Наиболее наглядно такую проверку можно осуществить с помощью осциллографа в схеме рис. 5.15.

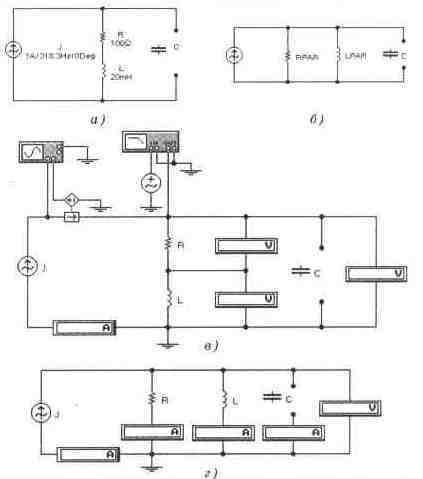
Задача 1(с5_11) Рассчитайте для схемы а) величину емкости конденсатора, при которой в схеме установится резонанс. Вычисления проведите в следующей последовательности. 1. Рассчитайте значения LPAR и RPAR в эквивалентном двухполюснике с параллельным соединением элементов (схема б)). 2. Проверьте эквивалентность схем, подсоединив вольтметры и амперметры. Какие из приборов покажут активные и реактивные составляющие входного тока и напряжения? 3. Рассчитайте емкость конденсатора, который нужно подключить к параллельной схеме г) для достижения резонанса. Проверьте расчет, подключив конденсатор через амперметр. 4. Проверьте условие выполнения резонанса с помощью осциллографа, а затем с помощью Боде-плоттера.

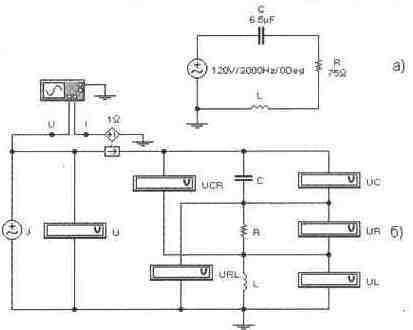
Задача 2 (с5_12) Рассчитайте для схемы величину индуктивности при резонансе. Проверьте расчет в Electronics Workbench с помощью осциллографа. Определите показания приборов в схемах при частоте w = 1000 Гц. Определите полосу пропускания контура с помощью Боде-плоттера.

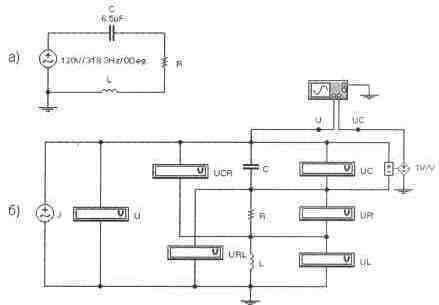
Задача 3 (с5_13) Схема на рисунке находится в резонансе. Рассчитайте сопротивление R и индуктивность L при добротности контура Q=3. Определите и проверьте экспериментально показания всех приборов в схеме б) при удвоенной резонансной частоте. Определите с помощью осциллографа угол сдвига напряжения на конденсаторе относительно напряжения источника питания на этой частоте.

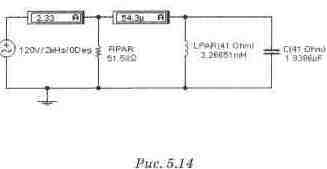
Задача 4 (с5_14) Рассчитайте значение резонансной частоты Fpeз для схемы, приведенной на рисунке. Проверьте расчет в Electronics Workbench с помощью осциллографа и Боде-плоттера. Вычислите и проверьте экспериментально показания всех приборов в схеме.

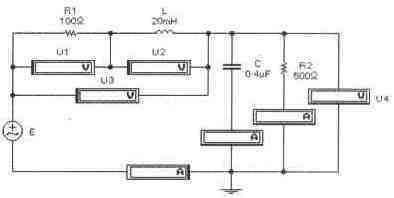
Задача 5 (с5 15) В схеме, приведенной на рис. а), имеется резонанс при частоте 50 Гц. Входное сопротивление схемы на постоянном токе составляет 5 Ом. Модуль входного сопротивления на резонансной равен 2.5 Ом. Рассчитайте величины R, Хс, XL. С и L при резонансе. Вычислите и проверьте экспериментально показания всех приборов в схеме.

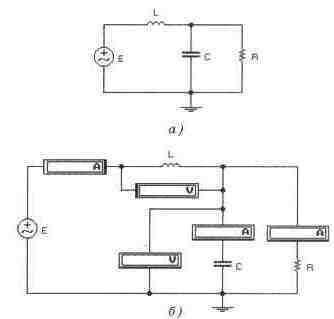
Задача 6 (с5_16) Схема, изображенная нарисунке а), находится в состоянии резонанса. Показания приборов при этом приведены на том же рисунке. Рассчитайте параметры С, L, R при резонансе. Замените последовательную ветвь R, L эквивалентным при резонансной частоте двухполюсником LPAR, RPAR, как показано на рисунке б). Каковы будут показания амперметра, не приведенные в схеме а)?

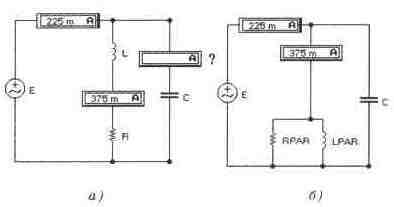
Задача 7 (с5_17) Рассчитайте резонансную частоту для схемы. Проверьте результат расчета с помощью Боде-плоттера. Вычислите и проверьте экспериментально показания приборов в схеме при резонансе. Нарисуйте (качественно) временную диаграмму изменения энергии в конденсаторе и в индуктивности при частоте большей и меньшей резонансной. Проверьте решение для энергии, применяя датчики тока, напряжения и умножители. Методика измерения энергии в катушке и конденсаторе изложена в приложении 1.

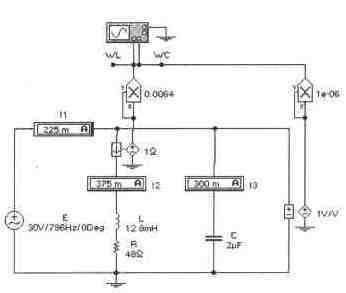
Задача 8 (с5_18) Для схемы, приведенной на рисунке, рассчитайте значение R3, при котором в схеме наступит резонанс. Проверьте выполнение условий резонанса с помощью осциллографа. Вычислите и проверьте экспериментально показания приборов в схеме.

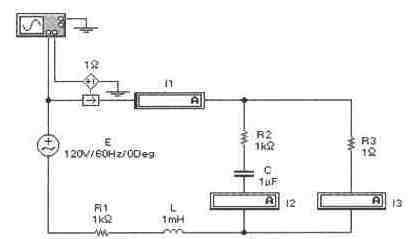
Задача 9 (с5_19) В схеме, приведенной на рисунке, наблюдается резонанс при частоте 1200 Гц. Показания приборов при резонансе приведены на схеме. Определите С и L, если R=4 Ома. Проверьте расчет экспериментально.

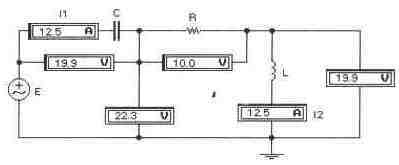
Задача 10 (с5_20) Для схемы, приведенной на рисунке, определите резонансные частоты и токи во всех ветвях схемы. Проверьте полученный результат с помощью Боде-плоттера и датчиков тока на основе зависимых источников в этих ветвях.

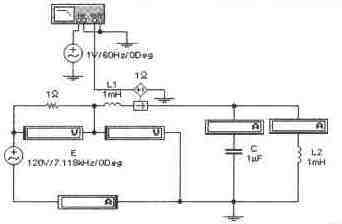
Задача 11 (с5_21) Схема, изображенная на рисунке, находится в состоянии резонанса при частоте 796 Гц, при этом мощность, потребляемая цепью, составляет Р= 1200 Вт. Показания приборов приведены на рисунке. Рассчитайте ток 12 и величины R, С, L. Проведите экспериментальную проверку.

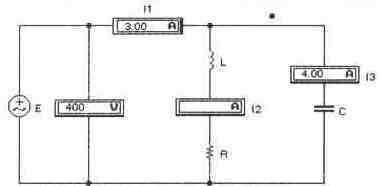
Задача 12 (с5_22) Схема находится в состоянии резонанса при частоте 796 Гц, при этом мощность, потребляемая цепью, составляет Р^1200 Вт. Показания приборов приведены на рисунке. Постройте векторную диаграмму. Рассчитайте ток 13 и величины R, С, L. Проведите экспериментальную проверку.

Знаете ли Вы, что "тёмная материя" - такая же фикция, как черная кошка в темной комнате. Это не физическая реальность, но фокус, подмена.
Реально идет речь о том, что релятивистские формулы не соответствуют астрономическим наблюдениям, давая на порядок и более меньшую массу и меньшую энергию. Отсюда сделан фокуснический вывод, что есть "темная материя" и "темная энергия", но не вывод, что релятивистские формулы не соответствуют реалиям. Подробнее читайте в FAQ по эфирной физике.