КАРОТАЖНЫЕ КАБЕЛИ
Содержание:
Введение. 13.1. Первичные электрические параметры кабелей. Активное сопротивление. Проводимость изоляции жил кабеля и электромагнитные потери. Емкость токопроводящих жил. Индуктивность кабеля. 13.2. Вторичные электрические параметры кабеля. Волновое сопротивление. Частотные характеристики жил кабеля. 13.3. Импульсный отклик кабеля. Литература.Введение
Начиная с 80-90 годов прошлого века в методах и технологиях геофизических исследований скважин (ГИС) наблюдаются существенные качественные изменения, а именно: переход на комплексные и многопараметровые измерения с применением комбинированных и/или многофункциональных скважинных приборов с достаточно глубокой обработкой первичных данных в реальном масштабе времени непосредственно в каротажных лабораториях (станциях). Такой переход требует как повышения качества первичных данных, так и передачи этих данных, как правило, в цифровой (кодовой) форме, с достаточно высокой скоростью в наземные обрабатывающие (измерительно-вычислительные) и регистрирующие устройства. И если выполнение первого требования достаточно успешно базируется на высоком уровне развития современной электронной техники, то практически единственной телеметрической линией передачи данных ГИС остается традиционный каротажный кабель.
Каротажный геофизический кабель относится к типу универсальных аналоговых кабельных линий передачи информации от скважинных приборов к каротажной станции и передачи управляющих сигналов на скважинные приборы. Пропускная информационная способность каротажного кабеля определяет скорость каротажа, особенно в комплексных методах ГИС. Однако каротажный кабель является не только электрической линией передачи информации, но и тросом с достаточно большим (до нескольких тонн) разрывным усилием, несущим скважинные приборы в химически- и механически агрессивной среде скважин. По существу, это кабель-трос специального технологического назначения, работающий в широком диапазоне температур (от минусовых на поверхности до 100-150 и более градусов на больших глубинах), что накладывает определенные ограничения на его характеристики, как линии связи. Реальная скорость передачи информации (бит/с) современных кабелей в зависимости от их длины ограничиваются диапазоном до 10-100 кГц, что начинает существенно сдерживать развитие и совершенствование технологий ГИС.
По числу токопроводящих жил (ТПЖ) каротажные кабели разделяются на три основных вида: одно-, трех- и семижильные. Как правило, кабельные каналы связи рассматриваются в рамках теории однородных длинных линий с постоянными электрическими параметрами кабеля по всей его длине. Однако в процессе каротажа различные части кабеля находятся в неодинаковых условиях давления и температуры, что приводит к изменению первичных параметров, как во времени, так и по длине кабеля. Однако, как показали исследования, изменение первичных параметров бронированных кабелей хотя и имеет место, но не столь значительно, чтобы отказаться от использования теории однородных линий.
Одножильные бронированные каротажные кабели, в принципе, относятся к разновидности коаксиальных кабелей с концентрическим расположением жилы (прямого провода) внутри брони (обратного провода). Взаимодействие электромагнитных полей прямого и обратного проводника в идеальном коаксиальном кабеле при равных значениях тока и разных его направлениях создает нулевое значение электромагнитного поля за пределами кабеля, т.е. электромагнитное поле сигналов сосредоточено внутри кабеля, что и обеспечивает эффективную передачу электромагнитной энергии с минимальными потерями. Центральная жила и оплетка коаксиальных кабелей выполняются из немагнитных материалов (медь), что также не создает потерь на перемагничивание магнитных материалов.
Каротажный кабель, в отличие от коаксиального, в качестве оплетки имеют стальную броню без поверхностной изоляции, а, следовательно, локализованного обратного тока в этой броне не существует как для одножильного, так и для многожильного кабеля. Это действительно как для кабеля на барабане лебедки, где броня представляет в какой-то мере сплошной металлический монолит, так и для кабеля в скважине, где броня – линейный заземленный электрод. Следовательно, в каротажных кабелях появляется весьма существенный источник потерь электромагнитной энергии сигналов – на перемагничивание стальной брони электромагнитными полями токопроводящих жил и межпроводниковыми электромагнитными полями (при двухпроводной передаче сигналов), а также на потери электромагнитной энергии обратного тока в окружающей среде. Эти потери нарастают с увеличением частоты тока и приводят к существенному частотному ограничению импульсной пропускной способности кабеля. Их место в математической модели кабеля подлежать уточнению.
13.1. Первичные электрические параметры кабелей [6, 7]
Активное сопротивление.
Полное активное сопротивление линии передачи сигналов кабеля состоит из суммы сопротивлений прямого и обратного проводников. Для одножильного бронированного кабеля (ОБК) и многожильного бронированного кабеля (МБК) с однопроводной линией передачи информации (МБК-1п, броня в качестве обратного проводника) сопротивление постоянному току R
0 определяется сопротивлением токопроводящей жилы (ТПЖ): длиной и конструкцией жилы, диаметром и материалом проволок жилы и температурой окружающей среды. Сопротивление обратного проводника (брони) много меньше величины сопротивления жил и его значением можно пренебречь. Для двухпроводной линии передачи (МБК-2п) полное сопротивление R0 складывается из сопротивления двух ТПЖ.Жилы кабелей свивают, в общем случае, из нескольких стренг, каждая из которых свивается из нескольких проволок. В настоящее время распространены кабели с жилами из одной стренги. Сопротивление жилы постоянному току определяется уравнением:
R0 = (rЧ L/s)Ч (m1Ч m2),
где:
r - удельное сопротивление материала проволоки при 200С в ОмЧ мм2/км, L - длина жилы в км, s - суммарная площадь всех проволок жилы в мм, m - коэффициенты скрутки проволок в стренгу и стренг в жилу. Для новых кабелей значения коэффициентов m близки к 1. С течением времени переходное сопротивление между проволоками возрастает (окисление их поверхности) и значения коэффициентов приближаются к величине 1/cos(f), где углом скрутки f учитывается длина проволок в скрутках (обычно больше длины кабеля на 10-15%). Если жилы скручиваются из медных и стальных проволок, то сопротивления для них вычисляются раздельно и затем объединяются как параллельные электрические цепи. Типовые значения r для меди и стали принимаются равными соответственно 17.5 и 98 ОмЧ мм2/км.Сопротивление жил, особенно комбинированных из стали и меди, существенно зависит от температуры. В принципе, оно может вычисляться по известному уравнению:
Rt = R20[1+m(t-20)],
где
m - температурный коэффициент (0.0039 для меди, 0.0062 для стали). Расчеты с учетом геотермического градиента по стволу скважины показывают, что при работе в скважинах с температурой до 1500С на забое сопротивление жил кабеля может увеличиваться на 10-20%. Отсюда следует, что нормальным явлением можно считать изменение сопротивления жил кабелей в процессе каротажа в пределах до 10%. Соответственно, этой величиной может ограничиваться и точность математической модели активного сопротивления жил кабеля.Активное сопротивление кабелей на высоких частотах практически прямо пропорционально корню квадратному из частоты. Это определяется так называемым поверхностным эффектом - вытеснением тока к поверхности проводов, которое возрастает с увеличением частоты, и взаимодействием полей проволок кабеля. На частотах свыше 100 кГц активное сопротивление определяется, в основном, поверхностным эффектом и в несколько раз больше сопротивления постоянному току. На частотах ниже 100 кГц эта зависимость от частоты несколько уменьшается по величине, но сохраняется по характеру. Для жил каротажного кабеля зависимость активного сопротивления от частоты дополнительно осложняется влиянием скрутки проволок в стренгу (стренг в жилу) и зависит от материала проволок (медь, сталь). Строго обоснованные аналитические методы расчетов электрических параметров многопроволочных проводников каротажных кабелей отсутствуют. С использованием известных экспериментальных данных полное активное сопротивление жилы каротажного кабеля в первом приближении может быть аппроксимировано следующими формулами:
R(f) =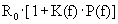 
, (13.1.1)
K(f) =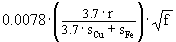 
, (13.1.1')
P(f) =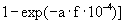 
, (13.1.1'')
где: K(f) - усредненный коэффициент поверхностного эффекта, P(f) - поправочный коэффициент для каротажного кабеля на конструкцию жилы и кабеля, r - радиус жилы в мм, s – относительные площади сечения медных и стальных проволок в жиле (s
Cu+sFe=1), a - частотная постоянная кабеля, значение которой порядка (0.1-0.3) для ОБК, ~(0.3ё 0.5) для МБК-1п, ~(0.5ё 0.8) для МБК-2п, и приближается к 1 для коаксиальных видеолиний.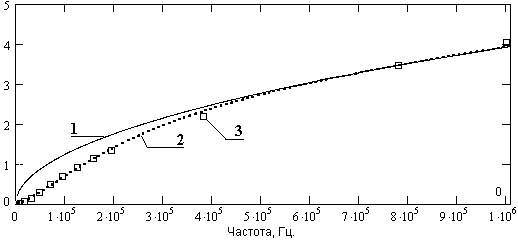
Рис. 13.1.1. Коэффициент Q(f) кабеля с медной жилой диаметром 1.05 мм
(1- коаксиальной линии, 2- расчет по формулам аппроксимации, 3- экспериментальные данные)
На рис. 13.1.1 приведено сопоставление экспериментальных данных по значению полного коэффициента Q(f) = K(f)
Ч P(f) с расчетами по формулам (13.1.1).Проводимость изоляции жил кабеля и электромагнитные потери.
Проводимость изоляции жил кабеля G определяется уравнением
G = (1/Rи) + wЧ CЧ tg(d),
где значение сопротивления изоляции R
и бронированных каротажных кабелей не менее 1000 МОм/км, а параметр d потерь на поляризацию изоляции не более 0.0005. В условиях эксплуатации значение Rи обычно поддерживается не ниже 10 МОм. Эти величины определяют проводимость изоляции жил не менее 0.0003 См/км на частотах до 1 МГц и потерями в изоляции кабелей можно пренебречь.Однако в бронированном каротажном кабеле имеют место существенные потери на перемагничивание брони и магнитных элементов окружающей среды, точное количественное значение которых предусмотреть невозможно. Влияние этих потерь на расчеты коэффициентов затухания сигнала эквивалентно потерям на поляризацию изоляции кабеля (частотно зависимая потеря энергии). Учитывая последнее, в простейшем случае можно считать возможным введение в формулу расчета проводимости дополнительного коэффициента
c - коэффициента приведения электромагнитных потерь к потерям в изоляции кабеля:G = (1/Rи) + wЧ CЧ tg(d+c ),
где значение
c для одножильных бронированных кабелей на частотах до 200 кГц порядка 0.1-0.2. Уравнение в этом случае можно считать уравнением эквивалентной проводимости кабеля, что позволяет сохранить без изменений общую теорию однородных длинных линий.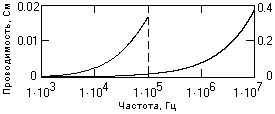
Параметр эквивалентной проводимости кабеля существенно влияет на передачу сигналов в области высоких частот. По результатам сопоставления расчетных и экспериментальных данных затухания сигнала в каротажных кабелях в диапазоне до 5 МГц может быть предложена для использования более простая формула аппроксимации эквивалентной проводимости кабеля:
G = 2pfЧ CЧ h/R(f), (13.1.2)
где значение
h порядка 12-14 для одножильных и 10-13 для многожильных кабелей. Пример расчета проводимости кабеля КГ 1х0.75-55-150 по данной формуле приведен на рис. 13.1.2.Емкость токопроводящих жил.
Емкость жил определяется конструкцией кабеля и зависит от материала и толщины изоляции ТПЖ. Для одножильных кабелей емкость ТПЖ может оцениваться по уравнению (в мкФ/км): С =
e/(18Ч ln(D/d)), где e - диэлектрическая проницаемость изоляции, D – внешний диаметр жилы по изоляции, d – диаметр токопроводника жилы. Значение емкости, как правило, находится в диапазоне 0.1-0.12 мкФ/км. Емкость между жилой и броней в многожильных кабелях имеет примерно такие же значения, а емкость жила-жила в 1.6-1.8 раз меньше. Зависимость емкостей жил от частоты практического значения не имеет. При повышении температуры емкость жил несколько уменьшается за счет уменьшения диэлектрической проницаемости изоляции, а при повышении давления – увеличивается. В скважинных условиях эти два процесса практически компенсируют друг друга и общее изменение емкости незначительно.Индуктивность кабеля.
Собственная индуктивность коаксиальных линий с увеличением частоты уменьшается вследствие поверхностного эффекта в проводах. Во внешних проводах ток вытесняется к центру кабеля, во внутренних – от центра. Соответственно, индуктивность внешних проводов уменьшается, а внутренних возрастает, но их меньший диаметр не создает полной компенсации уменьшения индуктивности внешних проводов.
Общая индуктивность пары жила-броня складывается из собственной индуктивности жилы и межпроводниковой индуктивности жила-броня. В первом приближении, для пары жила-броня из разных металлов, она может определяться с помощью уравнения, которое используется для расчетов индуктивности коаксиальных кабелей (в Гн/км):
L(f) =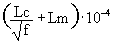 
, (13.1.3)
Lc =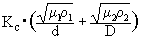 
, Kc =100/p (13.1.4)
Lm = bЧ ln(D/d), (13.1.5)
где: f - частота тока (Гц),
m - магнитные проницаемости жилы и брони (медь m1=1, сталь m2=100ё 120), r - удельные сопротивления (r1=17.5 ОмЧ мм2/км, r2=130 ОмЧ мм2/км), d – диаметр жилы (мм), D – внутренний диаметр брони кабеля, (мм), b – коэффициент учета конструкции кабеля (b » 2 для ОБК, b » 3 для МБК). Значение Lc/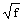
определяет собственную индуктивность жил, Lm – межпроводниковую индуктивность. Для жил, содержащих стальные проволоки в своем составе, значения m1 и 1/r1 вычисляются с учетом весовых коэффициентов площади сечений медных и стальных составляющих в общей площади сечения жилы.
Сопоставление расчетов индуктивности кабелей по формулам (13.1.3-13.1.5) с результатами экспериментальных измерений показало, что расчетные формулы завышают значения индуктивностей практически на всех частотах выше 100 Гц. По видимому, здесь играет роль, в первых, тот же фактор разницы значений прямого и обратного токов в жиле и броне (по существу – отсутствие локализованного обратного тока в броне), а во вторых, конструкция брони. Достаточно толстый двойной слой из стальных проволок с перекрестным повивом слоев не может быть эквивалентным оплетке коаксиального кабеля.
Сходимость расчетных и измеренных значений индуктивностей на частотах выше 200 Гц обеспечивается установлением в формуле (13.1.4) значения "эффективного" диаметра D
э= kЧ D кабеля вместо внутреннего диаметра брони D. Величина коэффициента k по результатам расчетных и экспериментальных значений параметров жил находится в пределах (1-1.2) для МБК-2п, (1.2-1.4) для МБК-1п и (1.4-1.6) для ОБК. В последнем случае это практически соответствует диаметру по среднему слою брони, что объяснимо по своей физической сущности. При известных значениях индуктивности жил на нескольких частотах более точная аппроксимация может производиться дополнительным изменением коэффициента Кс.Как следует из формулы (13.1.3), зависимость индуктивности от частоты определяется собственной индуктивностью жил. Она же определяет зависимость индуктивности от температуры (изменение
r). В области высоких частот индуктивность определяется, в основном, межпроводниковой индуктивностью. При намотке кабеля на лебедку его индуктивность может увеличиваться на 1-3% в зависимости от конструкции лебедки и состояния (степени окисления) поверхности брони кабеля.Межпроводниковая индуктивность многожильных кабелей для пары жила-жила увеличивается за счет индуктивности пар и влияния соседних жил. В первом приближении она может оцениваться по формуле аппроксимации экспериментальных данных:
Lm » bЧ ln((Dэ/d)+sЧ (2c/d), (13.1.6)
где с – расстояние между центрами жил, s
» (0.4-0.5) в зависимости от конструкции кабеля и определяется по измерениям индуктивности на высоких частотах.По измеренному значению индуктивности на частоте f
1 частотная функция индуктивности может вычисляться по формуле:L(f) »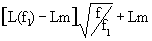 
. (13.1.7)
13.2. Вторичные электрические параметры кабелей [6,7,23]
Волновое сопротивление.
В принципе, понятие волнового сопротивления применимо только к однородным линиям, как постоянное сопротивление электромагнитной волне в любой точке кабеля при ее распространении вдоль линии любой длины. Волновое сопротивление – комплексная величина, зависимая от частоты и первичных параметров линии. В общей форме:
Z(w) =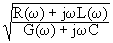 
, (13.2.1)
Если при достаточно высоком значении сопротивлении изоляции R
и в значении G пренебречь величиной 1/Rи, то это выражение можно представить в виде:Z(w) = qЧ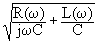 
, q =
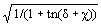» 0.93.
На частотах более 0.1 МГц отношение R(
w)/wC становится много меньше значений L(w)/C и формула упрощается:Z(w) @ qЧ 
,
при этом индуктивность жил определяется, в основном, независимой от частоты межпроводниковой индуктивностью и волновое сопротивление кабеля имеет преимущественно резистивный характер, практически не зависит от частоты, и считается номинальным волновым сопротивлением кабеля Z
в.По мере уменьшения частоты отношение R(
w)/wC увеличивается, а на частотах менее 1 кГц становится преобладающимZ(w) @ qЧ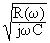 
,
т.е. содержит соизмеримые действительную и мнимую (емкостную) составляющие.
Каротажные кабели не в полной мере удовлетворяют требованиям однородных линий. Это не мешает использованию выражения (13.2.1) как в теоретическом плане, так и при чисто практических расчетах с погрешностью не более 3-5%, если специфика каротажных кабелей учитывается в функциях частотного распределения первичных параметров.
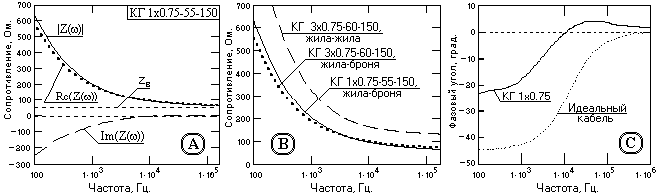
Рис. 13.2.1. Частотные характеристики волнового сопротивления реальных кабелей.
На рис. 13.2.1(A) приведены расчетные данные по волновому сопротивлению кабеля. При сравнении с идеальным кабелем можно видеть, что зависимость волнового сопротивления от частоты остается без изменения, несколько изменяются только численные значения зависимости. Волновое сопротивление жила-броня многожильных кабелей при однотипных параметрах жил и брони практически не отличается от одножильных, а для пар жила-жила отличается только увеличением числовых значений сопротивления (рис. 13.2.1(B)).
На рис. 13.2.1(С) приведено сопоставление расчетных фазочастотных характеристик волнового сопротивления реального (сплошная кривая) и идеального (нанесена пунктиром) кабеля. В целом характеристики сходны, но имеются и достаточно существенные отличия. За счет существенного возрастания значений индуктивности на низких частотах, значения и начальный интервал емкостной составляющей реального кабеля сокращаются, а на частотах выше 10 кГц в волновом сопротивлении кабеля появляется индуктивная составляющая, которая дает ощутимый фазовый сдвиг высокочастотных составляющих сигнала.
Следует ожидать, что значительная зависимость волнового сопротивления от частоты будет затруднять согласование кабеля как с наземной, так и со скважинной аппаратурой.
Частотные характеристики жил кабеля.
Характеристики коэффициента передачи сигналов по жилам кабеля, согласованным с нагрузкой по всему частотному диапазону, определяются передаточной функцией:
K(w) = ехр[-g(w)L] = exp[-(b(w)+jЧ a(w))L], (13.2.2)
где:
L – длина кабеля, g(w)L – комплексный коэффициент распространения кабеля, b(w)L – частотная характеристика затухания кабеля (собственная частотная функция затухания), a(w)L – фазочастотная функция жилы кабеля. Передаточные функции являются системными функциями кабеля, обобщающими электрические параметры его токопроводящих жил.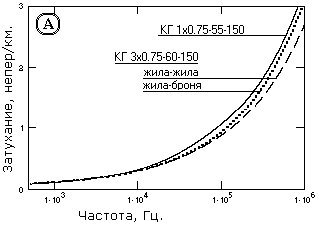
На рис. 13.2.2 приведены функции километрического затухания близких по конструкции каротажных кабелей, вычисленные с учетом реальных частотно-зависимых первичных параметров жил. Нетрудно убедиться в весьма существенном отличии затухания реального кабеля от затухания идеального кабеля, что определяется, в основном, электромагнитными потерями высокочастотной энергии в реальных кабелях. Характер частотных зависимостей на низких частотах для одно- и многожильных кабелей практически однотипный. На частотах более 10 кГц затухание одножильных кабелей несколько выше затухания многожильных, причем для последних меньшее затухание имеют пары жила-жила.
О достаточной достоверности расчетных данных можно судить по рис. 13.2.3, где приведено сопоставление расчетных значений собственного километрического коэффициента затухания одножильного бронированного кабеля с экспериментальными данными измерений коэффициента затухания сигнала на кабеле, как это принято – в неперах на 1 км, на разных частотах (нанесены точками).
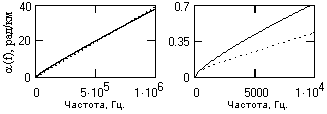
Что касается фазочастотной характеристики реального кабеля, то она практически не отличается от характеристики идеального кабеля по форме и имеет небольшие изменения числовых значений. Коэффициент фазового сдвига частотных составляющих сигнала, приведенный на рис. 13.2.4, за исключением начальной части до частоты порядка 10 кГц, остается прямо пропорциональным частоте.
Однотипность частотных характеристик одно- и многожильных кабелей позволяет в дальнейшем при рассмотрении зависимостей передаточных функций кабелей от значений различных параметров ограничиваться типичной средней частотной характеристикой жил, которая соответствует паре жила-броня многожильного кабеля.
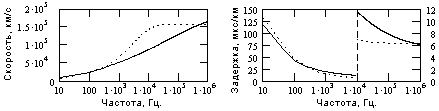
Рис. 13.2.5. Частотные функции скорости и задержки гармоник
по кабелю КГ 1х0.75-55-150 (пунктир - идеальный кабель).
Изменения фазочастотной характеристики кабеля приводят к соответствующим изменениям скорости передачи и временной задержки гармоник по кабелю без существенного изменения характера их частотной зависимости, что можно видеть на рис. 13.2.5.
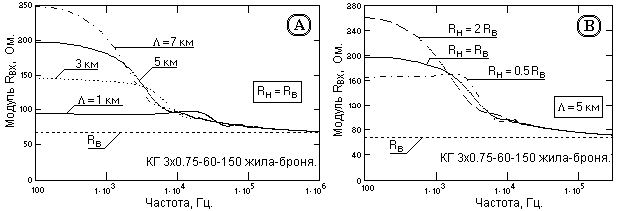
Рис. 13.2.6. Входное сопротивление кабеля.
На рис. 13.2.6 приведены расчеты по формуле (12.2.2) зависимости входного сопротивления жил от частоты при различной длине кабеля и сопротивлении нагрузки. Частотные функции модуля входного сопротивления и по форме, и по значениям, мало отличается от функций идеального кабеля (рис. 12.3.
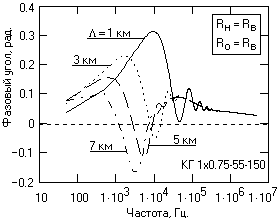
3). Изменение величины нагрузки сказывается только на изменении входного сопротивления в области частот ниже 10 кГц. Несогласованность с нагрузкой в реальном кабеле не вызывает осцилляций функций в области высоких частот, что объясняется пониженной добротностью реального кабеля.Что касается фазочастотной характеристики кабелей, пример которой приведен на рис. 13.2.7, то она по сравнению с идеальным кабелем изменяется существенно и приобретает преимущественно индуктивный характер, особенно для коротких кабелей в области средних и низких частот. Это может быть объяснено довольно существенным увеличением индуктивности реального кабеля по мере уменьшения частоты.
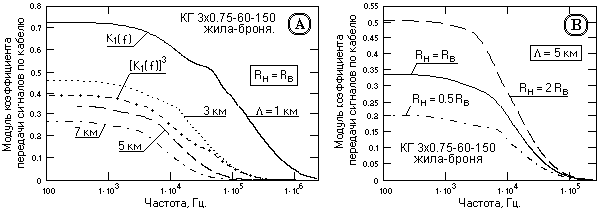
Рис. 13.2.8. Амплитудно-частотные характеристики ТПЖ кабеля.
На рис. 13.2.8 приведены графики модулей рабочих коэффициентов K
p(f) передачи сигналов по кабелю, вычисленные по формуле (12.2.1'). Сравнением с рис. 12.3.1 можно убедиться в существенном отличии амплитудных характеристик реального кабеля от аналогичных функций идеального, особенно в области высоких частот. Электромагнитные потери энергии в реальном кабеле существенно ограничивают его частотный диапазон. Влияние согласования кабеля с нагрузкой также достаточно существенно по всему частотному диапазону передачи (рис. 13.2.8(В)) и требует стабилизации ее величины при влиянии дестабилизирующих факторов.Фазочастотная характеристика кабеля практически не отличается от ФЧХ идеального кабеля и остается прямо пропорциональной значению
wL, т.е. частоте сигнала и длине кабеля, при этом коэффициент пропорциональности по своему значению несколько зависит от величины нагрузки кабеля только в области низких частот (менее 20 кГц) и только для коротких кабелей. При длине кабеля более 1.5 км его величина при изменении сопротивления нагрузки в пределах (0.5ё 2) Rв остается практически постоянной.Неполная согласованность жил кабеля с нагрузкой по частотному диапазону даже при выполнении равенства R
н = Rв проявляется в том, что не существует кабельного дискрета, который мог бы использоваться для моделирования кабеля любой длины, как линейной системы, последовательным соединением дискретов. При таком моделировании результирующий импульсный отклик кабеля на единичный входной сигнал получается путем последовательной свертки импульсных откликов кабельных дискретов, что отображается в частотной области перемножением спектров импульсных откликов дискретов. Однако, как это можно видеть на рис. 13.2.8 (А), даже при использовании достаточно длинного дискрета длиной 1 км коэффициент передачи сигнала для кабеля длиной 3 км, полученный перемножением спектров трех дискретов – [K1(f)]3, существенно отличается от коэффициента передачи, вычисленного по формуле (12.2.1'). Следовательно, реальный кабель определенной длины даже при оптимальном согласовании с нагрузкой (Rн = Rв) должен рассматриваться в виде самостоятельной системы передачи сигналов с индивидуальными для него частотными характеристиками.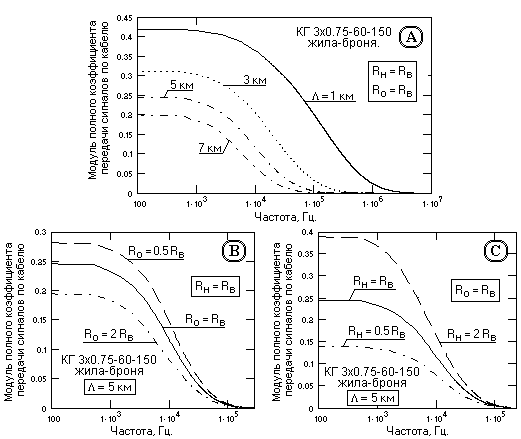
Рис. 13.2.9. Полный коэффициент передачи сигналов кабельной линией.
Формулы (12.2.1) не учитывают выходного сопротивления источника сигналов, т.е. отражают коэффициент передачи сигналов с входа линии на нагрузку при формировании (и измерении) амплитудных значений сигнала непосредственно на входе кабеля (сопротивление источника сигнала много меньше входного сопротивления кабеля на всех частотах). Расчет полного коэффициента передачи сигналов при формировании сигнала на входе источника сигналов, т.е. с учетом падения напряжения на внутреннем сопротивлении источника сигналов, выполняется по той же формуле (12.2.1) с соответствующим уточнением значения входного напряжения U
o:Uo(f) = Uc(f) Zвх(f)/(Zвх(f) + Zo), (13.2.3)
где U
c – сигнал на входе источника сигналов с внутренним сопротивлением Zo.На рис. 13.2.9 приведены графики частотной зависимости модуля полного коэффициента передачи сигналов кабельной линией от значений длины кабеля и сопротивления источников сигнала и нагрузки. Как следует из графиков, согласование кабеля с источником сигналов улучшает форму частотной характеристики и практически не изменяет относительную зависимость коэффициента передачи сигналов от частоты. Фазочастотные характеристики жил также практически не изменяются. Вместе с тем увеличивается относительная зависимость коэффициента передачи от согласования с нагрузкой. Очевидно, что только определенная стабилизация значений сопротивления нагрузки и источника сигналов от влияния дестабилизирующих факторов может гарантировать стабильность коэффициента передачи сигналов
.
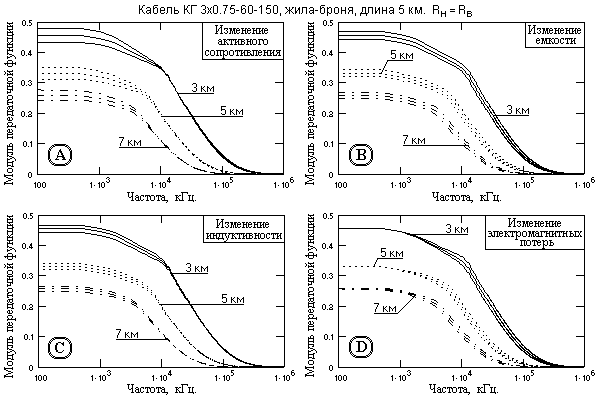
Рис. 13.2.10. Изменения амплитудно-частотной характеристики ТПЖ
при изменении ее первичных параметров в пределах
± 10%.Передаточная функция кабеля позволяет дать интегральную оценку влияния изменения первичных параметров жил на амплитудно-частотную характеристику кабеля. На рис. 13.2.10 приведены графики передаточных функций при возможных в процессе эксплуатации изменениях первичных электрических параметров жил в пределах
± 10% от номинальных.Как следует из этих графиков, на низких частотах степень чувствительности АЧХ жил кабеля порядка 0.5% на 1% изменения активного сопротивления жил, ~0.2% на 1% изменения емкости и индуктивности, и практически отсутствует при изменении электромагнитных потерь. На высоких частотах характеристики жил практически нечувствительны к изменениям активного сопротивления и индуктивности при повышении степени чувствительности к изменениям емкости и электромагнитным потерям. Учитывая, что в процессе эксплуатации изменения емкости и электромагнитных потерь много меньше изменений активного сопротивления и индуктивности (температурных и пр.) и носят, в основном, долговременный характер (старение кабеля), особое внимание следует обратить на снижение влияния активного сопротивления и индуктивности на передачу сигналов, тем более что это может достигаться уже рекомендованным методом в разделе 2: энергия сигналов должна быть минимальной в области низких частот.
Что касается устойчивости математической модели передаточных функций жил кабеля к изменению постоянных коэффициентов во всех расчетных формулах (частотная постоянная “а” в (13.1.1''), коэффициент учета конструкции кабеля “b” в (13.1.5) и пр.), то степень чувствительности передаточных функций к их изменению на порядок ниже, что свидетельствует о достаточной точности модели (не хуже 3-5% по рекомендованным средним значениям). Исключением является коэффициент электромагнитных потерь
h прямого действия, значение которого устанавливается непосредственно по передаточной функции (затуханию сигнала на высоких частотах) и приводит модель к фактическим (или паспортным) данным реального кабеля, фиксируя тем самым все возможные факторы отклонения характеристик реального кабеля от идеальной линии передачи сигналов.13.3. Импульсный отклик кабеля
Полной математической моделью кабеля в реальном масштабе времени, которой обобщаются все электрические параметры жил, является импульсный отклик жил – форма сигнала на нагрузке жилы при подаче на ее вход единичного дельта-импульса. Импульсный отклик находится обратным преобразованием Фурье частотной передаточной функции кабеля: h(t)
Ы Kp(f). Точность математической модели передаточной функции определяет соответствующую точность модели импульсного отклика жилы кабеля.
Рис. 13.3.1. Нормированные импульсные отклики кабеля.
При работе в частотном диапазоне до 1 МГц временной масштаб импульсного отклика целесообразно установить в микросекундах и вычислять отклик кабеля на единичный входной импульс U
Ч Dt = 1 (вольтЧ микросекунда), при этом масштаб значений интегрального импульсного отклика кабеля на микросекундной временной оси также будет измеряться в вольтах, а площадь импульсного отклика в (вольтЧ мкс), как и положено при прохождении импульса в пассивной линейной системе с потерями энергии, будет меньше 1.На рис. 13.3.1(А) приведены импульсные отклики кабеля, вычисленные преобразованием Фурье по функции K
p(f). Задержка tз фронта откликов (показана пунктиром) соответствует расчетному времени задержки на высоких частотах. Форма импульсного отклика жилы кабеля складывается из двух примерно экспоненциальных функций: короткой "зарядной" функции, определяющей фронт отклика, и длинной "разрядной" реакции жилы. При полном согласовании модели с электрическими параметрами жилы на интервале 0-tз не должно быть никакой реакции, что позволяет производить уточнение основных коэффициентов модели (Кс, D и h) приведением отклика на данном временном интервале к мало значимым значениям и их обнулением (при условии, что значение обнуляемой площади отклика не превышает 1-2% его полной площади). В связи с зависимостью рабочего коэффициента передачи сигнала от длины кабеля вышеописанное уточнение импульсного отклика для кабелей определенной длины, если имеется необходимость в повышении точности модели, может производиться индивидуально. Появление при расчете существенного отрицательного выброса перед фронтом импульсного отклика свидетельствует о заниженном значении коэффициентов h или эффективного диаметра D и сопровождается, как правило, занижением расчетных значений волнового сопротивления Rв относительно фактических (измеренных или среднестатистических). Ликвидацию выброса целесообразно выполнять подбором сначала коэффициента h (грубо), а затем диаметра D (точно).При Z
o Ю 0 форма собственного импульсного отклика кабеля существенно зависит от согласования с нагрузкой. Это определяется тем, что при несогласованной нагрузке отраженная от нагрузки волна полностью отражается от источника сигнала и через утроенное время задержки снова появляется на выходе кабеля, создавая второй пик на спаде отклика, положительный при Rн < Rв или отрицательный при Rн > Rв, что можно видеть на рис. 13.3.1(B) в относительных единицах от максимума отклика. Это позволяет подбором нагрузки Rн > Rв использовать повторный отрицательный пик для компенсации спада импульсного отклика и уменьшать его длительность (пример приведен на рисунке). Оптимальное согласование достигается при значении Rн порядка (1.2-1.5)Rв в зависимости от длины кабеля (при увеличении длины кабеля этот эффект уменьшается в связи с большим затуханием отраженных волн при двойном прохождении по кабелю). Для кабелей, согласованных с источником сигнала (Zo ~ Rв), эффект несогласования с нагрузкой уменьшается практически на порядок.
Рис. 13.3.2. Форма сигналов.
На рис. 13.3.2 приводятся результаты сопоставления формы импульса на нагрузке жилы кабеля при двух вариантах расчета:
1. Линейная свертка входного сигнала x(t) с импульсным откликом кабеля h(t) (свертка во временной области в дискретном варианте с интервалом дискретизации данных через 0.1 мкс):
y(t) = h(t) * x(t-t).
2. Через спектральную область (с использованием быстрого преобразования Фурье) умножением спектра сигнала на передаточную функцию кабеля (так называемая циклическая свертка):
x(t) Ю X(f). Y(f) = X(f)Ч Kр(f). Y(f) Ю y(t).
Форма сигналов практически идентична, что позволяет использовать для дальнейшего анализа и вычислений как циклическую свертку, так и оператор импульсного отклика.
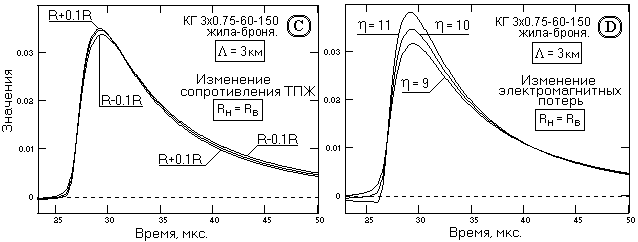
Рис. 13.3.3. Зависимость импульсных откликов ТПЖ кабеля
от изменения первичных электрических параметров.
Влияние изменения первичных электрических параметров жил на форму импульсного отклика приведено на рис. 13.3.3. Активное сопротивление жилы практически не изменяет форму отклика и несколько изменяет постоянную времени его “хвоста” за счет изменения низкочастотного состава спектра передаточной функции. Аналогично влияние изменения индуктивности жил. Более существенно изменение амплитудных значений импульсного отклика при изменении электромагнитных потерь, относительное значение изменения которых приводит к практически такому же относительному изменению амплитуды отклика (обратному по знаку), так как пиковое значение отклика формируется высокочастотными составляющими спектра передаточной функции жил. Влияние изменения емкости жил и по содержанию, и по числовым значениям практически аналогично влиянию изменения электромагнитных потерь.
Таким образом, реальный кабель представляет собой линию связи с пониженной добротностью и существенной нелинейной зависимостью передачи сигналов от длины кабеля. Каждый тип каротажного кабеля определенной длины представляет собой самостоятельную и индивидуальную систему передачи сигналов. Фактор пониженной добротности каротажных кабелей в рамках общей теории однородных длинных линий можно учитывать введением в расчетные формулы вторичных электрических параметров жил дополнительного коэффициента электромагнитных потерь.
Математические модели передаточной функции и импульсного отклика кабеля с учетом его фактических частотно-зависимых электрических параметров и пониженной добротностью отображают реальные электрические параметры кабеля с точностью не хуже 5%.
литература
6. Горбенко Л.А., Месенжник Я.З. Кабели и провода для геофизических работ. - М.: Энергия, 1977.
7. Гроднев И.И., Фролов Н.А. Коаксиальные кабели связи. - М.: Радио и связь, 1983. - 209 с.
23. Стрижевский Н.З. Коаксиальные видеолинии. – М.: Радио и связь, 1988. – 200 с.
Copyright ©2005 Davydov А.V.
Согласно релятивистской мифологии, "чёрная дыра - это область в пространстве-времени, гравитационное притяжение которой настолько велико, что покинуть её не могут даже объекты, движущиеся со скоростью света (в том числе и кванты самого света). Граница этой области называется горизонтом событий, а её характерный размер - гравитационным радиусом. В простейшем случае сферически симметричной чёрной дыры он равен радиусу Шварцшильда".
На самом деле миф о черных дырах есть порождение мифа о фотоне - пушечном ядре. Этот миф родился еще в античные времена. Математическое развитие он получил в трудах Исаака Ньютона в виде корпускулярной теории света. Корпускуле света приписывалась масса. Из этого следовало, что при высоких ускорениях свободного падения возможен поворот траектории луча света вспять, по параболе, как это происходит с пушечным ядром в гравитационном поле Земли.
Отсюда родились сказки о "радиусе Шварцшильда", "черных дырах Хокинга" и прочих безудержных фантазиях пропагандистов релятивизма.
Впрочем, эти сказки несколько древнее. В 1795 году математик Пьер Симон Лаплас писал:
"Если бы диаметр светящейся звезды с той же плотностью, что и Земля, в 250 раз превосходил бы диаметр Солнца, то вследствие притяжения звезды ни один из испущенных ею лучей не смог бы дойти до нас; следовательно, не исключено, что самые большие из светящихся тел по этой причине являются невидимыми." [цитата по Брагинский В.Б., Полнарёв А. Г. Удивительная гравитация. - М., Наука, 1985]
Однако, как выяснилось в 20-м веке, фотон не обладает массой и не может взаимодействовать с гравитационным полем как весомое вещество. Фотон - это квантованная электромагнитная волна, то есть даже не объект, а процесс. А процессы не могут иметь веса, так как они не являются вещественными объектами. Это всего-лишь движение некоторой среды. (сравните с аналогами: движение воды, движение воздуха, колебания почвы). Подробнее читайте в FAQ по эфирной физике.
|
|
 |