СТАЦИОНАРНЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ
Такова взаимосвязь: раз существует гадание, значит должны быть и боги; а раз существуют боги, значит должно быть и гадание.
Марк Туллий Цицерон. О гадании.
Римский философ и политик, I в.д.н.э.
Содержание:
Введение. 11.1. Линейные системы. Общие понятия систем. Линейные системы. Основные системные операции. Инвариантность систем к сдвигу. Математическая модель системы. Нерекурсивные цифровые системы. Рекурсивные цифровые системы. Стационарные и нестационарные системы. 11.2. Импульсная характеристика системы. Импульсный отклик системы. Реакция системы на произвольный сигнал. Усиление постоянной составляющей сигнала. Усиление шумов. Определение импульсной реакции. 11.3. Передаточные функции цифровых систем. Z-преобразование. Устойчивость систем. 11.4. Частотные характеристики систем. Основные свойства. 11.5. Реакция систем на случайные сигналы. Математическое ожидание. Корреляционные соотношения. Спектральные соотношения. Дисперсия выходного сигнала. Функция когерентности. 11.6. Структурные схемы систем. Структурные схемы. Графы систем. Соединения систем. Схемы реализации систем. Обращенные формы. Литература.введение
Преобразование и обработка сигналов осуществляется в системах. Понятия сигнала и системы неразрывны, так как любой сигнал существует в какой-либо системе его обращения. Система обработки сигналов может быть реализована как в материальной форме (специальное устройство, измерительный прибор и т.п.
), так и программно на ЭВМ или на любом другом вычислительном устройстве. Существуют и комплексные измерительно-вычислительные системы (ИВС), которые выполняют как регистрацию и первичную обработку сигналов непосредственно в материальной форме их представления, так и преобразование сигналов в цифровую форму, и последующую программную обработку. Форма реализации систем существенного значения не имеет и определяет только их возможности при анализе и обработке сигналов. Основное внимание при рассмотрении данной темы будем уделять цифровым системам и дискретной математике их отображения и анализа, применяя аналитическую математику при рассмотрении общих вопросов, если последнее упрощает изложение и понимание теоретического материала.11.1. Линейные системы [1,2,9
,14,18,20]Общие понятия систем.
Безотносительно к назначению и исполнению система всегда имеет вход, на который подается входной сигнал или входное воздействие, в общем случае многомерное, и выход, с которого снимается обработанный выходной сигнал. Если устройство системы и внутренние операции преобразований принципиального значения не имеют, то система в целом может восприниматься как “черный ящик”, в формализованном виде. Формализованная система представляет собой определенный системный оператор (алгоритм) преобразования входного сигнала – воздействия s(t), в сигнал на выходе системы y(t) – отклик или выходную реакцию системы. Символическое обозначение операции преобразования (трансформации):y(t) = T[s(t)].
Системный оператор
T - это правило (набор правил, алгоритм) преобразования сигнала s(t) в сигнал y(t). Для общеизвестных операций преобразования сигналов применяются также расширенные символы операторов трансформации, где вторым символом и специальными индексами обозначается конкретный вид операции (как, например, TF - преобразование Фурье, TF-1 - обратное преобразование Фурье).Входной сигнал системы может представлять собой m - мерный вектор (m входных сигналов), а выходной сигнал n - мерный вектор, при этом система будет иметь m входов и n выходов. Пример такой системы в геофизике: трехканальный гамма-спектрометр, на три входа решающего блока которого поступают сигналы от калиевого, радиевого и ториевого каналов спектрометра, а на три выхода выводятся сигналы содержаний калия, урана и тория, при этом системный оператор реализует алгоритм решения системы трех линейных уравнений с тремя неизвестными.
Для детерминированных входных сигналов соотношение между выходными и входными сигналами однозначно задается системным оператором. В случае реализации на входе системы случайного входного процесса также существует однозначное соответствие процессов на выходе и входе системы, однако при этом одновременно происходит изменение статистических характеристик выходного сигнала (математического ожидания, дисперсии
, корреляционной функции и пр.), которое также определяется системным оператором.Для определения системы необходимо задать характер, тип и области допустимых величин входных и выходных сигналов. Как правило, системы выполняются на сигналы одного типа по входу/выходу и подразделяются на системы непрерывного времени (аналоговые или дискретные сигналы на входе и выходе) и цифровые системы. Совокупность системного оператора Т и пространства сигналов образует математическую модель системы.
Линейные системы.
Любые преобразования сигналов сопровождаются изменением их спектра и по характеру этих изменений разделяются на два вида: линейные и нелинейные. К нелинейным относят изменения, при которых в составе спектра сигналов появляются новые гармонические составляющие. При линейных изменениях сигналов изменяются амплитуды и/или начальные фазы гармонических составляющих спектра. Оба вида изменений могут происходить как с сохранением полезной информации, так и с ее искажением. Это зависит не только от характера изменения спектра сигналов, но и от спектрального состава самой полезной информации.Линейные системы
составляют основной класс систем обработки сигналов. Термин линейности означает, что система преобразования сигналов должна иметь произвольную, но в обязательном порядке линейную связь между входным сигналом (возбуждением) и выходным сигналом (откликом). В нелинейных системах связь между входным и выходным сигналом определяется произвольным нелинейным законом.Система считается линейной, если в пределах установленной области входных и выходных сигналов ее реакция на входные сигналы аддитивна (выполняется принцип суперпозиции сигналов) и однородна (выполняется принцип пропорционального подобия).
Принцип аддитивности
требует, чтобы реакция на сумму двух входных сигналов была равна сумме реакций на каждый сигнал в отдельности:T[a(t)+b(t)] = T[a(t)]+T[b(t)].
Принцип однородности
или пропорционального подобия требует сохранения однозначности масштаба преобразования при любой амплитуде входного сигнала:T[c ґ a(t)]= c ґ T[a(t)].
Другими словами, отклик линейной системы на взвешенную сумму входных сигналов должен быть равен взвешенной сумме откликов на отдельные входные сигналы независимо от их количества и для любых весовых коэффициентов, в том числе комплексных.
Примеры.
1. Система y(t) = a2t. y(t1) = a2t1, y(t2) = a2t2, y(ct) = a2ct.
y(t1+t2) = a2(t1+t2) = a2t1+a2t2 = y(t1)+y(t2). Система аддитивна.
cy(t) = ca2t = a2ct = y(сt). Система однородна. И в целом линейна.
2. Система y(t) = at2. y(t1) = at12, y(t2) = at22, y(ct) = a(ct)2 = ac2t2.
y(t1+t2) = a(t1+t2)2 № y(t1)+y(t2)= at12+at22. Система не аддитивна.
с y(t) = с at2 № y(сt) = ac2t2. Система неоднородна. И в целом нелинейна.
При программной реализации линейных систем на ЭВМ особых затруднений с обеспечением линейности в разумных пределах значений входных и выходных сигналов, как правило, не возникает. При физической (аппаратной) реализации систем обработки данных диапазон входных и/или выходных сигналов, в котором обеспечивается линейность преобразования сигналов, всегда ограничен и должен быть специально оговорен в технической документации или методической инструкции.
Основные системные операции. К базовым линейным операциям, из которых могут быть сформированы любые линейные операторы преобразования, относятся операции скалярного умножения, сдвига и сложения сигналов:
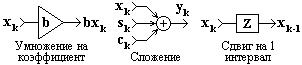
y(t) = b ґ x(t),
y(t) = x(t-Dt),
y(t) = a(t)+b(t).
Графическое отображение операций (цифровая форма) приведено на рис. 11.1.1.
Отметим, что операции сложения и умножения являются линейными только для аналоговых и дискретных сигналов. В случае цифровых сигналов они линейны относительно самих цифровых сигналов, но если последние - результат операции амплитудно-цифрового преобразования, то сложение и умножение не может считаться линейным абсолютно точно по отношению к исходным сигналам.
Для систем, с размерностью 2 и более существует также еще одна базовая операция, которая называется операцией пространственного маскирования, которая может рассматриваться как обобщение скалярного умножения. Так, для двумерных систем:
z(x,y) = c(x,y)Ч u(x,y),
где u(x,y) – двумерный входной сигнал, c(x,y) – пространственная маска постоянных (весовых) коэффициентов. Пространственное маскирование представляет собой поэлементное произведение значений сигнала с коэффициентами маски.
Инвариантность систем к сдвигу.
Система называется инвариантной к сдвигу (инвариантной во времени, а равно и по любым другим аргументам), если сдвиг входного сигнала по аргументам вызывает соответствующий сдвиг выходного сигнала:s(x,t) = T[a(x,t)], T[a(x-Dx,t-Dt)] = s(x-Dx,t-Dt).
Линейность и инвариантность к сдвигу являются независимыми свойствами систем и не определяют друг друга. Так, например, операция квадратирования сигнала (возведения в квадрат всех значений сигнала) инвариантна к сдвигу, но нелинейна.
В теории анализа и обработки данных основное место занимают системы, линейные и инвариантные к сдвигу (ЛИС - системы). Они обладают достаточно широкими практическими возможностями при относительной простоте математического аппарата. В дальнейшем, если это специально не оговаривается, будем иметь в виду именно такие системы.
Преимущество, которое отдается ЛИС - системам в методах обработки информации, базируется на возможности разложения входного сигнала любой, сколь угодно сложной формы, на составляющие простейших форм, отклик системы на которые известен и хорошо изучен, с последующим вычислением выходного сигнала в виде суммы откликов на все составляющие входного сигнала. В качестве простейших форм разложения сигналов используются, как правило, единичные импульсы и гармонические составляющие. Первая применяется при представлении сигнала в динамической форме и использует преобразование свертки, вторая - частотное представление сигнала и преобразование Фурье.
Другой важной особенностью ЛИС - систем является то, что любые их комбинации также являются ЛИС - системами, а любую сложную ЛИС - систему можно разложить на комбинации простых систем. Так, например, при последовательном (каскадном) соединении систем, когда выходной сигнал одной системы служит входным сигналом для второй и т.д., образуемая система в целом также является ЛИС - системой, если линейны и инвариантны к сдвигу все системы, в нее входящие, при этом по отношению к общей системной операции преобразования порядок соединения входящих в нее систем значения не имеет.
Математическая модель системы
задается связью между сигналами входа и выхода и в аналоговой одномерной линейной системе обычно выражается линейным дифференциальным уравнением:![]() am
am![]() =
= ![]() bn
bn![]() . (11.1.1)
. (11.1.1)
При нормировке к ао = 1, отсюда следует
:y(t) =![]() bn
bn![]() -
-![]() am
am![]() . (11.1.1')
. (11.1.1')
По существу, правой частью этого выражения в самой общей математической форме отображается содержание операции преобразования входного сигнала, т.е. задается оператор трансформации входного сигнала в выходной.
Аналогичная связь в цифровой системы описывается разностными уравнениями
:![]() am y((k-m)Dt) =
am y((k-m)Dt) = ![]() bn s((k-n)Dt). (11.1.2)
bn s((k-n)Dt). (11.1.2)
y(kDt) =![]() bn s((k-n)Dt) -
bn s((k-n)Dt) -![]() am y((k-m)Dt). (11.1.2')
am y((k-m)Dt). (11.1.2')
Последнее уравнение можно рассматривать как алгоритм последовательного вычисления значений y(k
Dt), k = 0,1,2, …, по значениям входного сигнала s(kDt) и предыдущих вычисленных значений y(kDt) при известных значениях коэффициентов am, bn и с учетом задании определенных начальных условий - значений s(kDt) и y(kDt) при k < 0. Интервал дискретизации в цифровых последовательностях отсчетов обычно принимается равным 1, т.к. выполняет только роль масштабного множителя.Нерекурсивные цифровые системы.
При нулевых значениях коэффициентов am уравнение (11.1.2') переходит в уравнение дискретной свертки x(k) с оператором bn:y(k) =![]() bn x(k-n). (11.1.3)
bn x(k-n). (11.1.3)
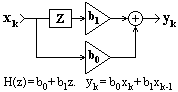
При установленных значениях коэффициентов b
n значения выходных отсчетов свертки для любого аргумента k определяются текущим и "прошлыми" значениями входных отсчетов. Такая система называется нерекурсивной цифровой системой (НЦС). Пример простейшей НЦС приведен на рис. 11.1.2. Интервал суммирования по n получил название "окна" системы. Окно системы (11.1.3) составляет N+1 точку, система является односторонней каузальной, причинно обусловленной текущими и "прошлыми" значениями входного сигнала, выходной сигнал не опережает входного. Каузальная система может быть реализована аппаратно в реальном масштабе времени. При k<n проведение обработки входных данных возможно только при задании определенных начальных условий для точек x(-k), k=1,2,..,N. Как правило, в качестве начальных условий принимаются нулевые значения или значения отсчета х(0). Применяется также четное или нечетное продление функции x(k) на интервал отрицательных значений k. Если при обработке данных начальные интервалы массивов x(k) существенного значения не имеют, то обработку можно начинать с отсчета k=N.При обработке данных на ЭВМ ограничение по каузальности системного оператора снимается. В программном распоряжении системы могут находиться как "прошлые", так и "будущие" значения входных отсчетов, при этом уравнение (11.1.3) будет иметь вид:
y(k) =![]() bn x(k-n). (11.1.3')
bn x(k-n). (11.1.3')
При N' = N система называется двусторонней симметричной. Симметричные системы, в отличие от каузальных, не изменяют фазы обрабатываемых сигналов.
Техника выполнения свертки в координатной области не отличается от техники выполнения обычной дискретной свертки двух массивов данных.
Представим, что на одной полоске бумаги выписаны по порядку сверху вниз значения данных x(k). На второй полоске бумаги находятся записанные в обратном порядке значения коэффициентов системы b
n. Для вычисления y(k) располагаем вторую полоску против первой таким образом, чтобы значение b0 совпало со значением x(k), перемножаем все значения bn с расположенными против них значениями x(k-n) и суммируем результаты перемножения. Результат суммирования является выходным значением сигнала y(k). Сдвигаем окно системы - полоску коэффициентов bk, на один отсчет последовательности x(k) вниз (по порядку возрастания номеров k) или массив x(k) сдвигаем на отсчет вверх и вычисляем аналогично следующее значение, и т.д.Описанный процесс свертки в вещественной области массива данных x(k) с нерекурсивным оператором системы b
n (массивом весовых коэффициентов системы) обычно называют нерекурсивной цифровой фильтрацией данных, а саму систему, если она выполняет только данную операцию, нерекурсивным цифровым фильтром (НЦФ).Пример. Сглаживание данных скользящим симметричным П-окном размером 5 отсчетов.
Уравнение НЦФ:
yk =Входной сигнал: x
k = {0,0,0,0,10,0,10,0,0,0,0}. Выходной сигнал: yk = {0,0,2,2,4, 4, 4,2,2,0,0}.Проверьте результат (выполните фильтрацию сигнала).
Заметим: сумма коэффициентов
bn сглаживающего НЦФ равна 1, при этом сумма значений выходного сигнала равна сумме значений входного сигнала. Сигнал "размазался" по аргументу.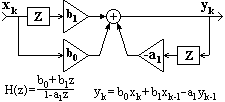
Рекурсивные цифровые системы.
Системы, которые описываются полным разностным уравнением (11.1.2), принято называть рекурсивными цифровыми системами (РЦС) или рекурсивными цифровыми фильтрами (РЦФ), так как в вычислении текущих значений выходного сигнала участвует не только входной сигнал, но и значения выходного сигнала, вычисленные в предшествующих циклах расчетов. С учетом последнего фактора рекурсивные системы называют системами с обратной связью. Пример рекурсивной системы приведен на рис. 11.1.3.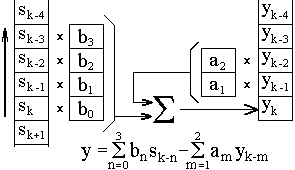
Полное окно рекурсивной системы состоит из двух составляющих: нерекурсивной части b
n,, аналогичной окну нерекурсивной системы и ограниченной в работе текущими и "прошлыми" значениями входного сигнала (при реализации на ЭВМ возможно использование и “будущих” отсчетов сигнала), и рекурсивной части am, которая работает только с "прошлыми", ранее вычисленными значениями выходного сигнала. Техника вычислений для РЦС приведена на рис. 11.1.4.Пример.
Уравнение РЦС: yk= boxk+a1yk-1, при bo=a1=0.5, y-1=0. Входной сигнал: xk = {0, 10, 0, 0, 0,....}.Расчет выходного сигнала:
у
o = 0,5xo + 0,5y-1 = 0 y1 = 0,5x1 + 0,5yo = 5 y2 = 0,5x2 + 0,5y1 = 2.5 y3 = 0,5x3 + 0,5y2 = 1.25y4 = 0,5x4 + 0,5y3 = 0.625 y5 = 0,5x5 + 0,5y4 = 0.3125 и т.д.
Выходной сигнал: yk = {0, 5, 2.5, 1.25, 0.625, 0.3125, 0.15625,...}
Из примера можно видеть, что реакция РЦС на конечный входной сигнал, в принципе, может иметь бесконечную длительность, в отличие от реакции НЦС, которая всегда ограничена количеством членов b
k (окном системы).Пример.
Уравнение РЦС: yk = boxk+a1yk-1+a2yk-2, при bo=a1=a2=1. xk = {0, 1, 0, 0, 0,....}, y-1 = y-2 = 0.Расчет выходного сигнала:
yo = xo+y-1+y-2 = 0. y1 = x1+yo+y-1 = 1. y2 = x2+y1+yo = 1. y3 = x3+y2+y1 = 2.
y4 = x4+y3+y2 = 3. y5 = x5+y4+y3 = 5. y6 = x6+y5+y4 = 8. y7 = x7+y6+y5
= 13. и т.д.Заметим: сумма коэффициентов обратной связи a
i больше 1 и выходной сигнал идет "в разнос".Пример. Интегрирование данных по формуле трапеций.
Уравнение РЦФ: y
k=(xk+xk-1)/2+yk-1, начальные условия - нулевые.Входной сигнал: x
k={0,0,2,2,8,0,4,4,0,..}.Выполните фильтрацию. Контроль: y
k= {0,0,1,3,8,12,14,18,20,20,...}.Стационарные и нестационарные системы.
Система считается стационарной и имеет постоянные параметры, если ее свойства (математический алгоритм оператора преобразования) в пределах заданной точности не зависят от входного и выходного сигналов и не изменяются ни во времени, ни от каких-либо других внешних факторов. Математически это означает задание системы уравнениями типа (11.1.1-2) с постоянными значениями коэффициентов aj и bi и реакция системы на какое-либо воздействие не зависит от времени (координат) его приложения. В противном случае система является нестационарной или параметрической (системой с переменными параметрами). Среди последних большое значение имеют так называемые адаптивные системы обработки данных. В этих системах производится, например, оценивание определенных параметров входных и выходных сигналов, по результатам сравнения которых осуществляется подстройка параметров преобразования (переходной характеристики системы) таким образом, чтобы обеспечить оптимальные по производительности условия обработки сигналов или минимизировать погрешность обработки.11.2. Импульсная характеристика системы [1,5]
Импульсный отклик системы.
По определению, импульсными характеристиками систем (второй широко используемый термин - импульсный отклик систем) называются функции h(t) для аналоговых и h(kDt) для цифровых систем, которые является реакцией (откликом) систем на единичные входные сигналы: дельта-функцию d(t) для аналоговых и импульс Кронекера d(kDt) для цифровых систем, поступающие на вход систем соответственно при t=0 и k=0. Эта реакция однозначно определяется оператором преобразования:y(t) = T[d(t)] є h(t). (11.2.1)
y(kDt) = T[d(kDt)] є h(kDt). (11.2.1')
Импульсный отклик аналоговой системы, как результат операции над дельта-функцией, в определенной степени представляет собой математическую абстракцию идеального преобразования. С практической точки зрения под импульсным откликом аналоговой системы можно понимать математическое отображение реакции системы на импульсный входной сигнал произвольной формы с площадью, равной 1, если длительность сигнала пренебрежимо мала по сравнению со временем реакции системы или с периодом ее собственных колебаний
. Под временем (длиной) реакции системы обычно понимают интервал, на котором значения функции h(t) существенно отличаются от нуля после прекращения действия единичного сигнала на ее входе.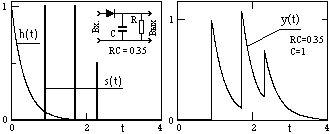
Для цифровых систем импульсный отклик однозначно определяется реакцией системы на импульс Кронекера
d(kDt)=1 при k=0.Функцию импульсного отклика называют также весовой функцией системы.
На рисунке 11.2.1 приведен пример импульсного отклика h(t) интегрирующей RC-цепи. При подаче на вход RC-цепи импульса заряда
Dq емкость С заряжается до напряжения Vо = Dq/C и начинает разряжаться через сопротивление R, при этом напряжение на ней изменяется по закону v(t) = VoЧ e-t/RC = (Dq/C)Ч e-t/RC. Отсюда, отклик RC-цепи по выходному напряжению на входной сигнал Dq = 1: h(t) = (1/C)Ч e-t/RC. По существу, импульсным откликом системы h(t) определяется доля входного сигнала, которая действует на выходе системы по истечении времени t после поступления сигнала на вход (запаздывающая реакция системы).Реакция системы на произвольный сигнал.
Если функция импульсного отклика системы известна, то, с учетом принципа суперпозиции сигналов в линейной системе, можно выполнить расчет реакции системы в любой произвольный момент времени на любое количество входных сигналов с любыми моментами времени их прихода путем суммирования запаздывающих реакций системы на эти входные сигналы, как это показано на рис. 11.2.1 для трех входных импульсов. В общем случае произвольный сигнал на входе системы может быть разложен в линейную последовательность взвешенных единичных импульсов:y(t) = T[s(t)] є T[![]() s(t)d(t-t) dt]. (11.2.2)
s(t)d(t-t) dt]. (11.2.2)
На основании принципа суперпозиции линейный оператор Т может быть внесен под знак интеграла, т.к. последний представляет собой предельное значение суммы. При этом операция преобразования действует только по переменной t:
y(t) =![]() s(t) Т[d(t-t)] dt =
s(t) Т[d(t-t)] dt =![]() s(t) h(t-t) dt. (11.2.3)
s(t) h(t-t) dt. (11.2.3)
Это выражение представляет собой интеграл Дюамеля или свертку (конволюцию) входного сигнала с импульсной характеристикой системы. Заменой переменных t-
t = t можно убедиться в том, что эта операция, как и положено свертке, коммутативна:![]() s(t) h(t-t) dt є
s(t) h(t-t) dt є ![]() h(t) s(t-t) dt.
h(t) s(t-t) dt.
Аналогично, для дискретных сигналов:
y(kDt) =![]() s(nDt) h(kDt-nDt) є
s(nDt) h(kDt-nDt) є ![]() h(nDt) s(kDt-nDt). (11.2.3')
h(nDt) s(kDt-nDt). (11.2.3')
В символической форме математического представления:
y(t) = s(t ) * h(t-t) є s(t-t) * h(t ) є s(t) * h(t).
В реальных физических системах импульсный отклик h(t) равен нулю при t<0 (реакция на выходе системы не может опережать входной сигнал) и, как правило, отличен от нуля только на определенном интервале r, по которому и ведется интегрирование или суммирование в выражениях свертки. При обработке данных на ЭВМ требований по односторонности импульсного отклика не предъявляется, равно как и по его размерам вперед и назад от нуля по координатам.
Усиление постоянной составляющей сигнала.
Подадим на вход системы постоянный сигнал s(t) = A. При этом сигнал на выходе системы:y(t) = ![]() h(t) s(t-t) dt = А
h(t) s(t-t) dt = А![]() h(t) dt = АЧ Кпс, (11.2.4)
h(t) dt = АЧ Кпс, (11.2.4)
т.е. площадь импульсного отклика (для цифровой системы соответственно сумма коэффициентов импульсного отклика) является коэффициентом К
пс усиления постоянной составляющей входного сигнала. Если при обработке сигналов должны изменяться только динамические характеристики их формы без изменения постоянной составляющей, а равно и различных постоянных уровней (фона, пьедесталов, региональных трендов и т.п.), то площадь импульсного отклика (сумма коэффициентов) должна нормироваться к единице.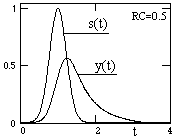
На рис. 11.2.2 приведен пример выполнения свертки рассмотренной нами выше RC-цепью при нормированной к 1 площади импульсного отклика h(
t). Входной сигнал s(t) находится на постоянном фоновом значении, в данном случае - нулевом, при этом, как и следовало ожидать, площадь выходного сигнала y(t) равна площади входного сигнала.Усиление шумов.
Критерием качества системы при использовании любого метода обработки информации можно считать выполнение целевого назначения с минимальным усилением шумов (максимальным их подавлением). Допустим, что система имеет нормированный к 1 импульсный отклик h(k). Обозначим через e(k) аддитивный шум с математическим ожиданием M{e(k)}=y(k) = ![]() h(n)[x(k-n)+e(k-n)].
h(n)[x(k-n)+e(k-n)].
Математическое ожидание значений выходного сигнала:
M{y(k)} = ![]() h(n)[x(k-n)+M{e(k-n)}] =
h(n)[x(k-n)+M{e(k-n)}] = ![]() h(n) x(k-n).
h(n) x(k-n).
Вычислим дисперсию распределения отсчетов выходного сигнала:
D{y(k)} = M{[![]() h(n)[x(k-n)+e(k-n)]-M{y(k)}]2} = M{[
h(n)[x(k-n)+e(k-n)]-M{y(k)}]2} = M{[![]() h(n) e(k-n)]2}.
h(n) e(k-n)]2}.
Если правую часть последнего выражения представить в виде
M{[![]() h(n) e(k-n)]Ч [
h(n) e(k-n)]Ч [![]() h(m) e(k-m)]},
h(m) e(k-m)]},
то в этом выражении математические ожидания всех членов произведения с сомножителями
e(n)e(m) при n № m равны 0 в силу статистической независимости значений шума. Остаются только члены с n = m, т.е.:M{![]() h2(n)e2(n)} =
h2(n)e2(n)} = ![]() h2(n) M{e2(n)} = De
h2(n) M{e2(n)} = De ![]() h2(n) = s2
h2(n) = s2![]() h2(n). (11.2.5)
h2(n). (11.2.5)
Отсюда следует, что сумма квадратов значений нормированного импульсного отклика системы представляет собой коэффициент усиления аддитивных шумов во входном сигнале.
Пример. Сглаживающий фильтр: y(k) = 0.2![]()
Коэффициент усиления шумов: 5 (0.2
2) = 0.2. Дисперсия шумов уменьшается в 1/0.2 = 5 раз.Для систем с m входами и n выходами аналогично определяются парциальные импульсные отклики h
ij(t), i = {1,2, ... ,n}, j = {1,2, ... ,m}, каждым из которых отображается сигнал на i-м выходе при поступлении сигнала d(t) на j-й вход. Полная совокупность импульсных откликов образует матрицу: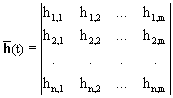 ,
,
а выражение свертки приобретает вид:
![]() =
=![]()
![]()
![]() dt.
dt.
Определение импульсной реакции
требуется, как правило, для рекурсивных систем, так как импульсная реакция для НЦС специального определения не требует:h(k) =![]() b(n)d(k-n) є b(k).
b(n)d(k-n) є b(k).
Если выражение для системы известно в общей форме (11.1.2), определение импульсной реакции производится подстановкой в уравнение системы импульса Кронекера с координатой k = 0 при нулевых начальных условиях, при этом сигнал на выходе системы будет представлять собой импульсную реакцию системы: y(k)
є h(k).Пример.
Уравнение РЦС: yk = xk + 0.5yk-1. Входной сигнал: xk= do= {1,0,0,0,...}.Расчет выходного сигнала при нулевых начальных условиях:
yo = xo+0.5 y-1 = 1+0 = 1 = ho. y1 = x1+0.5 yo = 0+0.5 = 0.5 = h1. y2 = x2+0.5 y1 = 0+0.25 = 0.25= h2
y3 = x3+0.5 y2 = 0.125 = h3. y4 = x4+0.5 y3 = 0.0625 = h4, т.д.
Импульсный отклик системы: hk = {1, 0.5, 0.25, 0.125, ... } є (O.5)k, k = 0,1,2....
Определение импульсной реакции физических систем обычно производится подачей на вход систем ступенчатой функции u
o(k) = 1 при k і 0, и uo(k) = 0 при k < 0:g(k) =![]() h(n) uo(k-n) =
h(n) uo(k-n) =![]() h(n).
h(n).
h(k) = g(k) - g(k-1), k=0,1,2,...
Функция g(k) получила название переходной характеристики системы (перехода из одного статического состояния в другое).
11.3
. Передаточные функции цифровых систем [5,18].Z-преобразование
является удобным методом решения разностных уравнений линейных систем. Применяя z-преобразование к обеим частям равенства (11.1.2), получаем:Y(z)![]() amzm = X(z)
amzm = X(z)![]() bnzn, (11.3.1)
bnzn, (11.3.1)
где X(z),Y(z)- соответствующие z-образы входного и выходного сигнала. Из этого выражения, полагая a
o = 1, получаем в общей форме функцию связи входа и выхода системы - уравнение передаточной функции системы (или системной функции) в z-области:H(z) = Y(z)/X(z) =![]() bnzn
bnzn![]() (1+
(1+![]() amzm). (11.3.2)
amzm). (11.3.2)
Для нерекурсивных систем при a
m = 0:H(z) =![]() bnzn. (11.3.3)
bnzn. (11.3.3)
При подаче на вход системы единичного импульса Кронекера
dо, имеющего z-образ d(z) = zn = 1, сигнал на выходе системы будет представлять собой импульсную реакцию системы y(k) = h(k), при этом:H(z) є Y(z) = Y(z)/d(z) = TZ[y(k)] =![]() h(k)zk, (11.3.4)
h(k)zk, (11.3.4)
т.е. передаточная функция системы является z-образом ее импульсной реакции. При обратном z-преобразовании передаточной функции соответственно получаем импульсную характеристику системы:
h(k) Ы H(z). (11.3.5)
Если функция H(z) представлена конечным степенным полиномом, как это обычно имеет место для НЦС, то обратное z-преобразование элементарно. Передаточная функция РЦС также может быть представлена степенным полиномом прямым делением числителя на знаменатель правой части выражения (11.3.2), однако результат при этом может оказаться как конечным, так и бесконечным, т.е. система может иметь либо конечную, либо бесконечную импульсную характеристику. Системы с бесконечной импульсной характеристикой получили название БИХ-систем, с конечной импульсной характеристикой соответственно КИХ-систем. Нерекурсивные системы всегда имеют конечную импульсную характеристику, т.к. длительность импульсной реакции НЦС определяется окном фильтра.
Пример. Передаточная функция рекурсивной системы: H(z) = (1-z
5)/(1-z).Делением числителя на знаменатель получаем: H(z) = 1+z+z
2+z3+z4. H(z) Ы h(n) = {1,1,1,1,1}.Система имеет конечную импульсную характеристику.
Пример. Передаточная функция: H(z)=1/(1-2z). Методом обратного преобразования: h(n) = 2
n.Система имеет бесконечную импульсную характеристику.
Устойчивость систем.
Любая практическая система должна быть устойчивой, т.е. для сигналов, конечных по энергии или средней мощности, выходные сигналы также должны быть конечными по этим параметрам. Система называется устойчивой, если при любых начальных условиях реакция системы на любое ограниченное воздействие также ограничена.Для конечного по энергии входного сигнала, можно записать:
|y(t)| Ј ![]() |h(t)||x(t-t)| dt = A
|h(t)||x(t-t)| dt = A![]() |h(t)| dt.
|h(t)| dt.
Отсюда следует условие, при котором выходной сигнал системы также будет ограниченным:
![]() |h(t)| dt < Ґ , (11.3.6)
|h(t)| dt < Ґ , (11.3.6)
т.е. необходимым и достаточным условием устойчивости системы является абсолютная сходимость ее импульсной характеристики, или, для цифровых систем, абсолютная суммируемость импульсного отклика:
![]() |h(n)| < Ґ . (11.3.6')
|h(n)| < Ґ . (11.3.6')
Анализ устойчивости может быть проведен по передаточной функции. В устойчивой системе значение H(z) должно быть конечным во всех точках z-плоскости, где |z|
Ј 1, а, следовательно, передаточная функция не должна иметь особых точек (полюсов) при z Ј 1 (на и внутри единичного круга на z-плоскости). Полюсы определяются корнями многочлена знаменателя передаточной функции H(z).Пример.
Передаточная функция РЦФ: H(z) = 1/(1+1.25z). Корни знаменателя: z = -0,8. |z| < 1.
Фильтр неустойчив.
Передаточная функция: H(z) = (1-z
3)/(1-0.6z+0.25z2). Корни: z1,2 = 1.2+1.6j. |z| = 2 > 1.Фильтр устойчив.
Приведенный критерий устойчивости относится к несократимой дроби, т.к. в противном случае возможна компенсация полюса нулем передаточной функции и следует проверить наличие однозначных нулей и полюсов.
Проверка на устойчивость требуется только для рекурсивных цифровых фильтров (систем с обратной связью), нерекурсивные системы всегда устойчивы.
11.4. Частотные характеристики систем [2,5].
Для линейных систем, принимая в качестве сигнала на входе системы собственную функцию x(k
Dt) = B(w)exp(jwkDt), мы вправе ожидать на выходе системы сигнал y(kDt) = A(w)exp(jwkDt). Подставляя эти выражения в разностное уравнение системы (11.1.2), получаем:![]() am A(w)exp(jwkDt-jwmDt) =
am A(w)exp(jwkDt-jwmDt) =![]() bn B(w)exp(jwkDt-jwnDt).
bn B(w)exp(jwkDt-jwnDt).
A(w)exp(jwkDt)![]() am exp(-jwmDt) = B(w)exp(jwkDt)
am exp(-jwmDt) = B(w)exp(jwkDt)![]() bn exp(-jwnDt).
bn exp(-jwnDt).
A(w)![]() am exp(-jwmDt) = B(w)
am exp(-jwmDt) = B(w)![]() bn exp(-jwnDt). (11.4.1)
bn exp(-jwnDt). (11.4.1)
Отсюда, частотная передаточная функция системы (частотная характеристика при нормировке к ао
=1):H(w) = A(w)/B(w) =![]() bn exp(-jwnDt)
bn exp(-jwnDt)![]() [1+
[1+![]() am exp(-jwmDt)]. (11.4.2)
am exp(-jwmDt)]. (11.4.2)
Нетрудно убедиться, что подстановкой z = exp(-j
wDt) в выражение передаточной функции H(z) (11.3.2) может быть получено абсолютно такое же выражение для частотной характеристики, т.е.:H(w) є H(z) при z = exp(-jwDt).
При обратном преобразовании H(z) во временную область с использованием выражений (11.3.4-5) отсюда следует также, что частотная характеристика системы представляет собой Фурье-образ ее импульсной реакции, и наоборот. При
Dt = 1:H(w) =![]() h(n) exp(-jwn), (11.4.3)
h(n) exp(-jwn), (11.4.3)
h(n) = (1/2p)![]() H(w) exp(jwn) dw. (11.4.4)
H(w) exp(jwn) dw. (11.4.4)
В общем случае H(
w) является комплексной функцией, модуль которой R(w) называется амплитудно-частотной характеристикой системы (АЧХ), а аргумент j(w) - фазочастотной характеристикой (ФЧХ).A(w) = |H(w)| = ![]() .
.
j
(w) = arctg(Im H(w)/Re H(w)).Физический смысл частотной характеристики системы достаточно прост. Произвольный сигнал на входе системы может рассматриваться в виде суммы гармонических составляющих с различным набором амплитуд и начальных фазовых углов. Амплитудно-частотной характеристикой системы устанавливаются коэффициенты усиления системой (коэффициенты передачи) этих частотных составляющих, а фазочастотной характеристикой - сдвиг фаз этих частотных составляющих в выходном сигнале относительно начальных фаз во входном сигнале.
Основные свойства
частотных характеристик систем:1. Частотные характеристики являются непрерывными функциями частоты.
2. При дискретизации данных по интервалам
Dt функция H(w) является периодической. Период функции H(w) равен частоте дискретизации входных данных F = 1/Dt. Первый низкочастотный период (по аргументу w от -p/Dt до p/Dt, по f от -1/2Dt до 1/2Dt) называется главным частотным диапазоном передачи сигнала. Граничные частоты главного частотного диапазона соответствуют частоте Найквиста ± wN, wN = p/Dt. Частота Найквиста определяет предел частотной разрешающей способности системы по обработке данных.3. Для систем с вещественными коэффициентами импульсной реакции h(n
Dt) функция АЧХ является четной, а функция ФЧХ - нечетной. С учетом этого частотные характеристики систем обычно задаются только на интервале положительных частот 0-wN главного частотного диапазона. Значения функций на интервале отрицательных частот являются комплексно сопряженными со значениями на интервале положительных частот.11.5. Реакция систем на случайные сигналы [2,14].
Если сигнал на входе линейной системы является детерминированным, то, при известных параметрах системы, его соотношение с выходным сигналом является однозначным. Таким же однозначным является соотношение процессов на входе и выходе и для случайных сигналов, однако в силу природы последних явное представление, как входного сигнала, так и отклика системы, не представляется возможным. Для описания отклика системы необходимо использовать статистический подход. При рассмотрении данной темы ограничимся только физически реализуемыми системами с односторонним импульсным откликом h(t) (h(t)=0 при t<0) и соответствующей частотной характеристикой H(f). Если параметры входного сигнала специально не оговариваются, то по умолчанию принимается, что на вход системы поступает реализация случайного стационарного процесса x(t) с нулевым средним и вызывает сигнал y(t) на выходе системы.
Квазидетерминированный сигнал в какой-то мере позволяет оценить сохранение однозначности преобразования системой случайных сигналов.
Допустим, что система имеет импульсный отклик h(t) = exp(-at), t і 0. Квазидетерминированный случайный сигнал стационарен, не обладает свойством эргодичности, но может быть описан в явной математической форме. Зададим сигнал на входе системы следующего вида:
x(t) = A + cos(2t+j),
где A и
j - взаимно независимые случайные величины, причем j равномерно распределена в интервале [0, 2p]. Выходной сигнал определится выражением:y(t) = h(t) * x(t-t) є ![]() h(t)Ч x(t-t) dt = A/3 + [3 cos(2t+j) + 2 sin(2t+j)]/13.
h(t)Ч x(t-t) dt = A/3 + [3 cos(2t+j) + 2 sin(2t+j)]/13.
Из выражения следует, что выходной сигнал системы также является случайным процессом и содержит те же самые случайные параметры, что и входной сигнал, а, следовательно, для него также могут быть определены статистические характеристики.
Математическое ожидание произвольного случайного стационарного сигнала x(t) на выходе линейной системы определится выражением:
![]() = М{y(t)}=
= М{y(t)}= ![]() M{x(t-t)}Ч h(t) dt =
M{x(t-t)}Ч h(t) dt =![]()
![]() h(t) dt =
h(t) dt = ![]() Кпс. (11.5.1)
Кпс. (11.5.1)
Отсюда следует, что математическое ожидание выходных сигналов системы равно математическому ожиданию входных сигналов, умноженному на коэффициент усиления системой постоянной составляющей. Если система не пропускает постоянную составляющую сигналов (площадь или сумма коэффициентов импульсного отклика системы равна нулю), то случайный выходной сигнал всегда будет иметь нулевое математическое ожидание.
Корреляционные соотношения.
Для произведения выходных сигналов y(t) и y(t+t) линейной системы можно записать:y(t)Ч y(t+t) =![]()
![]() h(a)h(b) x(t-a)x(t+t-b) da db.
h(a)h(b) x(t-a)x(t+t-b) da db.
Если взять математические ожидания от обеих частей этого равенства, то, с учетом соотношения в подынтегральном выражении
M{x(t-a) x(t+t-b)} = -Rx(t-a-t-t+b) = Rx(t+a-b),
получим:
Ry(t) =![]()
![]() h(a)h(b) Rx(t+a-b) da db є Rx(t) * h(t+a) * h(t-b). (11.5.2)
h(a)h(b) Rx(t+a-b) da db є Rx(t) * h(t+a) * h(t-b). (11.5.2)
Таким образом, функция автокорреляции (АКФ) выходного сигнала равна АКФ входного сигнала, свернутой дважды, в прямом и обратном направлении, с импульсным откликом системы, что сохраняет четность АКФ выходного сигнала. Для нецентрированных процессов аналогичное заключение действительно и для ковариационных функций.
Заметим, что для свертки импульсных откликов, производя замену t-b = t, мы имеем равенство:
h(t+a) * h(t-b) = h(t+a+b) * h(t) = h(t) * h(t+g) = Kh(t),
где K
h(t) - функция ковариации импульсного отклика системы. Отсюда:Ry(t) = Rx(t) * Kh(t). (11.5.2')
Это означает появление в случайном сигнале на выходе системы определенной корреляционной зависимости, вызванной инерционностью системы, причем радиус корреляции выходного сигнала обратно пропорционален верхней частоте, пропускаемой системой.
Для взаимной корреляционной функции (ВКФ) Rxy входного и выходного сигналов соответственно имеем:
x(t)Ч y(t+t) =![]() h(a) x(t)y(t+t-a) da.
h(a) x(t)y(t+t-a) da.
Rxy(t) =![]() h(a) Rx(t-a) da є Rx(t) * h(t-a). (11.5.3)
h(a) Rx(t-a) da є Rx(t) * h(t-a). (11.5.3)
т.е. функция взаимной корреляции входного и выходного сигналов равна свертке АКФ входного сигнала с функцией импульсного отклика системы - фильтрации АКФ сигнала этим же фильтром. Заключение действительно и для функций ковариации.
Другая взаимно корреляционная функция R
yx может быть получена из соотношения:Ryx(t) = Rxy(-t) є Rx(t) * h(t+a). (11.5.4)
Отметим, что для статистически независимых случайных величин при одностороннем импульсном отклике h(
t)=0 при t<0 функция Rxy(t) также является односторонней и равна 0 при t<0, а функция Ryx соответственно равна 0 при t>0.Спектральные соотношения, которые характеризуют систему в целом по отношению к преобразованию случайных сигналов, это соотношения частотных плотностей распределения мощности случайных процессов на входе и выходе, которые для краткости обычно называют спектральными плотностями процессов (сигналов) или спектрами мощности.
Применяя преобразование Фурье к выражениям (11.5.2), для спектра мощности выходного сигнала получаем:
Wy(f) = Wx(f) |H(f)|2. (11.5.5)
Спектр мощности сигнала на выходе системы равен спектру мощности входного сигнала, умноженному на квадрат модуля частотной характеристики фильтра. С учетом четности корреляционных функций спектр мощности выходного сигнала также является четной действительной функцией и не имеет фазовой характеристики процесса.
Аналогично, для взаимного спектра мощности на основе выражений (11.5.3-4):
Wxy(f) = Wx(f) H(f). (11.5.6)
Wyx(f) = Wx(f) H(-f).
Взаимный спектр мощности при одностороннем импульсном отклике является комплексным и содержит как амплитудную, так и фазовую характеристику процесса.
Отметим, что с использованием выражения (11.5.6) можно производить определение частотной характеристики и импульсного отклика системы:
H(f) = Wxy/Wx Ы h(t).
Дисперсия выходного сигнала
может быть определена с использованием формул (11.5.2,5):s
y2 = Ry(0) =что полностью соответствует полученной ранее формуле (11.2.5) для цифровой системы.
Если сигнал нецентрированный и значение дисперсии входного сигнала неизвестно, то по аналогичным формулам вычисляется сначала средний квадрат
выходного сигнала или так называемая средняя мощность сигнала:![]() =
=![]() = Ry(0) є
= Ry(0) є ![]()
![]() h2(t) dt є
h2(t) dt є ![]() Wx(f) |H(f)|2 df, (11.5.8)
Wx(f) |H(f)|2 df, (11.5.8)
Вывод: средняя мощность выходного сигнала равна средней мощности входного сигнала, умноженной на квадрат площади импульсной реакции системы (для цифровых систем - сумму квадратов коэффициентов импульсного отклика). Для центрированных случайных сигналов средняя мощность равна дисперсии сигналов. Для нецентрированных выходных сигналов:
s
y2 =Функция когерентности дает оценку точности принятой линейной модели системы. Когерентность входного и выходного сигналов системы оценивается по формуле:
g
xy2(f) = |Wxy(f)|2/[Wx(f)Ч Wy(f)]. (11.5.10)Если функции W
x(f) и Wy(f) отличны от нуля и не содержат дельта-функций, то для всех частот f значения функции когерентности заключены в интервале:0 Ј gxy2(f) Ј 1.
Для исключения дельта-функций на нулевой частоте (постоянная составляющая сигнала) определение функции когерентности производится по центрированным сигналам. Для линейных систем с постоянными параметрами функция когерентности равна 1, в чем нетрудно убедиться, если в формулу (11.5.10) подставить выражения W
xy и Wy, определенные через Wx в формулах (11.5.5-6). Для совершенно не связанных сигналов функция когерентности равна нулю. Промежуточные между 0 и 1 значения могут соответствовать трем ситуациям:1. Система осуществляет преобразование x(t)
Ю y(t), но в измерениях этих сигналов или одного из них присутствует внешний шум. Так, например, в сигналах, зарегистрированных с ограничением по разрядности, появляется шум квантования (округления значений).2. Система не является строго линейной. Это может наблюдаться, например, при определенном ограничении по разрядности вычислений в цифровых системах, при накоплении ошибки в рекурсивных системах и т.п.
3. Выходной сигнал y(t) помимо x(t) зависит еще от каких-то входных или внутренних системных процессов.
Величина 1-
gxy2(f) задает долю среднего квадрата сигнала y(t) на частоте f, не связанную с сигналом x(t).Использование функций когерентности в практических методах анализа случайных данных подробно рассмотрено в работе /2/.
11.6. Структурные схемы систем [5,20].
Структурные схемы.
Алгоритмы обработки сигналов в системах наглядно отображаются в виде структурных схем. Базовые элементы схем и примеры построения структурных схем приводились ранее на рис. 11.1.1-3. Как правило, структурные схемы соответствуют программной реализации систем и будут рассматриваться ниже применительно к цифровым системам, но не определяет аппаратной реализации в специальных радиотехнических устройствах, которая может существенно отличаться от программной реализации, особенно для аналоговых систем.
Графы систем.
Наряду со структурной схемой система может быть представлена в виде графа, который отображает диаграмму прохождения сигналов и состоит из направленных ветвей и узлов.Пример структурной схемы системы с передаточной функцией H(z) = (1+b
1z)/(1+a1z) и графа, ей соответствующего, приведен на рисунке 11.6.1. С каждым i узлом графа связано значение сигнала xi(k) или его образа Xi(z), которые определяются суммой всех сигналов или их z-образов входящих в узел ветвей. В каждой ij - ветви (из узла i в узел j) происходит преобразование сигнала в соответствии с передаточной функцией ветви, например, задержка сигнала или умножение на коэффициент.Соединения систем.
Различают следующие соединения систем (рис. 11.6.2-4).1. Последовательное соединение. Выходной сигнал предшествующей системы является входным для последующей. Эквивалентная передаточная функция общей системы равна произведению передаточных функций систем, в нее входящих:
H(z) = H1(z)Ч H2(z)Ч ...Ч HN(z).
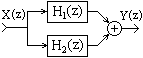
2. Параллельное соединение. Сигнал подается на входы всех параллельно соединенных систем одновременно, выходные сигналы систем суммируются. Эквивалентная передаточная функция общей системы равна сумме передаточных функций систем, в нее входящих:
H(z) = H1(z)+H2(z)+...+HN(z).
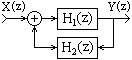
3. Соединение обратной связи. Выходной сигнал первой системы подается на выход системы и одновременно на вход системы обратной связи, выходной сигнал которой суммируется, со знаком плюс или минус в зависимости от вида связи (отрицательной или положительной), с входным сигналом первой системы. Эквивалентная передаточная функция общей системы: H(z) = H1(z)/(1± H1(z)H2(z)).
Схемы реализации систем.
По принципам структурной реализации систем различают следующие схемы: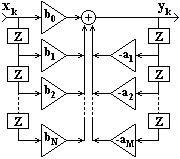
1. Прямая форма. Реализуется непосредственно по разностному уравнению
yk =![]() bnxk-n -
bnxk-n -![]() amyk-m,
amyk-m,
или по передаточной функции
H(z) =![]() bnzn /(1+
bnzn /(1+![]() amzm).
amzm).
Пример прямой системы приведен на рис
. 11.6.5.2. Прямая каноническая форма содержит минимальное число элементов задержки. Передаточную функцию РЦС можно представить в виде:
H(z) = Y(z)/X(z) = H1(z)H2(z),
H1(z) = V(z)/X(z) = 1/(1+![]() amzm), H2(z) = Y(z)/V(z) =
amzm), H2(z) = Y(z)/V(z) =![]() bnzn.
bnzn.
Отсюда:
v(k) = x(k) -![]() amv(k-m), (11.6.1)
amv(k-m), (11.6.1)
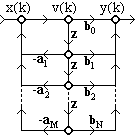
y(k) =![]() bnv(k-n). (11.6.2)
bnv(k-n). (11.6.2)
В разностных уравнениях (11.6.1-2) осуществляется только задержка сигналов v(k). Граф реализации РЦС приведен на рисунке 11.6.6.
3. Каскадная (последовательная) форма. Соответствует представлению передаточной функции в виде произведения:
H(z) =![]() Hi(z).
Hi(z).
Hi(z) - составляющие функции типа (1-riz)/(1-piz) при представлении H(z) в факторизованной форме, где ri и pi- нули и полюсы функции H(z). В качестве функций Hi(z) обычно используются передаточные функции биквадратных блоков - фильтров второго порядка:
Hi(z) = (b0i+b1iЧ z+b2iЧ z2)/(1+a1iЧ z+a2iЧ z2).
4. Параллельная форма. Используется много реже и соответствует представлению передаточной функции в виде суммы биквадратных блоков или более простых функций.

Обращенные формы.
В теории линейных сигнальных графов существуют процедуры преобразования исходных графов с сохранением передаточных функций. Одна из таких процедур - обращение графов, которое выполняется путем изменения направления всех ветвей цепи, при этом вход и выход графа также меняются местами. Для ряда систем такая транспозиция позволяет реализовать более эффективные алгоритмы обработки данных. Пример обращения графа прямой канонической формы рекурсивной системы (с перестроением на расположение входа с левой стороны) приведен на рис. 11.6.7.литература
1. Баскаков С.И. Радиотехнические цепи и сигналы
: Учебник для вузов. - М.: Высшая школа, 1988.2. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. – М.: Мир, 1989. – 540 с.
5. Гольденберг Л.М. и др. Цифровая обработка сигналов: Учебное пособие для вузов. - М.: Радио и связь, 1990.- 256 с.
9. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. – М.: Мир, 1988. – 488 с.
14. Купер Дж., Макгиллем А. Вероятностные методы анализа сигналов и систем. – М.: Мир, 1989.
18. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. – М.: Связь, 1979. – 416 с.
20. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. – М.: Мир, 1978.
Copyright ©2005 Davydov А.V.
|
|
